神经网络的快速介绍
人工神经网络(ANN)是一种计算模型,受到人脑过程信息生物神经网络的启发。人造神经网络在机器学习研究和行业中引起了极大兴奋,这得益于语音识别,计算机视觉和文本处理方面的许多突破性成果。在这篇博文中,我们将尝试开发对称为多层感知器的特定类型人造神经网络的理解。
单神经元
神经网络中的基本计算单位是神经元,通常称为节点或单位。它从一些其他节点或外部源接收输入并计算输出。每个输入具有相关联的权重(w),其基于其对其他输入的相对重要性而被分配。节点将函数f(定义如下)应用于其输入的加权和,如下图1所示:
![]()
图1:单个神经元
上述网络采用数字输入X1和X2,并具有与这些输入相关联的权重w1和w2。另外,还有另一个输入1,其重量b(称为偏置)与其相关联。我们将在稍后了解有关偏见的作用的更多细节。
如图1所示计算来自神经元的输出Y。函数f是非线性的,称为激活函数。激活功能的目的是将非线性引入神经元的输出。这很重要,因为大多数现实世界的数据是非线性的,我们希望神经元学习这些非线性表示。
每个激活函数(或非线性)都采用单个数字,并对其执行一定的固定数学运算[2]。在实践中可能会遇到几种激活功能:
- Sigmoid: 取实值输入并将其压缩到0到1之间
σ(x)= 1 /(1 + exp(-x))
- tanh:取实数输入并将其压缩到范围[-1,1]
tanh(x)=2σ(2x)-1
- ReLU:ReLU代表整流线性单元。它需要实值输入并将其设置为零(将负值替换为零)
f(x)= max(0,x)
下面的图[2]显示了上述每个激活功能。
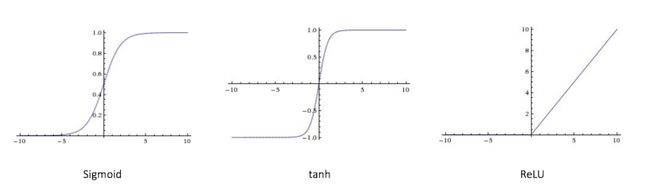 图2:不同的激活功能
图2:不同的激活功能
偏见的重要性:偏差的主要功能是为每个节点提供可训练的常数值(除了节点接收的正常输入之外)。请参阅此链接,以了解有关神经元偏见的作用的更多信息。
前馈神经网络
前馈神经网络是第一种也是最简单的人造神经网络[3]。它包含多个排列成层次的神经元(节点)。来自相邻层的节点在它们之间具有连接或边缘。所有这些连接都具有与它们相关的权重。
前馈神经网络的一个例子如图3所示。
![]()
图3:前馈神经网络的一个例子
前馈神经网络可以由三种类型的节点组成:
- 输入节点 - 输入节点向外部网络提供信息,并称为“输入层”。在任何Input节点中不执行计算 - 它们只将信息传递给隐藏节点。
- 隐藏节点 - 隐藏节点与外界无直接联系(因此名称为“隐藏”)。它们执行计算并将信息从输入节点传送到输出节点。隐藏节点的集合形成“隐藏层”。而前馈网络只能有一个输入层和一个输出层,它可以有零个或多个隐藏层。
- 输出节点 - 输出节点统称为“输出层”,负责从网络到外界的计算和传输信息。
在前馈网络中,信息仅在一个方向上移动 - 从输入节点向前移动,通过隐藏节点(如果有的话)和输出节点。网络中没有周期或循环[3](前馈网络的这种特性不同于循环神经网络,其中节点之间的连接形成一个周期)。
以下给出了前馈网络的两个示例:
-
单层感知器 - 这是最简单的前馈神经网络[4],不包含任何隐藏层。您可以在[4],[5],[6],[7]中了解更多有关单层感知器的信息。
-
多层感知器 - 多层感知器具有一个或多个隐藏层。我们将仅讨论下面的多层感知器,因为它们比当今实际应用中的单层感知器更有用。
多层感知器
多层感知器(MLP)包含一个或多个隐藏层(除了一个输入层和一个输出层之外)。虽然单层感知器只能学习线性函数,但多层感知器也可以学习非线性函数。
图4显示了具有单个隐藏层的多层感知器。注意,所有连接都具有与它们相关联的权重,但是在图中仅示出三个权重(w0,w1,w2)。
输入层:输入层有三个节点。偏置节点的值为1.另外两个节点将X1和X2作为外部输入(这是取决于输入数据集的数值)。如上所述,在输入层中不执行计算,因此输入层中的节点的输出分别为1,X1和X2,馈入隐层。
隐层: 隐层也有三个节点,Bias节点的输出为1.隐层中的另外两个节点的输出取决于输入层(1,X1,X2)的输出以及与连接(边缘)相关联的重量。图4显示了其中一个隐藏节点(突出显示)的输出计算。类似地,可以计算来自其他隐藏节点的输出。记住f是指激活功能。然后将这些输出馈送到输出层中的节点
![]()
图4:具有一个隐层的多层感知器
输出层:输出层有两个节点,它们从隐藏层获取输入,并对突出显示的隐藏节点执行类似的计算。作为这些计算的结果计算出的值(Y1和Y2)用作多层感知器的输出。
给定一组特征X =(x1,x2,...) 和目标y,多层感知器可以了解特征和目标之间的关系,用于分类或回归。
让我们举个例子来更好地了解多层感知器。假设我们有以下学生标记数据集:
![]()
两个输入列显示学生学习的小时数和学生获得的中期标记。最终结果列可以有两个值1或0,表示学生是否在最终期限内通过。例如,我们可以看到,如果学生在中期学习了35个小时,获得了67分,他/她终于通过了最后一个任期。
现在,假设我们想预测一个在中期学习25小时并有70分的学生是否会通过最后一个学期。
![]()
这是一个二分类问题,其中多层感知器可以从给定的示例(训练数据)中学习,并给出新的数据点的知情预测。下面我们将看到多层感知器如何学习这种关系。
培训我们的MLP:反向传播算法
多层感知器学习的过程称为反向传播算法。我会推荐阅读这个Quora的回答由Hemanth Kumar(引用如下),这反映了反向传播。
错误的向后传播,通常缩写为BackProp是可以训练人造神经网络(ANN)的几种方式之一。它是一个监督的培训计划,这意味着它从标记的培训数据(有一个主管,指导其学习)学习。
简单来说,BackProp就像“从错误中学习”。主管当错误地纠正ANN。
ANN由不同层的节点组成;输入层,中间隐藏层和输出层。相邻层的节点之间的连接具有与它们相关联的“权重”。学习的目的是为这些边缘分配正确的权重。给定输入向量,这些权重确定输出向量是什么。
在监督学习中,训练集被标注。这意味着,对于某些给定的输入,我们知道所需/期望的输出(标签)。
BackProp算法:
最初所有边缘权重都是随机分配的。对于训练数据集中的每个输入,ANN被激活并且观察其输出。将此输出与我们已经知道的所需输出进行比较,并将错误“传播”回上一层。该错误被注明,权重相应地“调整”。重复该过程,直到输出误差低于预定阈值。一旦上述算法终止,我们就有一个“学习”的ANN,我们认为它们已经准备好使用“新的”输入。据说这个ANN从几个例子(标记数据)和错误(错误传播)中学到了。
现在我们了解Backpropagation如何工作,让我们回到上面显示的学生标记数据集。
图5所示的多层感知器(改编自Sebastian Raschka 对反向传播算法的出色视觉解释)在输入层(除偏倚节点之外)中有两个节点,它们输入“小时研究”和“中期标记”。它还具有一个带有两个节点(除了Bias节点之外)的隐藏层。输出层也有两个节点 - 上层节点输出“Pass”的概率,而下层节点输出“Fail”的概率。
在分类任务中,我们通常使用Softmax函数作为多层感知器输出层中的激活函数,以确保输出是概率,它们加起来为1. Softmax函数采用任意实值分数向量,将它压缩到零和一之间的值向量,总和为1。所以在这种情况下,
概率(通过)+概率(失败)= 1
步骤1:正向传播
网络中的所有权重都被随机分配。让我们考虑 下面图5中标记为V的隐藏层节点。假设从输入到该节点的连接的权重为w1,w2和w3(如图所示)。
然后,网络将第一个训练示例作为输入(我们知道,对于输入35和67,通过的概率为1)。
- 输入到网络= [35,67]
- 来自网络的所需输出(目标)= [1,0]
那么考虑到节点输出V可以如下计算(f是一个激活函数,如sigmoid):
V = f (1 * w1 + 35 * w2 + 67 * w3)
类似地,还计算隐层中另一节点的输出。隐层中的两个节点的输出充当输出层中两个节点的输入。这使我们能够计算输出层中两个节点的输出概率。
假设输出层中两个节点的输出概率分别为0.4和0.6(由于权重是随机分配的,输出也将是随机的)。我们可以看出,所计算的概率(0.4和0.6)与期望的概率(分别为1和0)非常远,因此图5中的网络被称为具有“不正确的输出”。
![]()
图5:多层感知器中的正向传播步骤
步骤2:反向传播和权重更新
我们计算输出节点的总误差,并通过反向传播通过网络传播这些错误来计算梯度。然后,我们使用一种优化方法诸如梯度下降到“调节”全都与减小误差在输出层的目的在网络中的权重。这在下面的图6中示出(现在忽略图中的数学方程)。
假设与所考虑的节点相关联的新权重是w4,w5和w6(反向传播和调整权重之后)。
![]()
图6:多层感知器中的向后传播和权重更新步骤
如果我们现在再次向网络输入相同的例子,那么网络应该比以前更好,因为现在已经调整了权重以最小化预测中的错误。如图7所示,与[0.6,-0.4]相比,输出节点处的误差现在减小到[0.2,-0.2]。这意味着我们的网络已经学会了正确分类我们的第一个培训示例。
![]()
图7:MLP网络现在在同一输入上表现更好
我们重复这个过程与我们的数据集中的所有其他培训示例。然后,我们的网络据说已经学到了这些例子。
如果我们现在想预测一个在中期学习25个小时并有70个学分的学生是否会通过最后一个学期,我们将进行正向传播步骤,找出“通过”和“失败”的输出概率。
我在这里避免了数学方程和概念的解释,例如“渐变下降”,并且相当试图为算法开发直觉。有关反向传播算法的更多数学讨论,请参阅 此链接。
多层感知器的3D可视化
Adam Harley创建了一个多层感知器的 3D可视化,已经在手写数字的MNIST数据库上进行过培训(使用反向传播)。
网络采用784个数字像素值作为手写数字的28×28图像的输入(输入层中有784个节点对应于像素)。网络在第一个隐藏层有300个节点,第二个隐藏层中有100个节点,输出层中有10个节点(对应10位)[15]。
尽管与之前的部分讨论的网络相比,这里描述的网络要大得多(使用更多的隐藏层和节点),正向传播步骤和反向传播步骤中的所有计算都以与所讨论的相同的方式(在每个节点处)完成之前。
图8显示了当输入为数字'5'时的网络。
图8:可视化网络输入'5'
具有较高输出值的节点由较亮的颜色表示。在输入层中,亮点是接收较高数值像素值作为输入的节点。注意在输出层中,唯一的亮点对应于数字5(输出概率为1,高于其他输出概率为0的九个节点)。这表示MLP正确分类了输入数字。我强烈建议玩这个可视化和观察不同层节点之间的连接。
深层神经网络
- 深度学习与普通机器学习有什么区别?
- 神经网络与深层神经网络有什么区别?
- 深层次学习与多层感知器有何不同?
结论
我已经跳过了这篇文章中讨论的一些概念的重要细节,以便于理解。我将推荐通过斯坦福神经网络教程的Part1,Part2,Part3和案例研究,以深入了解多层感知器。
如果您有任何问题或建议,请在下面的意见中通知我们
参考
- 人造神经元模型
- 神经网络第1部分:建立架构(Stanford CNN教程)
- 关于前馈神经网络的维基百科文章
- 维基百科文章关于感知器
- 单层神经网络(感知器)
- 单层感知器
- 加权网络 - 感知器
- 神经网络模型(监督)(scikit学习文档)
- 神经网络中的隐藏层是什么计算?
- 如何选择前馈神经网络中隐藏层和节点的数量?
- 人造神经网络的崩溃介绍
- 为什么BIAS在ANN中是必需的?我们应该为每一层分别设置BIAS吗?
- 基础神经网络教程 - 理论
- 神经网络神秘(视频系列):第1部分,Welch Labs @ MLconf SF
- AW Harley,“An Interactive Node-Link Visualization of Convolutional Neural Networks”,ISVC,page 867-877,2015(link)