基础算法 | 决策树(ID3、C4.5和CART决策树python实现)

决策树(Decision Tree)是一种基于规则的基础而又经典的分类与回归方法，其模型结构呈现树形结构，可认为是一组if-then规则的集合。

决策树主要包含三个步骤：特征选择、决策树构建和决策树剪枝。

典型的决策树有ID3、C4.5和CART(Classification And Regression)，它们的主要区别在于树的结构与构造算法。其中ID3和C4.5只支持分类，而CART支持分类和回归。

1.决策树简介

1.1. ID3决策树

ID3决策树根据信息增益来构建决策树；
对训练集(或子集) D，计算其每个特征的信息增益，并比较大小，选择信息增益最大的特征作为该节点的特征，由该节点的不同取值建立子节点。再对子节点递归以上步骤，构建决策树；直到所有特征的信息增益均小于预设阈值或没有特征为止。

缺点： 信息增益偏向取值较多的特征
$g(D,A)=H(D)-H(D|A)=H(D)-{\sum }_{i=1}^n\frac{|D_i|}{|D|}H(D)=H(D)-(-{\sum }_{i=1}^n\frac{|D_i|}{|D|}{\sum }_{k=1}^k\frac{|D_{ik}|}{|D_i|}lo{g}_2\frac{|D_{ik}|}{|D_i|})$

举个例子，如果以身份证号作为一个属性去划分数据集，则数据集中有多少个人就会有多少个子类别，而每个子类别中只有一个样本，故$lo{g}_2\frac{|D_{ik}|}{|D_i|}=lo{g}_2\frac{1}{1}=0$ 则信息增益$g(D,A)=H(D)$，此时信息增益最大，选择该特征(身份证号)划分数据，然而这种划分毫无意义，但是从信息增益准则来讲，这就是最好的划分属性。

信息增益(information gain)表示得知特征 X 的信息而使得类 Y的信息的不确定性减少的程度。

1.2. C4.5决策树

C4.5决策树根据信息增益比来构建决策树；
C4.5算法与ID3算法只是将ID3中利用信息增益选择特征换成了利用信息增益比选择特征。

1.3. CART决策树

CART决策树根据基尼系数来构建决策树。

算法的终止条件：节点中样本个数小于预定阈值，或者样本中基尼系数小于预定阈值(样本基本属于同一类)，或者没有更多特征。

ID3、C4.5和CART算法对比

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益比	支持	支持	支持
CART	分类、回归	二叉树	基尼系数、均方差	支持	支持	支持

2. 决策树的sklearn实现

决策树的sklearn实现主要是DecisionTreeClassifier函数(分类，回归函数DecisionTreeRegressor)。

class sklearn.tree.DecisionTreeClassifier(
    criterion=’gini’,               # 该函数用于衡量分割的依据。常见的有"gini"用来计算基尼系数和"entropy"用来计算信息增益
    splitter=’best’, 
    max_depth=None,                 # 树的最大深度
    min_samples_split=2,            # 分割内部节点所需的最小样本数
    min_samples_leaf=1,             # 叶节点上所需的最小样本数
    min_weight_fraction_leaf=0.0, 
    max_features=None, 
    random_state=None, 
    max_leaf_nodes=None, 
    min_impurity_decrease=0.0, 
    min_impurity_split=None, 
    class_weight=None, 
    presort=False
)

具体实现如下，完整代码可参考Github

import pickle
import random
import time

import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer, TfidfTransformer
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from tqdm import tqdm


def train_model(train_data, test_data):
    # 打乱样本，以免同类别样本集中
    train_xy = [(cls, d) for cls, data in train_data.items() for d in data]
    random.shuffle(train_xy)
    train_x = [d for _, d in train_xy]
    train_y = [cls for cls, _ in train_xy]
    # train_x, train_y = [], []
    # for cls, data in train_data.items():
    #     train_x += data
    #     train_y += [cls] * len(data)

    t1 = time.time()
    # 将得到的词语转换为词频矩阵
    vectorizer = TfidfVectorizer(min_df=1)
    # 统计每个词语的tf-idf权值
    transformer = TfidfTransformer()
    # 训练tfidf模型
    train_tfidf = transformer.fit_transform(vectorizer.fit_transform(np.array(train_x)))
    # 训练决策树模型
    dt_cls = DecisionTreeClassifier(random_state=0).fit(train_tfidf, train_y)
    t2 = time.time()
    pickle.dump((vectorizer, transformer, dt_cls), open("./model.pickle", "wb"))
    print('train model over. it took {0}ms'.format((t2 - t1)))

    # 预测测试数据
    y_true, y_pred = [], []
    for cls, data in tqdm(test_data.items()):
        for d in data:
            test_tfidf = transformer.transform(vectorizer.transform([d]))
            prediction = dt_cls.predict(test_tfidf)[0]
            y_pred.append(prediction)
            y_true.append(cls)
    # 输出各类别测试测试参数
    classify_report = metrics.classification_report(y_true, y_pred)
    print(classify_report)


if __name__ == '__main__':
    train = pickle.load(open("./train_data.pickle", "rb"))
    test = pickle.load(open("./test_data.pickle", "rb"))
    train_model(train_data=train, test_data=test)

3. 决策树的python实现

ID3和C4.5算法只是特征选择方式不同，其他创建过程一致。完整代码可参考Github

    def create_tree_by_id3_and_c45(self, x, y, feature_list=None):
        """
        创建决策树
        :param x:
        :param y:
        :param feature_list:
        :return:
        """
        # the type is the same, so stop classify
        if len(set(y)) <= 1:
            return y[0]
        # traversal all the features and choose the most frequent feature
        if len(x[0]) == 1:
            return Counter(y).most_common(1)

        feature_list = [i for i in range(len(y))] if not feature_list else feature_list
        if self.decision_tree_type == 'ID3':
            best_feature_idx = self.dataset_split_by_id3(x, y)
        elif self.decision_tree_type == 'C45':
            best_feature_idx = self.dataset_split_by_c45(x, y)
        else:
            raise KeyError
        decision_tree = {best_feature_idx: {}}
        feature_list = feature_list[:best_feature_idx] + feature_list[best_feature_idx + 1:]
        # get the list which attain the whole properties
        best_feature_values = set([sample[best_feature_idx] for sample in x])
        for value in best_feature_values:
            sub_dataset, sub_labels = [], []
            for featVec, label in zip(x, y):
                if featVec[best_feature_idx] == value:
                    sub_dataset.append(list(featVec[:best_feature_idx]) + list(featVec[best_feature_idx + 1:]))
                    sub_labels.append(label)

            decision_tree[best_feature_idx][value] = self.create_tree_by_id3_and_c45(sub_dataset, sub_labels, feature_list)

        return decision_tree

CART根据基尼系数进行特征选择。完整代码可参考Github

    def create_tree_by_cart(self, x, y, feature_list=None):
        """
        输入：训练数据集D，特征集A，阈值ε
        输出：决策树T
        """
        y_lables = np.unique(y)

        # 1、如果数据集D中的所有实例都属于同一类label（Ck），则T为单节点树，并将类label（Ck）作为该结点的类标记，返回T
        if len(set(y_lables)) == 1:
            return y_lables[0]

        # 2、若特征集A=空，则T为单节点，并将数据集D中实例树最大的类label（Ck）作为该节点的类标记，返回T
        if len(x[0]) == 0:
            labelCount = dict(Counter(y_lables))
            return max(labelCount, key=labelCount.get)

        # 3、否则，按CART算法就计算特征集A中各特征对数据集D的Gini，选择Gini指数最小的特征bestFeature（Ag）进行划分
        best_feature_and_idx, _ = self.dataset_split_by_cart(x, y)

        feature_list = [i for i in range(len(x[0]))] if not feature_list else feature_list
        best_feature_idx = feature_list[int(best_feature_and_idx[0])]  # 最佳特征

        decision_tree = {best_feature_idx: {}}  # 构建树，以Gini指数最小的特征bestFeature为子节点
        # feature_list = feature_list[:best_feature_idx] + feature_list[best_feature_idx + 1:]
        feature_list.pop(int(best_feature_and_idx[0]))

        # 使用beatFeature进行划分，划分产生2个节点，成树T，返回T
        y_lables_split = y[list(x[:, int(best_feature_and_idx[0])] == best_feature_and_idx[1])]  # 获取按此划分后y数据列表
        y_lables_grp = Counter(y_lables_split)  # 统计最优划分应该属于哪个i叶子节点“是”、“否”
        y_leaf = y_lables_grp.most_common(1)[0][0]  # 获得划分后出现概率最大的y分类
        decision_tree[best_feature_idx][best_feature_and_idx[1]] = y_leaf  # 设定左枝叶子值

        # 4、删除此最优划分数据x列，使用其他x列数据，递归地调用步1-3，得到子树Ti，返回Ti
        sub_x = np.delete(x, int(best_feature_and_idx[0]), axis=1)  # 删除此最优划分x列，使用剩余的x列进行数据划分
        # 判断右枝类型，划分后的左右枝“是”、“否”是不一定的，所以这里进行判断
        y1 = y_lables[0]  # CART树y只能有2个分类
        y2 = y_lables[1]
        if y_leaf == y1:
            decision_tree[best_feature_idx][y2] = self.create_tree_by_cart(sub_x, y, feature_list)
        elif y_leaf == y2:
            decision_tree[best_feature_idx][y1] = self.create_tree_by_cart(sub_x, y, feature_list)

        return decision_tree

利用《统计学习方法》中P59例子数据

X = [
        ["青年", "否", "否", "一般"],
        ["青年", "否", "否", "好"],
        ["青年", "是", "否", "好"],
        ["青年", "是", "是", "一般"],
        ["青年", "否", "否", "一般"],
        ["中年", "否", "否", "一般"],
        ["中年", "否", "否", "好"],
        ["中年", "是", "是", "好"],
        ["中年", "否", "是", "非常好"],
        ["中年", "否", "是", "非常好"],
        ["老年", "否", "是", "非常好"],
        ["老年", "否", "是", "好"],
        ["老年", "是", "否", "好"],
        ["老年", "是", "否", "非常好"],
        ["老年", "否", "否", "一般"]
    ]
    Y = ["否", "否", "是", "是", "否", "否", "否", "是", "是", "是", "是", "是", "是", "是", "否"]

生成决策树，可视化代码可参考Github


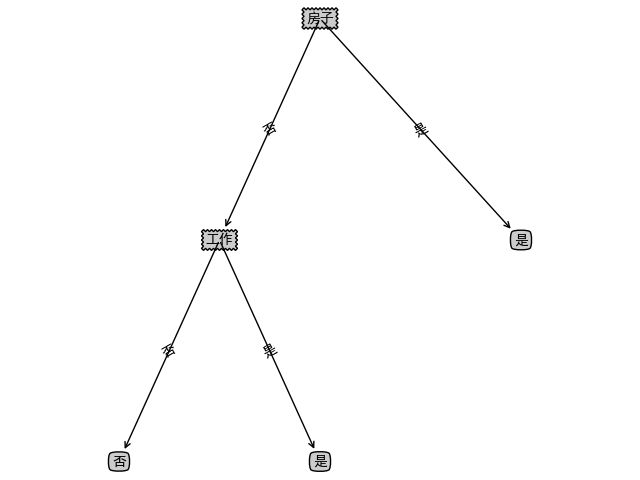
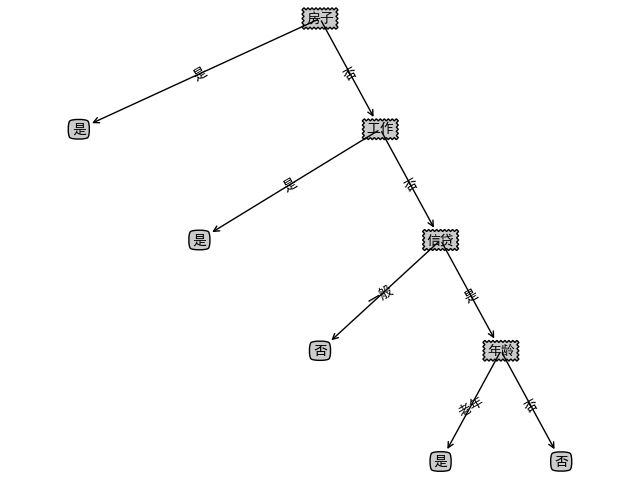
本文中所有代码已上传Github。

参考

1. 机器学习基础之一文读懂决策树
   
2. 机器学习之-常见决策树算法(ID3、C4.5、CART)
   
3. Python实现决策树2(CART分类树及CART回归树)