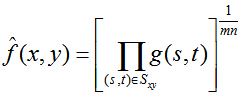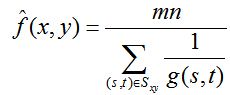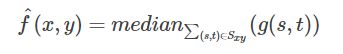均值滤波器

一、算术均值滤波器

1.1 原理：简单使用定义区域中的像素得出算术均值

1.2 公式

1.3 代码

#include 
#include "pch.h"
#include 
using namespace std;
using namespace cv;

/* Salt&pepper noise 椒盐噪声 */
void noise(Mat &image, float ratio) {
    int n = image.rows * image.cols * ratio;
    for (int k = 0; k < n; k++) {
        int i = rand() % image.rows;
        int j = rand() % image.cols;
        int type = rand() % 2;

        if (type == 1) {
            image.at(i, j)[0] = 255;
            image.at(i, j)[1] = 255;
            image.at(i, j)[2] = 255;
        }
        else
        {
            image.at(i, j)[0] = 0;
            image.at(i, j)[1] = 0;
            image.at(i, j)[2] = 0;
        }
    }
}

/* Arithmetic mean filter 算术均值滤波器 */
double filterArithmeticMean(Mat src) {
    double sum = 0;
    for (int i = 0; i < src.rows; i++) {
        uchar* data = src.ptr(i);
        for (int j = 0; j < src.cols; j++) {
            sum += double(data[j]);
        }
    }
    return sum / double(src.cols*src.rows);
}

/* Filter 滤波器 */
Mat filter(Mat image, Size size) {
    Mat result;
    image.copyTo(result);
    Mat channel[3];
    split(image, channel);
    int l = (size.height - 1) / 2;
    int w = (size.width - 1) / 2;
    for (int i = l; i < result.rows - l; i++) {
        for (int j = w; j < result.cols - w; j++) {
            for (int ii = 0; ii < 3; ii++) {
                result.at(i, j)[ii] = saturate_cast(filterArithmeticMean(channel[ii](Rect(j - w, i - l, size.width, size.height))));
            }
        }
    }
    return result;
}

int main()
{
    Mat img = imread("head.jpg");

    // 噪声处理
    noise(img, 0.1);
    imshow("Noised", img);

    // 滤波处理
    Mat result = filter(img, Size(3, 3));
    imshow("Denoised", result);

    waitKey();
    return 0;
}

1.4 效果

二、几何均值滤波器

2.1 原理：每个复原的像素由子图像窗口中像素数的乘积的1/mn次幂给出

2.2 公式

2.3 代码

#include 
#include "pch.h"
#include 
using namespace std;
using namespace cv;

/* Salt&pepper noise 椒盐噪声 */
void noise(Mat &image, float ratio) {
    int n = image.rows * image.cols * ratio;
    for (int k = 0; k < n; k++) {
        int i = rand() % image.rows;
        int j = rand() % image.cols;
        int type = rand() % 2;

        if (type == 1) {
            image.at(i, j)[0] = 255;
            image.at(i, j)[1] = 255;
            image.at(i, j)[2] = 255;
        }
        else
        {
            image.at(i, j)[0] = 0;
            image.at(i, j)[1] = 0;
            image.at(i, j)[2] = 0;
        }
    }
}

/* Geometric mean filtering 几何均值滤波器 */
double filterGeometricMean(Mat src) {
    double geo = 1;
    for (int i = 0; i < src.rows; i++) {
        uchar* data = src.ptr(i);
        for (int j = 0; j < src.cols; j++) {
            if (data[j] != 0)
                geo *= data[j];
        }
    }
    double power = 1.0 / double(src.rows*src.cols);
    return pow(geo, power);
}

/* Filter 滤波器 */
Mat filter(Mat image, Size size) {
    Mat result;
    image.copyTo(result);
    Mat channel[3];
    split(image, channel);
    int l = (size.height - 1) / 2;
    int w = (size.width - 1) / 2;
    for (int i = l; i < result.rows - l; i++) {
        for (int j = w; j < result.cols - w; j++) {
            for (int ii = 0; ii < 3; ii++) {
                result.at(i, j)[ii] = saturate_cast(filterGeometricMean(channel[ii](Rect(j - w, i - l, size.width, size.height))));
            }
        }
    }
    return result;
}

int main()
{
    Mat img = imread("input.jpg");

    // 噪声处理
    noise(img, 0.01);
    imshow("Noised", img);

    // 滤波处理
    Mat result = filter(img, Size(3, 3));
    imshow("Denoised", result);

    waitKey();
    return 0;
}

2.4 效果

三、谐波均值滤波器

3.1 原理：谐波均值滤波器对于盐粒噪声效果较好，但不适用于胡椒噪声

3.2 公式

3.3 代码

#include 
#include "pch.h"
#include 
using namespace std;
using namespace cv;

/* Salt&pepper noise 椒盐噪声 */
void noise(Mat &image, float ratio) {
    int n = image.rows * image.cols * ratio;
    for (int k = 0; k < n; k++) {
        int i = rand() % image.rows;
        int j = rand() % image.cols;
        int type = rand() % 2;

        if (type == 1) {
            image.at(i, j)[0] = 255;
            image.at(i, j)[1] = 255;
            image.at(i, j)[2] = 255;
        }
        else
        {
            image.at(i, j)[0] = 0;
            image.at(i, j)[1] = 0;
            image.at(i, j)[2] = 0;
        }
    }
}

/* Harmonic mean filter 谐波均值滤波器 */
double filterHarmonicMean(Mat src) {
    double harmonic = 0;
    for (int i = 0; i < src.rows; i++) {
        uchar* data = src.ptr(i);
        for (int j = 0; j < src.cols; j++) {
            if (data[j] != 0)
                harmonic += 1 / (double)data[j];
        }
    }
    return (src.rows*src.cols) / harmonic;
}

/* Filter 滤波器 */
Mat filter(Mat image, Size size) {
    Mat result;
    image.copyTo(result);
    Mat channel[3];
    split(image, channel);
    int l = (size.height - 1) / 2;
    int w = (size.width - 1) / 2;
    for (int i = l; i < result.rows - l; i++) {
        for (int j = w; j < result.cols - w; j++) {
            for (int ii = 0; ii < 3; ii++) {
                result.at(i, j)[ii] = saturate_cast(filterHarmonicMean(channel[ii](Rect(j - w, i - l, size.width, size.height))));
            }
        }
    }
    return result;
}

int main()
{
    Mat img = imread("input.jpg");

    // 噪声处理
    noise(img, 0.01);
    imshow("Noised", img);

    // 滤波处理
    Mat result = filter(img, Size(3, 3));
    imshow("Denoised", result);

    waitKey();
    return 0;
}

3.4 效果

四、中值滤波器

4.1 原理：使用一个像素领域中的灰度级的中值来替代该像素的值

4.2 公式

4.3 代码

#include 
#include "pch.h"
#include 
using namespace std;
using namespace cv;

/* Salt&pepper noise 椒盐噪声 */
void noise(Mat &image, float ratio) {
    int n = image.rows * image.cols * ratio;
    for (int k = 0; k < n; k++) {
        int i = rand() % image.rows;
        int j = rand() % image.cols;
        int type = rand() % 2;

        if (type == 1) {
            image.at(i, j)[0] = 255;
            image.at(i, j)[1] = 255;
            image.at(i, j)[2] = 255;
        }
        else
        {
            image.at(i, j)[0] = 0;
            image.at(i, j)[1] = 0;
            image.at(i, j)[2] = 0;
        }
    }
}

/* Bubble sort 冒泡排序 */
void bubbleSort(float* pData, int count) {
    float tData;
    for (int i = 1; i < count; i++) {
        for (int j = count - 1; j > -i; j--) {
            if (pData[j] < pData[j - 1]) {
                tData = pData[j - 1];
                pData[j - 1] = pData[j];
                pData[j] = tData;
            }
        }
    }
}



/* Median filter 中值滤波器 */
double filterMedian(Mat src) {
    int index = 0;
    int length = src.rows * src.cols;
    float* bubble = new float[length];
    for (int i = 0; i < src.rows; i++) {
        uchar* data = src.ptr(i);
        for (int j = 0; j < src.cols; j++) {
            bubble[index] = data[j];
            index++;
        }
    }
    bubbleSort(bubble, length);
    double median = bubble[length / 2];
    return median;
}

/* Filter 滤波器 */
Mat filter(Mat image, Size size) {
    Mat result;
    image.copyTo(result);
    Mat channel[3];
    split(image, channel);
    int l = (size.height - 1) / 2;
    int w = (size.width - 1) / 2;
    for (int i = l; i < result.rows - l; i++) {
        for (int j = w; j < result.cols - w; j++) {
            for (int ii = 0; ii < 3; ii++) {
                result.at(i, j)[ii] = saturate_cast(filterMedian(channel[ii](Rect(j - w, i - l, size.width, size.height))));
            }
        }
    }
    return result;
}

int main()
{
    Mat img = imread("input.jpg");

    // 噪声处理
    noise(img, 0.01);
    imshow("Noised", img);

    // 滤波处理
    Mat result = filter(img, Size(3, 3));
    imshow("Denoised", result);

    waitKey();
    return 0;
}

4.4 效果

参考链接：https://blog.csdn.net/wzmsltw/article/details/52927787