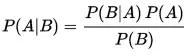贝叶斯公式的应用
观点应该跟着事实不断修订,坚定不移不对,听风就是雨也不对 ---- 科学的修正(correction),就是贝叶斯方法。
P(A|B)指的是条件概率,即在B已经发生的情况下,A发生的概率
平时我们对存在外星人(记作事件A)这一观点的相信的概率可以用P(A)来表示,一般而言咱都不怎么相信外星人存在的,P(A) ~= 0,可是突然有一天一个正儿八经的专家说证明确实有外星人存在(记为事件B),那此时,我们相信外星人存在的概率已经不是P(A)了,而是P(A|B),而这个值可能就要比0大不少了。要是某一天,大半个地球的人都说看到了外星人(记为C),那我们此时相信外星人存在的概率P(A|C)可能就要提高到1,也就是几乎确定就是有外星人存在。
-
Accumulation of evidence --> The probability is increasing
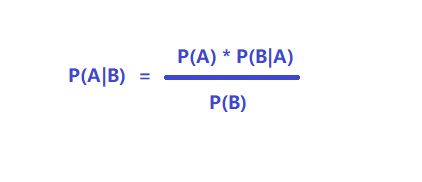
贝叶斯公式:
其中 P(A) 是我们原来对一件事的原有的判断,叫做先验概率
P(A|B) 就代表了我们在得到一些证据B之后对原来事物的概率,叫做后验概率
有个简单的理解方法:我们把等式右边P(B|A) / P(B)看作一个整体,称之为似然比(可以简单理解成证据的有效程度), 那么整个公式便可以简单理解成P(你后来的观点)= 似然比 * P(你一开始的观点)。当有新的证据出现之后,别忙着不变,也别忙着立马推翻自己的态度,看看证据的有效性如何,如果真的有效,那就多调整一点自己的态度,如果证据的力度不大,那就少调整一点。卡尔·萨根说过一句话:“超乎寻常的论断需要超乎寻常的证据”,在贝叶斯看来这句话的意思不过是,要想从根本上说服我,你必须拿出唬得住我的东西来。
例子 一
在狼来了的故事中,我们用
A: 表示小孩可信 B: 表示小孩说谎
Assumption:
P(A)=0.8 (P(~A)=0.2)
P(A|B),即小孩说了一次慌之后的可信程度
P(B): (在任何条件下)小孩子说谎的概率,可以拆分为P(A)*P(B|A)和P(~A)*P(B|~A),
P(B|A)和P(B|~A)分别表示在我们相信他时他说谎的概率和我们不相信他时他说谎的概率,分为设之为0.1和0.5
有一天小孩是说狼来了,80%的可能性狼来了,我们想吃狼肉,于是我们第一次上山打狼,发现狼没有来,即小孩子说了谎。此时P(A|B) = P(A) * P(B|A) / P(B) = 0.8*0.1 / (0.8*0.1 + 0.2*0.5) = 0.444,表明我们上一次当之后对这个小孩的可信程度从0.8下降到了0.444。在此基础之上,有一天小孩又说狼来了,有44.4%的可能性狼来了,本来不想去的,但是上次没吃到狼肉心里痒痒,于是我们又上山打狼,结果小孩又对我们撒了一次谎,狼没有来。我们对他的可信程度P(A|B) =0.444*0.1 /(0.444*0.1 +0.556*0.5) = 0.138,我们上了这小孩两次当,对小孩的可信程度由原来的0.8下降到了0.138
例子 二
很多时候,并不是贝叶斯公式太难,只不过是我们不知道贝叶斯公式使用的时机。贝叶斯的应用领域极其广泛,语音识别、垃圾邮件过滤、油井钻探、FDA批准新药、Xbox给你的游戏水平打分……各种你想到和想不到的应用,都在使用贝叶斯方法。我们的市井生活中什么时候该用贝叶斯公式呢?很简单:只要还没得到最终结果,就可以请贝叶斯爸爸出场。
你和两位同学在操场上看到了一位身材火辣的性感女神,决定写纸条抽签选一人去要联系方式。每人抽到一个签,中彩概率都是1/3,很公平。你抽到了一张签,觉得不会是自己,刚准备看,突然一位同学摊出了自己的纸条,哈哈大笑说:“看不是我。” 此时,天真的你觉得那有啥,反正大家中彩的概率依旧还是1/3,而且我运气好,不可能是我。
记你中彩为事件A,P(A)=1/3
那个已经摊出纸条的同学没有中彩为事件B,P(B)=2/3
你现在中彩的概率P(A|B) = P(A) * P(B|A) / P(B) = (1/3) * 1 /(2/3)= 1/2 , 所以你的概率上升了。
例子 三
我们可以用贝叶斯定理推算一下为什么大多数人会认为东北人酒量大。已知:
P(A)=遇见酒量大的人的概率。
P(B) = 遇见东北人的概率。
P(B|A) = 遇见酒量大的人是东北人的概率
那么,遇见东北人的酒量大的概率P(A|B) = P(A)*P(B|A)/P(B) =遇见酒量大的人的概率X遇见酒量大的人是东北人的概率/遇见东北人的概率。
从这个公式P(A|B) = P(A)*P(B|A)/P(B)中可以看出,我们还可以学到如何降低对东北人酒量大的偏见:
1.减少遇见酒量大的人的概率,遇见酒量大的人是东北人的概率。这两点很难控制,碰到的人酒量怎么样我们无法控制,碰到的这个酒量大的人是哪里人我们也无法控制。
2.增加遇见东北人的概率。这点我们可以控制,比如去东北,或去东北人多的地方。了解了更多的东北人后,P(A|B)的概率下降,减少我们对东北人的酒量大的偏见。
其实,对于所有的偏见,不管地域偏见,还是阶层偏见,只要更多的去了解被偏见的对象,偏见都会减少。
例子 四
贝叶斯定理还经常被应用在机器学习中,比如对垃圾邮件分类。假如,现在我们有10万邮件,每个邮件都已经被标记好了是否是垃圾邮件。通过这些数据我们很容易计算出:
P(A)=垃圾邮件的概率,垃圾邮件/所有的邮件。
P(B) = 邮件中出现词M的概率,出现词M的邮件/所有的邮件。
P(B|A) = 垃圾邮件中出现词M概率,垃圾邮件中含有词M的邮件数量/所有的垃圾邮件。
那么,出现词M的邮件是垃圾邮件的概率P(A|B) = P(A)*P(B|A)/P(B) =邮件中出现词M的概率X垃圾邮件中出现词M概率/是垃圾邮件的概率。
对垃圾邮件学习的过程就是计算P(A|B)的过程。一般会有多个词或多个词的组合尝试,直到找到概率大于预期概率(比如。0.8,0.9等)的词M或一组词M1,M2等。然后就可以用得到的词计算,判断新的邮件是否是垃圾邮件。
例子 五
贝叶斯(Bayes)公式是解决由观察到的现象/测量的数据去推断现象/数据后面的规律的发生的概率的问题。那么如果将上面公式中的A换成“规律”,B换成“现象”,这个公式就一目了然,能很容易理解和运用了。
理解和运用贝叶斯公式的关键是:理清问题中的规律和现象!
思考题:
-
垃圾邮件检测中,什么是规律,什么是现象?
-
拼写错误纠正中,什么是规律,什么是现象?
例子 六
我们选取“祥源文化(股票代码:600576)来进行分析
作者发布这篇文章的时间是星期天凌晨(2018年1月14日),来判断周一(也就是2018年1月15日)。在周一(2018年1月15日)上证指数上涨的情况下,祥源文化这支股票上涨的概率。
表示为:P(祥源文化上涨|上证指数上涨)
我们先收集一下近半年内,祥源文化和上证指数在每周一的情况:
祥源文化
| 序号 |
时间 |
星期 |
是否上涨 |
| 1 |
2017/6/5 |
星期一 |
1 |
| 2 |
2017/6/12 |
星期一 |
0 |
| 3 |
2017/6/19 |
星期一 |
1 |
| 4 |
2017/6/26 |
星期一 |
1 |
| 5 |
2017/7/3 |
星期一 |
1 |
| 6 |
2017/7/10 |
星期一 |
0 |
| 7 |
2017/7/17 |
星期一 |
0 |
| 8 |
2017/7/24 |
星期一 |
0 |
| 9 |
2017/7/31 |
星期一 |
0 |
| 10 |
2017/8/7 |
星期一 |
1 |
| 11 |
2017/8/14 |
星期一 |
1 |
| 12 |
2017/8/21 |
星期一 |
1 |
| 13 |
2017/8/28 |
星期一 |
1 |
| 14 |
2017/9/4 |
星期一 |
0 |
| 15 |
2017/9/11 |
星期一 |
1 |
| 16 |
2017/9/18 |
星期一 |
1 |
| 17 |
2017/9/25 |
星期一 |
1 |
| 18 |
2017/10/9 |
星期一 |
1 |
| 19 |
2017/10/16 |
星期一 |
0 |
| 20 |
2017/10/23 |
星期一 |
0 |
| 21 |
2017/10/30 |
星期一 |
0 |
| 22 |
2017/11/6 |
星期一 |
1 |
| 23 |
2017/11/13 |
星期一 |
0 |
| 24 |
2017/11/20 |
星期一 |
0 |
| 25 |
2017/11/27 |
星期一 |
0 |
| 26 |
2017/12/4 |
星期一 |
0 |
| 27 |
2017/12/11 |
星期一 |
1 |
| 28 |
2017/12/18 |
星期一 |
0 |
| 29 |
2017/12/25 |
星期一 |
0 |
| 30 |
2018/1/8 |
星期一 |
0 |
| 14 |
上证指数
| 序号 |
时间 |
星期 |
是否上涨 |
| 1 |
2017/6/5 |
星期一 |
0 |
| 2 |
2017/6/12 |
星期一 |
0 |
| 3 |
2017/6/19 |
星期一 |
1 |
| 4 |
2017/6/26 |
星期一 |
1 |
| 5 |
2017/7/3 |
星期一 |
1 |
| 6 |
2017/7/10 |
星期一 |
0 |
| 7 |
2017/7/17 |
星期一 |
0 |
| 8 |
2017/7/24 |
星期一 |
1 |
| 9 |
2017/7/31 |
星期一 |
1 |
| 10 |
2017/8/7 |
星期一 |
1 |
| 11 |
2017/8/14 |
星期一 |
1 |
| 12 |
2017/8/21 |
星期一 |
1 |
| 13 |
2017/8/28 |
星期一 |
1 |
| 14 |
2017/9/4 |
星期一 |
1 |
| 15 |
2017/9/11 |
星期一 |
1 |
| 16 |
2017/9/18 |
星期一 |
1 |
| 17 |
2017/9/25 |
星期一 |
0 |
| 18 |
2017/10/9 |
星期一 |
1 |
| 19 |
2017/10/16 |
星期一 |
0 |
| 20 |
2017/10/23 |
星期一 |
1 |
| 21 |
2017/10/30 |
星期一 |
0 |
| 22 |
2017/11/6 |
星期一 |
1 |
| 23 |
2017/11/13 |
星期一 |
1 |
| 24 |
2017/11/20 |
星期一 |
1 |
| 25 |
2017/11/27 |
星期一 |
0 |
| 26 |
2017/12/4 |
星期一 |
0 |
| 27 |
2017/12/11 |
星期一 |
1 |
| 28 |
2017/12/18 |
星期一 |
1 |
| 29 |
2017/12/25 |
星期一 |
0 |
| 30 |
2018/1/8 |
星期一 |
1 |
| 20 |
由两个表的数据,我们可以得出以下数据:
| 事件 |
概率 |
| 祥源文化上涨 (A) |
P(A) =14/30 即:7/15 |
| 上证指数上涨 (B) |
P(B) =20/30 即: 2/3 |
而P (上证指数上涨|祥源文化上涨) ,我们根据历史数据,预估为0.9:即 P(B|A) =0.9
所以,我们得出:
P(A|B)= 0.9*(7/15)/(2/3)= 0.63
所以结论就是,在周一(2018年1月15日)上证指数上涨的情况下,祥源文化这支股票上涨的概率是0.63。也就是说,周一(2018年1月15日)只要上证指数是上涨的,祥源文化大可能也是会上涨的。
大家发现没有,概率最大的作用是将商业和日常生活中遇到的各种不确定性量化了。
例子 七
假如你是一个女生, 你在你的老公书包里发现了一个别的女人的内裤那么他出轨的概率是多少。
把这个问题分解为几步考虑:
1 你老公在没有任何概率情况下出轨的概率是多少? 如果他是个天生老实巴交的程序员或者风流倜傥的CEO, 那么显然不该一视同仁
2 如果你老公出轨了, 那么他有一条内裤的概率是多少, 如果他没出轨, 出现这个情况概率有多少? 想想一般人即使出轨也不会犯那么傻的错误, 会不会有没出轨而出现内裤的状况? 有没有可能是某个暗恋你老公的人的陷害?
3 根据1 和2求解最终问题,这才是拥有大学数学能力的你该做的分析。
在这里1其实就是先验概率P(A),而2是条件概率P(B|A), 最终得到3后验概率P(A|B) 这三种即是贝叶斯统计的三要素
基于条件概率的贝叶斯定律数学方程极为简单:
A即出轨, B是内裤出现, 你得到1,2,就可以根据公式算出根据根据内裤出现判断出轨的概率。
先验概率在贝叶斯统计中具有重要意义,首先先验概率即我们在取得证据之前所指定的概率P(A), 这个值通常是根据我们之前的常识,带有一定的主观色彩。 就像刚刚说的出轨的问题, 你的先验概率代表了你对你男人的信心。
有一个非常有趣的现象是如果我们的先验概率审定为1或0(即肯定或否定某件事发生),那么无论我们如何增加证据你也依然得到同样的条件概率(此时P(A)=0 或 1 ,P(A|B)= 0或1) 这告诉我们的第一个经验就是不要过早的下论断
贝叶斯分析中的三要素在不同的问题中通常侧重点不同,很多时候我们都是在忽略先验概率的作用,比如描述一个人很书呆子气让你判断他是大学老师还是销售员的经典案例(要看先验大学老师还是销售员哪个多啊)
例子 八 贝叶斯分析看辛普森案
比如著名的辛普森案, 为了证明辛普森有杀妻之罪,检方说辛普森之前家暴,而辩护律师说,美国有400万女性被丈夫或男友打过,而其中只有1432人被杀,概率是2800分之一
********************* 70%的凶杀案都发生在熟人之间 (如男女关系,朋友关系) *********************
这其实就是误用了后验概率, 这里的条件是被杀而且有家暴,而要推测的事件是凶手是男友(事实上概率高达90%),这才是贝叶斯分析的正当用法, 而辩护律师却是在混淆条件与要验证的假设 ---- (弄反条件与假设)
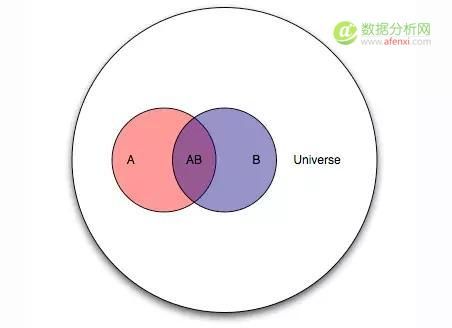
理解贝叶斯分析最好的方法即图像法, 这里的A的面积即先验, 后验是阴影占蓝圈的百分比。
贝叶斯分析可以瞬间理解一些常用的理论, 如幸存者偏差,你发现一些没读过书的人很有钱,事实上是你发现就已经是幸存者了(对应上图中小红圈), 而死了的人(红圈外的大部分面积)你都没见到啊。
还有阴谋论, 阴谋论的特点是条件很多很复杂, 但是条件一旦成立,结论几乎成立,你一旦考虑了先验,这些条件成立本身即很困难, 阴谋论不攻自克。
此处贝叶斯分析的框架也在教我们如何处理特例与一般常识的规律。
如果你太注重特例(即完全不看先验概率) 很有可能会误把噪声看做信号, 而奋不顾身的跳下去。
如果恪守先验概率, 就成为无视变化而墨守成规的人。其实会贝叶斯的人生存率会更高, 因为他们会重视特例, 但也不忘记书本的经验,根据贝叶斯公式小心调整信心,甚至会主动设计实验根据信号判断假设,这就是我们下一步要讲的。
朴素贝叶斯,核心在于假设证据互相独立。由此我们得到下列乘法公式(feature对应x)
用数学语言白表征这个问题, X特征向量,h把X映射成不同的分类, 我们要求得是P(y|x) 正确率最大的假设(y)
Reference
1 贝叶斯公式的现实应用
2 贝叶斯定理的实际应用
3 真的理解贝叶斯公式吗?
4 金融工程基础实战之贝叶斯股票投资决策
5 https://blog.csdn.net/sinat_26230689/article/details/52664078