EfficientNet论文阅读笔记
目录
论文信息
摘要
问题制定
模型缩放
高效地网络架构
实验结果
论文信息
链接:http://arxiv.org/pdf/1905.11946v2.pdf
发表时间:2019
来源:google
作者:Mingxing Tan
摘要
卷积神经网络(ConvNets)通常是在固定的资源预算下开发的,如果有更多的资源,则可以按比例放大以获得更高的准确性。在本文中,系统地研究了模型缩放并确定仔细地平衡网络深度,宽度和分辨率可以带来更好的性能。基于这一观察,提出了一种新的缩放方法,该方法使用简单但高效的复合系数均匀地缩放深度/宽度/分辨率的所有维度。证明了这种方法在扩展MobileNets和ResNet方面的有效性。
问题制定
卷积层可以定义为函数 ![]() ,其中
,其中![]() 是卷积运算符,
是卷积运算符,![]() 表示输出张量,
表示输出张量,![]() 表示输入张量,张量形状为
表示输入张量,张量形状为![]() 表示输入张量的形状,其中
表示输入张量的形状,其中![]() 是feature map的尺寸,
是feature map的尺寸,![]() 是通道维度。卷积可以用一系列组成层表示:
是通道维度。卷积可以用一系列组成层表示:![]() 。实践中,ConvNet层经常被划分为多个stages,并且每个stage的所有层共享相同的结构:举个例子,ResNet有5个stages,每个stage的所有层有相同的卷积类型(除了第一层有一个下采样),因此,我们可以将ConvNet定义为:
。实践中,ConvNet层经常被划分为多个stages,并且每个stage的所有层共享相同的结构:举个例子,ResNet有5个stages,每个stage的所有层有相同的卷积类型(除了第一层有一个下采样),因此,我们可以将ConvNet定义为:
![]() (1)
(1)
其中N是分类网络,X表示输入,![]() 表示
表示![]() 在阶段i中重复
在阶段i中重复![]() 次,总共有s个stage,
次,总共有s个stage,![]() 表示层i的输入张量X的形状。为了进一步减小设计空间,我们限制所有层必须以恒定比率均匀缩放。我们的目标是最大化任何给定资源约束的模型精度,这可以表示为优化问题:
表示层i的输入张量X的形状。为了进一步减小设计空间,我们限制所有层必须以恒定比率均匀缩放。我们的目标是最大化任何给定资源约束的模型精度,这可以表示为优化问题:
模型缩放
我们假定卷积层的输入特征图大小是:
![]()
输出特征图大小是:
![]()
对于卷积:
![]()
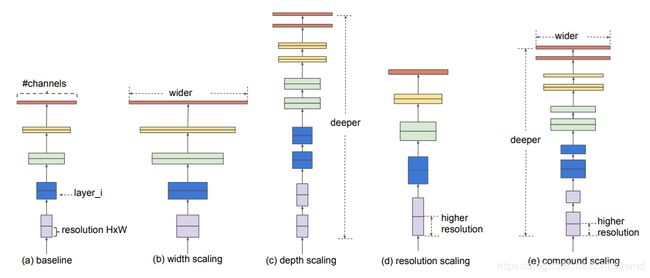
上图中(a)baseline的计算量是:
![]()
-
网络深度(d)缩放
网络深度指卷积层的层数,如上图(c)所示。这里假设深度缩放![]() 倍,则计算量是:
倍,则计算量是:
![]()
缩放网络深度是许多ConvNets最常用的方式。直觉是更深层次的ConvNet可以捕获更丰富,更复杂的特征,并且可以很好地概括新任务。然而,由于消失的梯度问题,更深的网络也更难以训练。虽然跳线连接和batch normalization等几种技术可以缓解训练问题,但非常深的网络的准确度增加会减少。
- 网络宽度(w)缩放
在卷积运算中,网络宽度指网络输入输出的通道数,如上图(b)所示。这里假设宽度缩放![]() 倍,则计算量是:
倍,则计算量是:
![]()
计算量变为原来的![]() 倍,缩放网络宽度通常用于小尺寸模型,更广泛的网络往往能够捕获更多细粒度的特征并且更容易训练。然而,极宽但浅的网络往往在捕获更高级别的特征方面存在困难。而且当网络变得更宽,w越大时,准确度就会快速饱和。
倍,缩放网络宽度通常用于小尺寸模型,更广泛的网络往往能够捕获更多细粒度的特征并且更容易训练。然而,极宽但浅的网络往往在捕获更高级别的特征方面存在困难。而且当网络变得更宽,w越大时,准确度就会快速饱和。
- 网络分辨率(r)缩放
分辨率缩放指改变卷积层输入输出的图形分辨率。这里假设分辨率缩放![]() 倍,则计算量是:
倍,则计算量是:
![]()
计算量变为原来的![]() 倍,使用更高分辨率的输入图像,ConvNets可以捕获更多细粒度的图案。
倍,使用更高分辨率的输入图像,ConvNets可以捕获更多细粒度的图案。
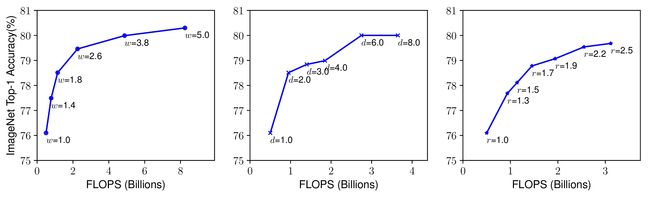
扩展具有不同网络宽度(w),深度(d)和分辨率(r)的基线模型。具有更大宽度,深度或分辨率的更大网络倾向于实现更高的准确度,但是在达到80%之后准确度增益快速饱和,证明了单维缩放的限制。深度或分辨率的任何尺寸都可以提高精度,但对于较大的模型,精度增益会降低。
不同的缩放尺寸不是独立的。直观地,对于更高分辨率的图像,我们应该增加网络深度,使得更大的感受野可以帮助捕获包括更大图像中的更多像素的类似特征。相应地,我们还应该在分辨率更高时增加网络宽度,以便在高分辨率图像中捕获具有更多像素的更多细粒度图案。这些直觉表明我们需要协调和平衡不同的缩放尺寸,而不是传统的单维缩放。
- 复合缩放
为了追去更好的精度和效率,在缩放时平衡网络所有维度至关重要。提出了一种新的复合缩放方法,它使用复合系数![]() 以原则方式统一缩放网络宽度,深度和分辨率:
以原则方式统一缩放网络宽度,深度和分辨率:
(3)
其中![]() 是可以通过小网格搜索确定的常量。直观地说,
是可以通过小网格搜索确定的常量。直观地说,![]() 是一个用户指定的系数,它控制有多少资源可用于模型缩放,而
是一个用户指定的系数,它控制有多少资源可用于模型缩放,而![]() 则分别指定如何将这些额外资源分配给网络宽度,深度和分辨率。值得注意的是,常规卷积运算的FLOPS与d,
则分别指定如何将这些额外资源分配给网络宽度,深度和分辨率。值得注意的是,常规卷积运算的FLOPS与d,![]() ,
,![]() 成正比,即双倍网络深度将使FLOPS加倍,但网络宽度或分辨率加倍会使FLOPS增加四倍。由于卷积运算通常主导ConvNets中的计算成本,因此使用上面等式对ConvNet进行缩放将使总FLOPS增加。在本文中,我们约束
成正比,即双倍网络深度将使FLOPS加倍,但网络宽度或分辨率加倍会使FLOPS增加四倍。由于卷积运算通常主导ConvNets中的计算成本,因此使用上面等式对ConvNet进行缩放将使总FLOPS增加。在本文中,我们约束![]() ,这样对于任何新的
,这样对于任何新的![]() ,总FLOPS将大约增加
,总FLOPS将大约增加![]() 。
。
高效地网络架构
由于模型的缩放不会改变基线网络中的层运算,因此具有良好的基线网络也很关键。为了更好地展示我们缩放方法的有效性,我们还开发了一种新的移动尺寸基线,称为EfficientNet。受到MnasNet的启发,我们通过利用多目标的神经网络结构搜索来同时优化精度和FLOPS,我们的搜索空间和MnasNet相同,并使用![]() 作为优化目标 ,其中ACC(m)和FLOPS(m)分别是模型m的精度和计算量,T是目标计算量,w=−0.07是一个超参数用来权衡精度和FLOPS。不像MnasNet中的优化目标,这里优化的是FLOPS而不是延迟,因为我们没有说是要在特定的硬件平台上做加速。我们的搜索方法得到了一个高效的网络,我们称之为EfficientNet-B0,因为我们使用的搜索空间和MnasNet相似,所以得到的网络结构也很相似,不过我们的EfficientNet-B0稍微大了点,因为我们的FLOPS预算也比MnasNet中大(400M)。下表展示了EfficientNet-B0的结构,它的主要构建块就是移动倒置瓶颈MBConv。
作为优化目标 ,其中ACC(m)和FLOPS(m)分别是模型m的精度和计算量,T是目标计算量,w=−0.07是一个超参数用来权衡精度和FLOPS。不像MnasNet中的优化目标,这里优化的是FLOPS而不是延迟,因为我们没有说是要在特定的硬件平台上做加速。我们的搜索方法得到了一个高效的网络,我们称之为EfficientNet-B0,因为我们使用的搜索空间和MnasNet相似,所以得到的网络结构也很相似,不过我们的EfficientNet-B0稍微大了点,因为我们的FLOPS预算也比MnasNet中大(400M)。下表展示了EfficientNet-B0的结构,它的主要构建块就是移动倒置瓶颈MBConv。
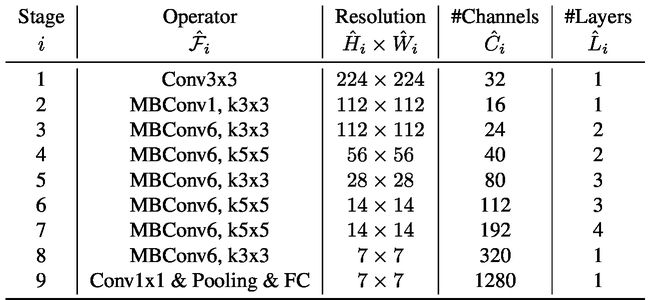
上表展示的EfficientNet-B0是基线网络, 每行描述了具有![]() 层的阶段i,输入分辨率为
层的阶段i,输入分辨率为![]()
![]()
![]() ,输出通道为
,输出通道为![]() 。然后以EfficientNet-B0为baseline模型,我们将我们的复合缩放方法应用到它上面,分为两步:
。然后以EfficientNet-B0为baseline模型,我们将我们的复合缩放方法应用到它上面,分为两步:
(1)我们首先固定![]() ,假设有相比于原来多了2倍的资源,我们基于等式(2)和(3)先做了一个小范围的搜索,最后发现对于EfficientNet-B0来说最后的值为
,假设有相比于原来多了2倍的资源,我们基于等式(2)和(3)先做了一个小范围的搜索,最后发现对于EfficientNet-B0来说最后的值为![]() ,在
,在![]() 的约束下;
的约束下;
(2)然后我们将![]() 作为常数并使用公式(3)使用不同的
作为常数并使用公式(3)使用不同的![]() 扩展基线网络,以获得EfficientNet-B1至B7。
扩展基线网络,以获得EfficientNet-B1至B7。
实验结果
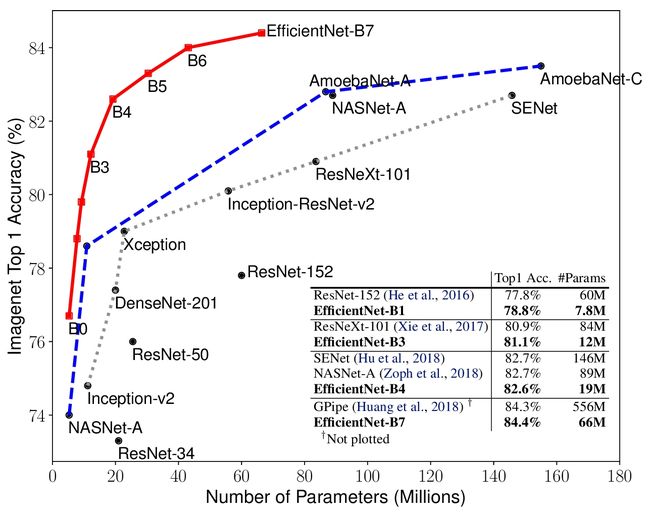
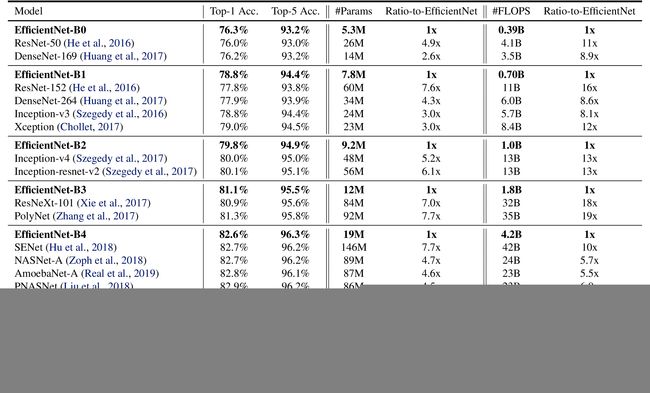
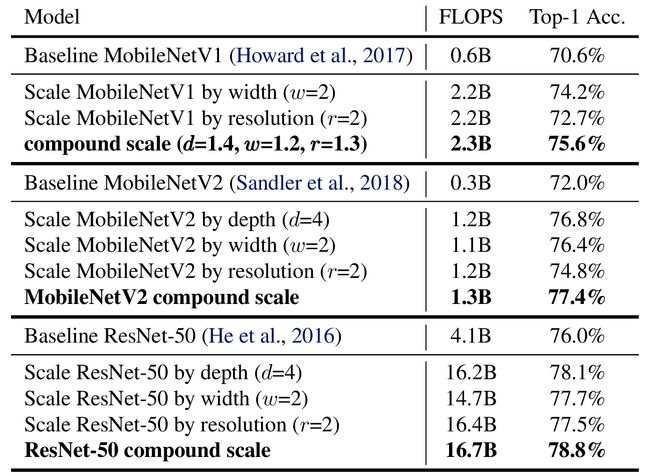
(1)在MobileNets和ResNets中,与其他单一维度的缩放方法相比,复合缩放方法精度提高了;
(2)本文提出的EfficientNet比其他网络表现更好。