Online learning系列：从RDA、FOBOS到FTRL

前言

在一般的机器学习任务中，往往是通过batch的训练方法进行离线训练，然后线上进行预测，通常离线模型更新的时间在1天以上，这就使得模型不能及时学到实时的特征；另一方面，如果要进行实时训练的话，需要特征尽量稀疏，因为大规模的机器学习往往伴随着大量的参数，如果做不到特征计量稀疏的话，实时预估时延就会很大，这个时候就要用到online learning的一些方法，其目的是在提高训练参数稀疏性的同时，也提高训练精度。

梯度下降法

最原始的也是最简单的参数更新的方法是梯度下降法，即：
$$W_{(t+1)}=W_t-{\eta }_t\ast {\ell }_W(W_t,Z)$$
当然这里可以加batch进行梯度更新，这种更新方法存在的问题就是很难产生稀疏的特征，不适合online learning的场景。

l1正则

在机器学习任务中，我们知道，可以加l1正则来使得特征变的稀疏，如：
$$W_{(t+1)}=W_t-{\eta }_t\ast ({\ell }_W(W_t,Z)+\lambda sgn(W_t))$$这样能保持参数更新尽量趋近0，这种方法可以一定程度上增大稀疏性

截断梯度法TG

梯度截断法是在l1的正则基础上提出的一种变体，其更新方式是：
$$W_{t+1}=T_1(W_t,{\eta }_t\ast ({\ell }_W(W_t,Z),{\eta }_t\ast \lambda sgn(W_t))$$其中$T_1$的表达式是
$$T_1(v,a,\theta )=\{\begin{array}{rl}& max(0,v-a)ifv\in [0,\theta ]\\ & min(0,v+a)ifvin[-\theta ,0]\\ & votherwise\end{array}$$
TG和L1正则的对比图：

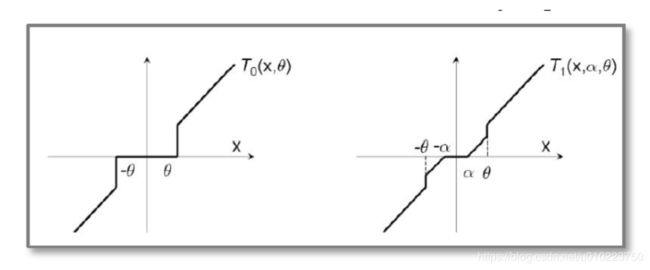
可以看出的是，TG比L1正则更加柔和了一点，但是这两种方法还是非常的“武断”和“粗糙”

Regularized Dual Averaging Algorithm(RDA)

这里就有人提出了新的在线学习参数更新方法，特征权重更新方式是：$$W_{t+1}=argmi{n}_w\{\frac{1}{t}\sum _{i=1}^t{g}_i\cdot w+\psi (w)+\frac{{\beta }_t}{t}{h}_{(}w)\}$$
其中$\psi (w)$是正则项，$h_w$是一个严格凸函数。

RDA的l1正则化

这里我们讨论RDA的l1正则化，即更新方式为：
$$W_{t+1}=argmi{n}_w\{\frac{1}{t}\sum _{i=1}^t{g}_i\cdot w+\lambda |w|+\frac{\gamma }{2\sqrt{t}}|w{|}_2^2\}$$
现在我们去求解这个更新值
令 $$\overline{g_{1:t}}=\frac{1}{t}\sum _{i=1}^t{g}_i$$
则原式变为：
$$W_{t+1}=argmi{n}_w\{\overline{g_{1:t}}\cdot w+\lambda |w|+\frac{\gamma }{2\sqrt{t}}|w{|}_2^2\}$$
这里有结论：$\overline{g_{1:t}}\cdot w\le 0$且$sgn(\overline{g_{1:t}})=-sgn(w)$
证明：假如$w_i$是上面的最优解且$\overline{g_{1:t}}\cdot w>0$,那么可以肯定的是，存在$w=0$能够使得上式最优，这个和假设矛盾，因此可以证明$\overline{g_{1:t}}\cdot \le 0$,当$\overline{g_{1:t}}=0$的时候，显然$w=0$
有了上面的结论，将求解式变成：
$$\begin{gathered} argmi{n}_w(\frac{\gamma }{2\sqrt{t}}\{w+\frac{\sqrt{t}}{\gamma }(\lambda sgn(w)+\overline{g_{1:t}}){\}}^2+c) \\ =argmi{n}_w(\frac{\gamma }{2\sqrt{t}}\{w+\frac{\sqrt{t}}{\gamma }(-\lambda sgn(\overline{g_{1:t}})+\overline{g_{1:t}}){\}}^2+c) \\ =argmi{n}_w(\frac{\gamma }{2\sqrt{t}}\{w+\frac{\sqrt{t}}{\gamma }sgn(\overline{g_{1:t}})(-\lambda +|\overline{g_{1:t}}|){\}}^2+c) \end{gathered}$$

其中$c$为常量,可以得出：
$$W_{t+1}=\{\begin{array}{rl}& 0if\overline{g_{1:t}}<\lambda \\ & -\frac{\gamma }{\sqrt{t}}(-\lambda sgn(\overline{g_{1:t}})+\overline{g_{1:t}})otherwise\end{array}$$
RDA其实是考虑了历史的梯度关系，在更新当前的梯度的时候，会考虑历史上的更新梯度对当先的影响。

Forward Backward Splitting

FOBOS的方式和RDA有所不同，其参数更新方式是：
$$\begin{gathered} W_{t+0.5}=W_t-{\eta }_t\ast g_t \\ w=argmi{n}_w\{\frac{1}{2}|w-W_{t+0.5}{|}_2^2+{\eta }_{t+0.5}\psi (w)\} \end{gathered}$$
第一个式子是求当前的梯度下降更新值，第二个式子是求FOBOS更新值，其本意是希望$W_{t+1}$不会距离梯度下降值太远，同时加入正则项保持其稀疏的特性

FOBOS的l1正则化

FOBOS-l1的更新公式是：
$$w=argmi{n}_w\{\frac{1}{2}|w-W_{t+0.5}{|}_2^2+\hat{\lambda }|w|\}$$
其中$\hat{\lambda }={\eta }_{t+0.5}\ast \lambda$令$W_{t+0.5}=v_t$
和RDA一样反证法可以得出 $w\cdot v_t\ge 0$
求解式子可以得出:
$$\begin{gathered} \frac{1}{2}(w-(v_t-\hat{\lambda }sgn(w)){)}^2+c \\ =\frac{1}{2}(w-(v_t-\hat{\lambda }sgn(v_t)){)}^2+c \end{gathered}$$
因此可以得出结论：
$$W_{t+1}=\{\begin{array}{rl}& 0if{v}_t\le \hat{\lambda }sgn(v_t)\\ & -\hat{\lambda }sgn(v_t)+v_{t}otherwise\end{array}$$
整理一下可以得到$$W_{t+1}=max(0,v_t-\hat{\lambda }sgn(v_t))$$

Follow the Regularized Leader(FTRL)

ftrl总体上是结合了RDA和FOBOS的优点，其参数更新方法如下：
$$W_{t+1}=argmi{n}_w(G_{1:t}\ast w+{\lambda }_1||w|{|}_1+\frac{1}{2}\sum _{s=1}^t{\sigma }_s||w-w_s|{|}_2^2+{\lambda }_2\frac{1}{2}||w|{|}_2^2)$$
其中$$G_{1:t}=\sum _{s=1}^t{g}_s$$也就是前面时刻梯度的和
$${\sigma }_{1:t}=\frac{1}{{\eta }_t}$$其中${\eta }_t$是当前时刻的学习率
将上面的式子改写成：$$W_{t+1}=argmi{n}_w\{(G_{1:t}-{\sigma }_s{w}_s)\cdot w+\frac{1}{2}(\frac{1}{{\eta }_t}+{\lambda }_2)||w|{|}_2^2+{\lambda }_1||w|{|}_1+c\}$$
令$$z_t=G_{1:t}-\sum _{s=1}^t{\sigma }_s{w}_s$$有:$$z_t=z_{t-1}+g_t-{\sigma }_t{w}_t=z_{t-1}+g_t-(\frac{1}{{\eta }_t}-\frac{1}{{\eta }_{t-1}})w_t$$
原式可以写成：
$$argmi{n}_w\{z_{t}w+\frac{1}{2}(\frac{1}{{\eta }_t}+{\lambda }_2)||w|{|}_2^2+{\lambda }_1||w|{|}_1\}$$
按照之间的求解方法，可以知道$z_{t}w\le 0$，将其改写成：
$$W_{t+1}=argmi{n}_w\{\frac{1}{2}(\frac{1}{{\eta }_t}+{\lambda }_2)(w+\frac{1}{2}(\frac{1}{{\eta }_t}+{\lambda }_2{)}^{-1}(-{\lambda }_{1}sgn(z_t)+z_t{)}^2+c)\}$$
由此可以得到：

$$W_{t+1}=\{\begin{array}{rl}& 0if{z}_t\ge {\lambda }_{1}sgn(z_t)（即|z_t|\ge {\lambda }_1）\\ & -\frac{1}{2}(\frac{1}{{\eta }_t}+{\lambda }_2{)}^{-1}(-{\lambda }_{1}sgn(z_t)+z_t)otherwise\end{array}$$
我们令$${\eta }_t=\frac{\alpha }{\beta +\sqrt{{\sum }_{s=1}^t(g_s{)}^2}}$$
可以得到ftrl的更新步骤：

关于ftrl使用的经验

1. 对训练数据顺序敏感，对正负比例敏感
2. 因为ftrl参数更新的时候，会考虑到历史的参数，如历史的梯度和历史的参数更新值，因此ftrl对数据顺序和正负样本个数非常敏感，ftrl更新公式的$G_{1:t}w$考虑的是历史的梯度更新值，而后面$||w-w_s|{|}_2^2$考虑的是历史的参数更新值，因此可以对数据分布不均的进行适当的梯度$g_i$或者${\sigma }_s$进行打压，能够一定程度上起到upsampling或者downsampling的效果
3. 参数beta和alpha根本上是在调整学习率，其中alpha越大学习率越大，beta影响的是开始学习率，beta越大初始学习率越小（论文建议是1）

FTRL实践

可以参考这位大神的代码里面附了详细的实现

——记于北京