社区发现有啥鸟用No.14

当当当，同学们说要听算法，那今天就说说算法，关于社区发现的一系列算法。

最近一段时间工作上使用到了社区发现，虽然只是小小一部分。但是呢，工作量还是不小的，在网上找了很多的资料，也做了很多的研究性工作，看了非常多的paper，也做了一点小改进。那么来开始总结一下社区划分究竟怎么做，目前有哪些主流的做法以及他们的原理是什么。

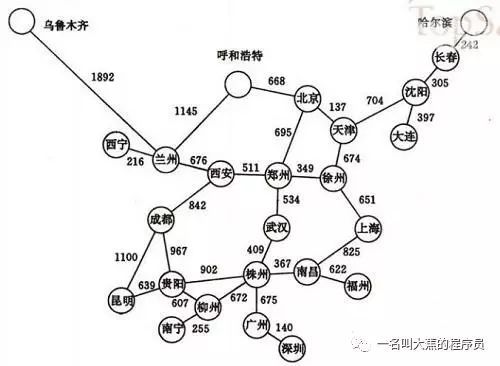
图，这里不是指图片的图喔。而是一个名字叫图的数据结构类型，由点和边构成。在我们的世界中怎么理解它呢？比如我们定义了北京，上海，广州为点，那么北京上海广州之间的所有交通形式都可以描述为边，比如高速公路是一条边，飞机航线是一条边，非常非常多的边和点加起来，就构成了地图，在数据结构中，叫做图。

图最基本的结构可以只有两个点，一条边，也就是我们现在程序猴的生活。公司<---->宿舍。最复杂但是最形象的可以看看现在的互联网，是由非常多的路由器交换机为点，电线光纤等为边的图。我们的大脑，可以看成是非常多的神经元为点，神经元间的突触为边的图。

说完这个大家应该对图有一个基本的了解了。那么实际生活中对于图有什么算法上的应用呢？

当然有了。比如对于我们每天的快递和外卖配送问题，有鼎鼎大名的一系列车辆路径问题VRP（Vehicle Routing Problem），可以使得配送员走最短的路程，优化效率。比如朋友圈和社区发现，通过对于社交网络的划分，来发现各种小社区，对他们进行精准推送。以及路由分配算法，也属于最短路径的一种。

总得来说，图算法的主要贡献在于，定义了一个复杂的非数组型结构，来对生活中的很多类似的问题进行简化模拟，进而寻找出能够优化现实中效率的算法。

说了这么多社区发现又是什么玩意？

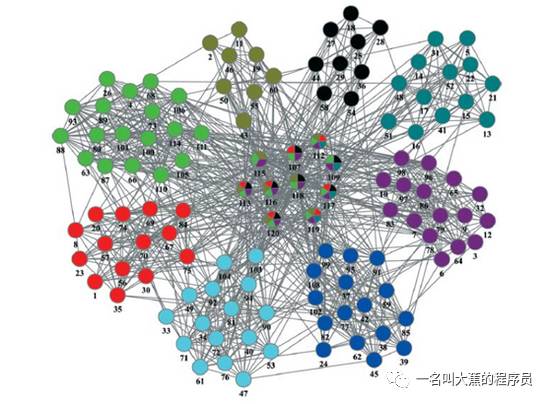
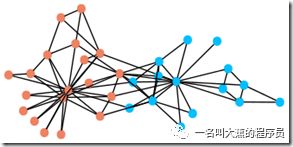
社区划分就是在一个比较大图里，对它们进行区分，进而找到相同社区里面的点相对靠近，不同社区的点相对疏远，这样的算法。

很多人听到这就蒙了，啥玩意，不要慌，你们手中的k-means，也就是k均值算法不就是社区发现的一种吗？无监督地找出k个能够划分的类别。这里就不深入谈它了，我们的重点还是图数据结构中的社区发现。

目前来说，社区发现中只有两种主流的做法。第一种是cut，也就是划分，把无关联的边去掉，进而取到核心的社区。第二种是gather，也就是聚合，将关联性比较大的顶点聚集起来，关联性较小的顶点剔除出去。

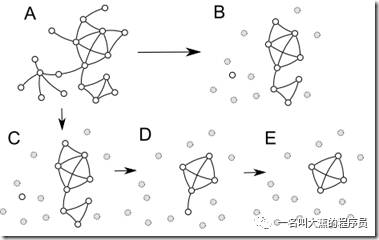
最简单的算法k-core decomposition，就是对图中的所有顶点进行判定，若度小于K，则将该点和所有关联的边从图中删除，然后再进行下一轮迭代，直到图中所有的顶的度都大于K。

LOOP

        （1）找到小于K的点

        （2）删除步骤1找到的点和边

        （3）继续进行步骤1，若找不到符合条件的点则结束

END

这个算法有什么问题呢?最终得到的图结构非常简单，但是也非常零散，但是能够找到非常非常核心的组织中心。

Label Propagation Algorithm标签传播算法，是属于第二种，是基于点聚合的一个算法。每个顶点在开始的时候都设立自己的标签，然后向所有的邻居进行广播。每个顶点在接收到广播的时候呢，将收到的最多的标签作为自己的标签，进行下一轮的迭代。

初始化：（1）顶点标签

LOOP

        （2）发送自己的标签

        （3）接收标签

        （4）将最大标签作为自己的标签

        （5）继续进行方法2，直到达到最大迭代次数。

END

这个算法的时间复杂度是线性的，无论多么复杂的图，一般在五次以内都能够比较准确地发现社区。但是有什么问题呢？结果会震荡。在星型网络和长链型网络中，结果会不断震荡。这又给我们带来了思考，是不是有更优的算法？答案是有的。

在现实生活中，每个人都可能属于不同的社区，而LPA算法只能将顶点划分一个社区内，而且结果会震荡。接下来介绍的SLPA算法。Speaker Listener Label Label Propagation Algorithm。主要是LPA算法的升级版，改进点就在于，顶点在发送和接收的时候都可以有规则，而顶点的标签也从一个标签替换为一个Array，可以进行单顶点多社区的划分。

初始化：（1）顶点标签

LOOP

        （2）根据规则发送标签

        （3）接收标签，将标签以一定的规则追加到自己的标签中

        （4）继续进行方法2，直到达到最大迭代次数。

END

        （5）对结果进行解析，自行决定单顶点社区的个数。

这个结果不会有震荡，时间复杂度也跟LPA是一样的，只是空间复杂度上从O(N)变为O(kN)，还算可以接受。

SLAP社区划分的结构还算可以接受，那还有没有呢？答案是有的。

HLAP，就是混合型LAP，王婷博士的成果，这个结果算最好。这个HLAP主要是基于二分图的一个算法，跟LAP思想差不多。主要流程是这样的。

初始化：（1）只初始化图的一边

LOOP：

        （2）发送自己的标签

        （3）接收标签

        （4）将最大标签作为自己的标签

        （5）继续进行方法2，直到达到最大迭代次数。

END

这个方法对于二分图效果较好。

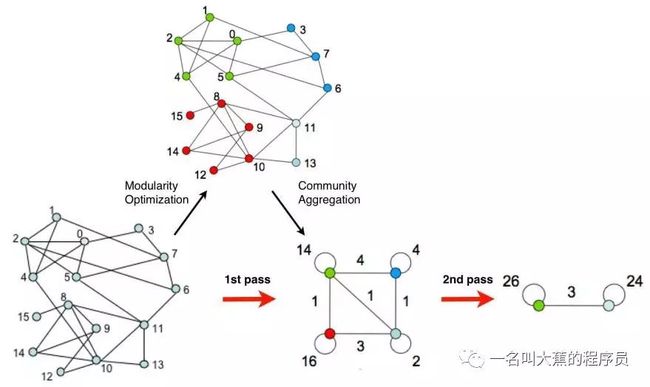
几乎讲完了LPA系列的算法，其实还有另外一个系列，也就是基于Modularity的一些算法，也就是要找到quan'qquan全局模块度最大的最优解，或者局部最优解。这个系列的算法普遍时间复杂度比较高。

模块度（modularity）指的是网络中连接社区结构内部顶点的边所占的比例，减去在同样的社团结构下任意连接这两个节点的比例的期望值

这类算法的过程大概如下。

    初始化：（1）将各个顶点划分到不同的社区

    LOOP

    （2）尝试将自己划分到所有有关联的社区中

    （3）计算△Q，并将自己添加到模块度增加最大的社团中

    （4）重复步骤2直到模块度不再增加

    END

相当多的算法都是在计算模块度这里下功夫。

而有的算法从局部最优变为全局最优，不再看本社团的模块度，而是从全局上进行优化，计算复杂度增高，算法收敛比较慢，但是划分结果比较理想。好了讲一半，下次继续讲，手好酸妈蛋。

欢迎大家留言交流。

感谢大家一直的支持，随便来点都好开心。