一步一步带你拆解PageRank算法
一般描述
PageRank算法是谷歌创始人佩奇和布林的博士论文中提出的算法，然后他们利用这个算法成立了谷歌，一个当前（2019年7月）市值最高的公司之一。换句话讲，人类历史上最厉害的算法或许不知道是哪个，但是最有“钱途”的算法无疑就是PageRank了。
PageRank算法提出来之前，人们在互联网上浏览网页，基本上只有三种途径，一种是朋友的推荐或者自己的收藏夹，或者雅虎这样的黄页，在某种意义上雅虎黄页可以算作雅虎的推荐或者收藏夹，第二种是通过一个网页内的超链接跳转到其他网页，还有第三种是通过关键词匹配（PageRank算法之前的搜索引擎）来展示备选网页。无论哪一种方式都有缺陷，最关键的缺陷是扩展性几乎为0，由于互联网的开放性和自由性，每天都有无数的网页创建和关闭，靠人力维护收藏夹（雅虎黄页）的成本太高难以为继，如果通过关键词展示网页又无法将重要的网页放在列表的前面让上网者重点关注。
PageRank算法正是为了解决网页的开放性和人们寻找信息的迫切性之间的矛盾提出来的算法，PageRank算法通过网页之间的拓扑结构给每个网页节点打分来给予每个网页不同的权重，然后在符合用户搜索关键词的网页列表中按照重要性从高到低展示出来。由于PageRank算法是无监督的挖掘算法，所以其人工标注的成本为0，也不需要特别维护，所以特别适合互联网这样的开放领域。
下面我们就来讲一讲PageRank算法到底是如何给网页打分的。
朴素的原始想法
一个网页，通常会有其他的网页的链接以帮助浏览者拥有更好的阅读体验，也会有别的网页引用其地址。于是我们有了一个朴素的想法，一个网页，会把的得分传递给他所引用的页面。这里我们做一个假设，假设一个浏览者，会随机的打开页面中的一个链接进入下一个页面，这样每一个网页会把浏览者传递给其引用的网页，我们把网页得分就想象成浏览者的数量。
像上面描述的那样，我们有了网页得分的公式：
如果结点1到结点2之间没有边相连，则结点1无法将得分传递给结点2，即结点2的PR得分公式中结点1的系数为0。
例如：
公式的矩阵表示
我们把所有网页得分列在一起组成列向量，记做P，并把公式右边的系数组成的矩阵记作T，这样，我们就可以把网页公式的写作：
P = T P P = TP P=TP
迭代求解
要求出网页的最终得分，我们可以使用迭代方法，迭代的方式可以有两种，
- 一种是一个更新一个网页得分，然后立刻将其得分更新；
- 一种是利用矩阵表达式，所有的变量一同更新。
下面展示以下这两种更新方式的区别：
两种更新方式各有优缺点，第一种方式收敛速度更快，但是无法并行；第二种方式可以并行计算各个节点的得分，但是收敛速度慢。
当然，我们迭代时，并不总是需要求出收敛值，有时候只需要迭代一定次数就可以得到要求了，因为PageRank所求的时网页的打分，本身就不是需要精确值的过程（因为网络结构时开放的，每时每刻都在变化中）。
很显然，我们可以结合两种方法的优点，也就是每次批量更新一些结点而不是更新一个或者全部。
除了迭代法外，我们观察矩阵迭代公式，发现收敛点P是矩阵T的特征值为1的特征向量，我们可以使用求特征向量的方法求解P值。
马尔科夫过程解释
在使用矩阵公式迭代时，我们可以将迭代过程看作一个马尔科夫过程，X0->X1->X2->…->Xk->…可以看作一个马尔科夫过程，P0是假设一开始浏览处在每个页面的概率分布，T是状态转移矩阵，Xk是第k次转移后浏览者所处的页面，Pk=P(Xk)是Xk的分布列。
想像一个画面，一个人坐在电脑前，他按照初始概率P0随机打开了一个页面，然后他随机点开一个该页面的里面的超链接跳转到另一个页面，如此重复k次，其所处的页面的分布列即是Pk。
一个人浏览网页当然不是如此随机，但是成千上万的人浏览网页，其总体行为表现就可以看成是随机的了，这也是PageRank算法之所以有效的原因。
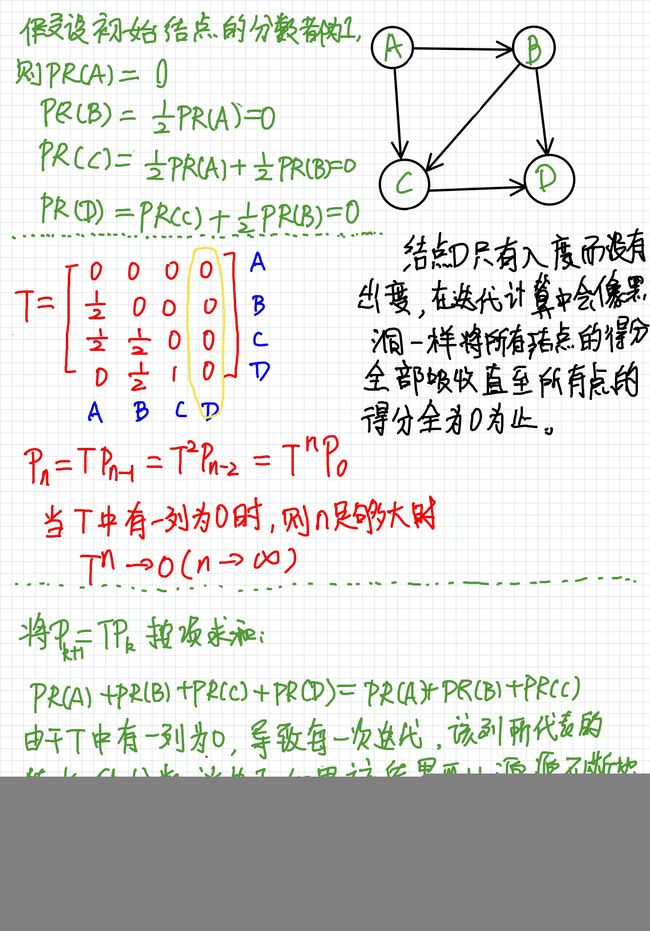
“黑洞效应”
我们把出度为0的顶点称作终止点，终止点会把所有的其他节点的PR分吸收，导致所有指向终止点的PR分都变为0，就像黑洞一样吞噬掉所有的PR，终止点就是那个黑洞，只吸不吐。
例如：
为避免黑洞效应，我们可以在图中删除终止点并将终止点的PR得分设置为0。但是删除终止点会产生新的终止点，所以需要递归的删除终止点直到图中没有终止点。
可是另一方面，删除终止点的方法一点也不符合直觉。想象以下存在一个“傲娇”的网页，他没有超链接指向任何网页，但是由于他的重要性，有很多别的网页指向他，但由于该网页的没有出链导致其时一个终止点，其PR分为0，显然这是不合理的。并且这种现实中并不少见。
闭环陷阱
除了终止点会吸收网络的PR外，闭环也会吸收网络其他部分的PR值。我们把存在大于等于一个边且没有指向网络其他部分的结点的连图子图称作“闭环”。故名思意，就是封闭的环，环的内部“自给自足”，不与外界交换信息，如同“闭关锁国”一般。
例如下面这种情况：
“闭环”会把非闭环部分的结点的PR得分全部变为0，然后再在自己内部分配分配PR值，跟吸星大法似的。而浏览者犹如陷入陷阱，在闭环中无法脱身。
更需要说明的是，闭环在互联网可以说非常普遍，例如我可以写一个网页，然后自己指向自己，或者写N个网页，然后像印度的衔尾蛇一样，循环指向，无穷无尽。
解的不稳定性
除了“终止点问题”和“闭环陷阱”，上述的迭代公式还有下面的问题：
解空间的维度大于1
当网络结构图中出现多个“闭环”，方程的解构成的空间维度就会大于1，如：
理论上，网络存在多少个"闭环"，其解空间的维度就有多少。
周期解
方程P=TP没有稳定解，只有周期解，如：
以上两种现象我把它们归类为解的不稳定性。
终极模型
如果无法解决上述的三个问题，整个算法就无法使用，因为它不仅解决不了真实网络的问题，而且还会被黑客构造特例进行攻击，这样的算法是没有大规模应用的价值。
想象以下我们是一个浏览者，如果我们浏览到一个没有出链的网页，我们会怎么办，我们当然会在网址栏填入一个地址跳转到新的网页；当然，如果我们被一个互相调用的闭环网页群给困住，难道我们会傻傻的在网页间不停的跳来跳去？
我们肯定会关掉网页，输入一个网址进入一个新页面啊。
利用这个想法，我们将上面的浏览过程修改以下：
一个浏览者浏览网页，不仅会按照网页里的出链随机跳转到对应的页面，还有一定概率会在网址栏随机输入网址，跳转到网址对应的页面。
于是PR值的更新得公式可以表示为：
一个示例
下面会展示修改后的公式是如何跳过上面所展示的“闭环陷阱”的:
终极公式不仅会解决闭环陷阱问题，还会解决终止点问题，解的不稳定性想象。
模型的弊端
- 模型对链接一视同仁，无法区分指向站内的链接和指向站外的链接；也无法区分链接是导航链接还是广告链接或是功能链接，其对广告链接会高估；
- 模型会低估新加入网络的链接，因为新加入的链接缺少指向其的其他页面，优秀的内容如同美酒需要经过时间发酵才能让其得分变高；
- 模型是主题的无关，模型没有利用页面的内容进行计算。
一些叨叨叨
- 初始评分问题：谷歌等搜索引擎不会像上面展示的那样，把每个网页的初始评分都设置成1，而是给一些重要的网址复制一个PR值，越重要PR值越高，其余的网页/网址的PR值全部设为0，然后使用迭代公式求解其他页面的得分，且这些重要页面的PR值是不参与更新计算的；
- 收敛问题：PageRank算法在使用中并不追求达到收敛，因为一是网络是动态变化的，二是网页太多收敛消耗的时间不可抵达，所以很多时候谷歌们只是一刻不停的更新网络的拓扑结构，不停的更新网页的PR值，这跟真实世界一样，是连续的动态的；
- 攻击问题：由于PageRank算法是公开的，所以为了在搜索引擎中提高排名，SEO应运而生，通过透析PageRank的原理，SEO工程师构造攻击手段，提高自己的PR得分，为了打击SEO工程师们对真实排名干扰，谷歌们会在PageRank算法的基础上使用更多的技术和算法来优化最终的排名列表，这是搜索引擎的核心竞争力之一；
- 谷歌的产品逻辑：停留在谷歌上的时间越短越好，用完即走。用户打开谷歌，搜索一个关键词，打开一个页面即离开谷歌，用户呆在谷歌上的时间越少，说明谷歌真的将用户需要的内容展现在了最前面，如果用户需要翻页等操作才能找到需要的页面，说明谷歌做得还不够好。这既不同于娱乐性产品追求用户的在线时长，也不同于有些产品为了追求PV故意增加用户的操作步骤，更不同于线下大部分商场会故意把超市等人流量大刚需的店铺入口设置的七拐八绕，就是为了给别的店铺增加流量。
应用产景
根据上面的介绍，我们可以得出可以应用PageRank算法需要的两个条件：
- 网络的结点在一定意义上是等价的，例如都是网页，不能有些是书籍有些是读者；
- 网络的结点之间应该有一定的链接，不能都是相互独立的，例如天上的星星。
这里我举例几个应用产景：
PaperRank
给论文打分，引用别的论文是入链，被别的论文引用是出链。被引用次数越多得分越高，引用其的论文得分越高，被引用的论文得分也就越高。
SocialRank
微博或者推特这样的社交性网站上用户的影响力，粉丝是出链，关注是入链。大V不仅要比粉丝数量，也要比用户质量。一个大V粉比一万个僵尸粉的权重可能更大。
MoneyRank
像支付宝这样的金融平台，可以将钱的流向视作边，计算出每个用户的金钱影响力。流入的越多越散，说明其的敛财能力越强。
供应链
类似上述所讲的MoneyRank，用金钱的流向作为客户和供应商之间的边，用销售额作为边的权重，这样就可以给每个公司打分，衡量其在产业链中的地位。
参考文献
[1] 深入浅出PageRank算法
[2] The PageRank Citation Ranking:Bringing Order to the Web
[3] PageRank算法
[4] PageRank算法原理及优缺点
[5] The PageRank Algorithm