FxLMS算法

FxLMS算法

版权声明：本文为博主原创文章，转载请附上博文链接！

1 前言

在前一篇中我们简要介绍了有源噪声控制的系统构成和基本应用，现在来详细介绍有源噪声控制中最常用的算法，FxLMS算法。如前文所说，有源噪声控制与传统的自适应信号处理最根本的区别就是多了次级通路。这里的Fx即filtered-x信号，为参考信号经过次级通路滤波得到的。
FxLMS算法为有源噪声控制的基准算法，实现简单且运算量小，它源于Widrow所提出的LMS算法。1980年，在通用电气公司工作的Morgan D. R首先推导了这一算法。1981年，在贝尔实验室工作的Burgess在研究管道噪声控制时提出了这一算法，并命名为FxLMS算法。

2 单通道FxLMS算法

如图中所示的有源噪声控制模型。

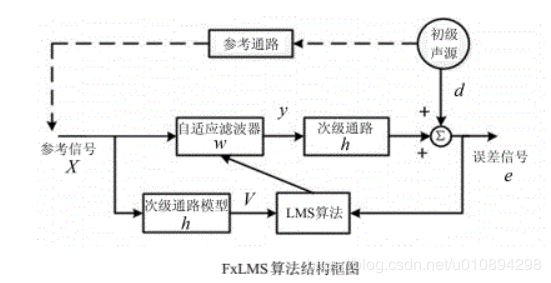控制滤波器长度为$L$，次级通路长度为$M$。参考信号为$x(n)$，在误差传感器处，期望信号为$d(n)$，抵消信号$s(n)=y(n)\ast h(n)$，它是滤波器输出$y(n)$经过次级通路后得到的响应。
设第$n$时刻滤波器权系数和参考输入分别为
$$\mathbf{w}(n)=[w_1(n),w_2(n),...,w_L(n){]}^T$$$$\mathbf{x}(n)=[x(n),x(n-1),...,x(n-L+1){]}^T$$

则滤波器的输出为$$y(n)={\mathbf{x}}^T(n)\mathbf{w}(n)$$如果认为在$L$个采样点内滤波器权系数基本保持不变，那么$$s(n)={\mathbf{v}}^T(n)\mathbf{w}(n)$$式中$\mathbf{v}(n)$即为滤波-x信号。有$$\mathbf{v}(n)=x(n)\ast h(n)$$误差传声器接收到的信号为$$e(n)=d(n)+s(n)$$

根据最小均方误差准则，有源控制系统的目标函数为$$J(n)=E[e^2(n)]$$根据最速下降法原理，有$$\mathbf{w}(n+1)=\mathbf{w}(n)-2\mu e(n)\mathbf{v}(n)$$以上即为单通道前馈FxLMS算法的原理，可以看到控制器采用横向FIR滤波器，实现简单，因此在有源噪声控制中被广泛采用。在很多情况下，利用单通道系统并不能在较大的范围内形成静区，因此需要采用多通道有源噪声控制系统，这就需要采用多通道算法。多通道算法在原理上是相同的，只是运算量大幅度增加。

3 多通道FxLMS算法

设系统中有$I$个参考信号，$J$个次级声源，$K$个误差传感器。单个横向滤波器长度为$L$，次级通路长度为$M$。为了表述清晰，我们采用和单通道算法同样的思路。自适应滤波器共有$IJ$个，单个滤波器权系数为$${\mathbf{w}}_{ij}(n)=[wij(1),wij(2),...wij(n){]}^T$$第$i$个参考信号为$${\mathbf{x}}_i(n)=[x_i(n),x_i(n-1),...x_i(n-L+1){]}^T$$
则第$j$个次级声源的输出为$$y_j(n)=\sum _{i=1}^I{\mathbf{x}}_i(n){\mathbf{w}}_{ij}(n)$$第$k$个误差传感器处的抵消信号为$$s_k(n)=\sum _{j=1}^J{y}_j(n)\ast h_{jk}$$则误差信号为$$e_k(n)=d_k(n)+s_k(n)$$根据最小均方误差准则，多通道控制系统的目标函数为$$J(n)=\sum _{k=1}^{K}E[e_k^2(n)]$$根据最速下降法原理，有$${\mathbf{w}}_{ij}(n+1)={\mathbf{w}}_{ij}(n)-2\mu \sum _{k=1}^K{e}_k(n){\mathbf{v}}_{ijk}(n)$$式中${\mathbf{v}}_{ijk}(n)$为第$i$个参考信号经过第$j$个次级声源到第$k$个误差传感器之间的次级通路后产生的滤波-x信号，即$${\mathbf{v}}_{ijk}(n)=x_i(n)\ast h_{jk}(n)$$
算法运算量如表中所示

算法运算步骤	乘加次数
计算滤波器输出	$IJL$
计算滤波-x信号	$IJKM$
权系数迭代	$IJKL$

4 FxLMS算法编程

为了进一步理解FxLMS法，作者在这里进行了Matlab编程，如果您有兴趣，请参考有源噪声控制FxLMS算法。程序为Matlab函数文件，不可以直接运行，需要您自行输入参数。下面为具体说明。

X(1:L)'*W   //计算滤波器输出
X(1:M)'*Hs_m    //计算滤波-x信号
//滤波权系数迭代
for j=1:J
    W(:,j)=W(:,j)-u(j)*F(:,(j-1)*K+1:j*K)*e(:,n);
end

另外请参考宽带与窄带信号有源噪声控制，为Matlab中.m文件，可以直接运行。初级噪声为宽带与窄带复合噪声。运行结果为

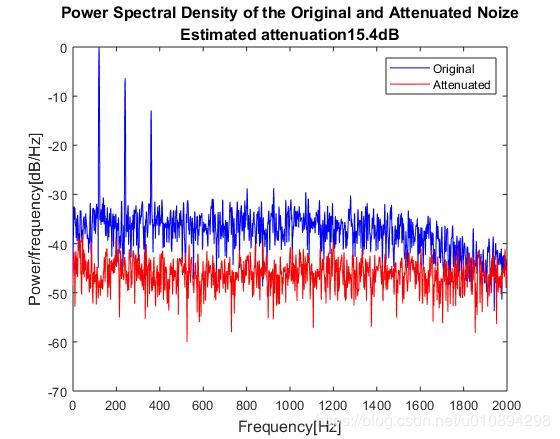
蓝色为降噪前，红色为降噪后。