并行排序

个人博客网址：http://hyperparameter.cn/

并行排序算法是计算机并行计算能力大大发展之后，为了提高排序效率而提出的算法。

原有的的排序算法都是给定了数据再进行排序，排序的效率很大程度上取决于数据的好坏，例如快速排序、归并排序。并行排序则是一类完全不同的排序方法，它的所有比较操作都与数据无关。

并行排序的表示方式是排序网络，其主要构件就是Batcher比较器，通过组合比较器构建网络来完成排序功能。Batcher比较器指在两个输入端给定输入x,y，再在两个输出端输出最大值$\text{max}\{x,y\}$和最小值$\text{min}\{x,y\}$。

传统排序算法网络

实际上，传统的某些排序算法（无条件比较的排序算法¹）也可以用网络的形式表示，例如归并排序和快速排序就无法通过比较器构成的电路网络表示，因为无法预先知道后面的条件交换操作会在什么位置进行，换种说法就是，比较器构成的电路网络中必须不考虑输入就确定结构。

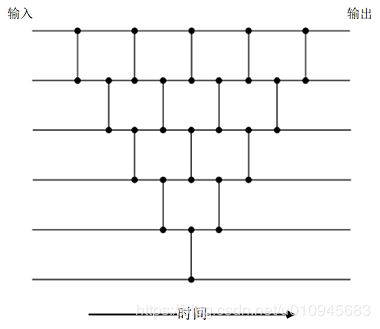
以冒泡排序举例，其核心是依次得出序列中的最值，其网络结构如下图所示（经调整过的冒泡排序网络，因为第$n$轮冒泡和第$n-1$轮冒泡在相差两个时间步后不再相互依赖，因此有一定的流水线并行性）。但是在并行硬件的背景下，可以看出这种排序算法仍有很大的改善空间（网络中的空白很多）。这是由于这类排序依赖于邻近数据的相对大小关系，不能很好地利用并行计算的资源。因此最直接的改良思路就是打破排序过程中数据间的依赖性，由此得到了奇偶合并网络和双调排序网络。

冒泡排序网络

奇偶合并网络

首先考虑奇偶排序方法，该方法主要有三个步骤：

1. 选取所有奇数列的元素与其右侧相邻的元素进行比较，将较小的元素排序在前面；
2. 选取所有偶数列的元素与其右侧相邻的元素进行比较，将较小的元素排序在前面；
3. 重复前面两步，直到所有序列有序为止。

这是最基础的奇偶排序算法，其网络表示如下，该方法的平均时间复杂度为$O\left(n\log n\right)$

奇偶排序算法 ²

奇偶合并网络就是结合了两个部分：归并排序得到两个有序的子序列，以及最后对两个子序列的合并过程。如下图所示，两个蓝色方框内依次完成归并排序的两层得到两个有序的子序列。最后的合并过程（后面一个红色框），则是首先对所有的奇数项和偶数项分别递归地合并，然后在排序后的第i个偶数项和第i+1个奇数项之间设立Batcher比较器分别进行最后的调整。

平均和最差时间复杂度都是$O\left({\log }^2(n)\right)$，空间复杂度则是$O\left(n{\log }^2(n)\right)$。奇偶归并网络的Python实现如下，

def oddeven_merge(lo, hi, r):
    step = r * 2
    if step < hi - lo:
        yield from oddeven_merge(lo, hi, step)
        yield from oddeven_merge(lo + r, hi, step)
        yield from [(i, i + r) for i in range(lo + r, hi - r, step)]
    else:
        yield (lo, lo + r)

def oddeven_merge_sort_range(lo, hi):
    """ sort the part of x with indices between lo and hi.

    Note: endpoints (lo and hi) are included.
    """
    if (hi - lo) >= 1:
        # if there is more than one element, split the input
        # down the middle and first sort the first and second
        # half, followed by merging them.
        mid = lo + ((hi - lo) // 2)
        yield from oddeven_merge_sort_range(lo, mid)
        yield from oddeven_merge_sort_range(mid + 1, hi)
        yield from oddeven_merge(lo, hi, 1)

def oddeven_merge_sort(length):
    """ "length" is the length of the list to be sorted.
    Returns a list of pairs of indices starting with 0 """
    yield from oddeven_merge_sort_range(0, length - 1)

def compare_and_swap(x, a, b):
    if x[a] > x[b]:
        x[a], x[b] = x[b], x[a]

双调排序网络

1968年，肯特州立大学的计算机教授Kenneth Batcher设计出一种基于比较单元的电路，可以用$0.5{\log }_2^n\cdot ({\log }_2^n+1)$并行时间步完成长度为$n$的序列排序，并命名为双调合并网络（bitonic merger）。其中，双调序列定义为一个先单调递增再单调递减（或者先单调递减再单调递增）的序列。即存在一个$0\le k\le n-1$，使得$<a_0,a_1,\dots ,a_{k-1}>$为升序序列，$<a_k,a_{k+1},\dots ,a_{n-1}>$为降序序列。

从以上定义可以推出双调序列具有的一个特点，即：如果$n$为偶数，且$<a_0,a_1,\dots ,a_{n/2-1}>$为升序序列，$<a_0,a_1,\dots ,a_{n/2-1}>$为降序序列，则以下两个序列都是双调序列，

$$S_1=<\min \left(a_0,a_{n/2}\right),\min \left(a_1,a_{n/2+1}\right),\dots ,\min \left(a_{n/2-1},a_{n-1}\right)>$$

$$S_2=<\max \left(a_0,a_{n/2}\right),\max \left(a_1,a_{n/2+1}\right),\dots ,\max \left(a_{n/2-1},a_{n-1}\right)>$$

借助以上推论可以得到双调归并排序的算法，示例如下图所示，

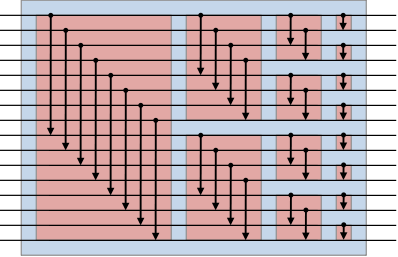
上述归并排序算法的电路网络可以表示如下图（16路输入），

那么现在就有一个问题是如何得到最初的双调序列（初始序列），这个部分就是通过下图的红框部分完成的，再拼接上双调归并排序的部分，可以看出整个双调排序网络都是基于Batcher比较器搭建而成。

双调排序网络分析 ³

下面这个是一个8输入的双调排序网络示例，可以看出也是由这两个部分组成。

8输入的双调排序网络示例

考虑双调排序网络的时间复杂度，因为该方法不依赖数据特性，最差时间复杂度和最好时间复杂度都是$O\left({\log }^2(n)\right)$，空间复杂度则是$O\left(n{\log }^2(n)\right)$。

双调排序网络的Python实现如下，

def bitonic_sort(up, x):
    if len(x) <= 1:
        return x
    else: 
        first = bitonic_sort(True, x[:len(x) // 2])
        second = bitonic_sort(False, x[len(x) // 2:])
        return bitonic_merge(up, first + second)

def bitonic_merge(up, x): 
    # assume input x is bitonic, and sorted list is returned 
    if len(x) == 1:
        return x
    else:
        bitonic_compare(up, x)
        first = bitonic_merge(up, x[:len(x) // 2])
        second = bitonic_merge(up, x[len(x) // 2:])
        return first + second

def bitonic_compare(up, x):
    dist = len(x) // 2
    for i in range(dist):  
        if (x[i] > x[i + dist]) == up:
            x[i], x[i + dist] = x[i + dist], x[i] #swap

0-1原理证明

那么给定一个排序网络，如何确定它是真的能够正确地排序任意输入呢？**0-1原理（0-1 Principle）**是由计算机教授高德纳（Donald Ervin Knuth）提出来的，他在《计算机程序设计艺术》的第三卷5.3.4节：排序与选择中，提出并论证了这个原理。该原理叙述如下：

如果一个排序网络能够正确地对任何0-1序列排序，那么它就能对任意数组成的任意序列正确排序。

因此为了验证一个输入排序网络的正确性，我们不必检验所有数字构成的任意长为n的序列，而只需检验 $2^n$个0-1序列就足以验证排序网络是否能正确排序了。这篇文章通过数学归纳法证明了奇偶合并网络能够对任何0-1序列排序，也就证明了它就能对任意数组成的任意序列正确排序。¹

非2次幂输入的排序网络

需要注意的是，以上两种提到的排序网络都假设了输入是2的整数次幂，保证了排序过程中的划分完整性。但是实际中，这是很难达到的目标，为了解决这个问题，最简单的方法就是填充，通过填充值并在排序结束后剔除以满足这个条件。还有一种方法就是对排序网络进行改进以能够解决任意$n$的输入⁴

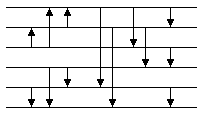
输入数据为6的排序网络设置如下，

该方法的实现如下，

public class BitonicSorterForArbitraryN implements Sorter
{
    private int[] a;
    private final static boolean ASCENDING=true;    // sorting direction

    public void sort(int[] a)
    {
        this.a=a;
        bitonicSort(0, a.length, ASCENDING);
    }

    private void bitonicSort(int lo, int n, boolean dir)
    {
        if (n>1)
        {
            int m=n/2;
            bitonicSort(lo, m, !dir);
            bitonicSort(lo+m, n-m, dir);
            bitonicMerge(lo, n, dir);
        }
    }

    private void bitonicMerge(int lo, int n, boolean dir)
    {
        if (n>1)
        {
            int m=greatestPowerOfTwoLessThan(n);
            for (int i=lo; i<lo+n-m; i++)
                compare(i, i+m, dir);
            bitonicMerge(lo, m, dir);
            bitonicMerge(lo+m, n-m, dir);
        }
    }

    private void compare(int i, int j, boolean dir)
    {
        if (dir==(a[i]>a[j]))
            exchange(i, j);
    }

    private void exchange(int i, int j)
    {
        int t=a[i];
        a[i]=a[j];
        a[j]=t;
    }

    // n>=2  and  n<=Integer.MAX_VALUE
    private int greatestPowerOfTwoLessThan(int n)
    {
        int k=1;
        while (k>0 && k<n)
            k=k<<1;
        return k>>>1;
    }

}

---

1. OI之外的一些东西：简单谈谈排序网络 ↩︎ ↩︎

2. Batcher odd–even mergesort ↩︎

3. Bitonic sorter ↩︎

4. Bitonic sorting network for n not a power of 2 ↩︎