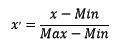特征工程 Feature Engineering（一）

数据和模型 https://blog.csdn.net/u010986753/article/details/98526886

一、特征工程（Feature Engineering）介绍

1.1 特征工程的重要性

  特征工程其本质上是一项工程活动，它的目的是最大限度地从原始数据中提取特征以供算法和模型使用。

  数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限。特征工程的最终目的就是提升模型的性能。

  特征工程的重要性：

• 特征越好，灵活性越强
• 特征越好，模型越简单
• 特征越好，性能越出色

1.2 特征工程包括哪些方面呢？

  特征工程包括：数据处理、特征选择、维度压缩三大方面的内容。

1.3 为什么要做特征工程？

  数据特征会直接影响我们模型的预测性能。选择的特征越好，最终得到的性能也就越好。
  通常实验结果取决于选择的模型、获取的数据以及使用的特征

1.4 特征工程是什么？

  当你想要你的预测模型性能达到最佳时，你要做的不仅是要选取最好的算法，还要尽可能的从原始数据中获取更多的信息。那么问题来了，你应该如何为你的预测模型得到更好的数据呢？

  想必到了这里你也应该猜到了，是的，这就是特征工程要做的事，它的目的就是获取更好的训练数据。特征工程是利用数据领域的相关知识来创建能够使机器学习算法达到最佳性能的特征的过程。

  简而言之，特征工程就是一个把原始数据转变成特征的过程，这些特征可以很好的描述这些数据，并且利用它们建立的模型在未知数据上的表现性能可以达到最优（或者接近最佳性能）。从数学的角度来看，特征工程就是人工地去设计输入变量X。

  特征工程更是一门艺术，跟编程一样。导致许多机器学习项目成功和失败的主要因素就是使用了不同的特征。说了这么多，想必你也大概知道了为什么要做特征工程，下面来说说特征工程的重要性。

二、数据处理

2.1 无量纲化

  量纲就是单位，特征的单位不一致就不能放在一起比较，可以使用数据标准化的方法来达到量纲一致的要求。不属于同一量纲：即特征的规格不一样，不能够放在一起比较。无量纲化可以解决这一问题。

  常用的数据标准化方法：

• 区间缩放法即0-1标准化是对原始数据进行线性变化，将特征值映射成区间为[0，1]的标准值中。常见的一种为利用两个最值进行缩放
  　

from sklearn.preprocessing import MinMaxScaler

#区间缩放，返回值为缩放到[0, 1]区间的数据
MinMaxScaler().fit_transform(iris.data)

• Z标准化是基于特征值的均值和标准差进行数据的标准化，标准化后的变量围绕0上下波动，大于0说明高于平均水平，小于0说明低于平均水平。标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。

from sklearn.preprocessing import StandardScaler
 
#标准化，返回值为标准化后的数据
StandardScaler().fit_transform(iris.data)

• 归一化，是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”。规则为l2的归一化公式如下：

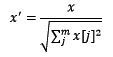
from sklearn.preprocessing import Normalizer

#归一化，返回值为归一化后的数据
Normalizer().fit_transform(iris.data)

2.2 二值化

  信息冗余：对于某些定量特征，其包含的有效信息为区间划分，例如学习成绩，假若只关心“及格”或不“及格”，那么需要将定量的考分，转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
  定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0，公式表达如下：

#使用preproccessing库的Binarizer类对数据进行二值化的代码如下：

from sklearn.preprocessing import Binarizer

#二值化，阈值设置为3，返回值为二值化后的数据
Binarizer(threshold=3).fit_transform(iris.data)

2.3 虚拟变量one-hot encoding 和 get_dummies

  虚拟变量也叫哑变量或离散特征编码，可用来表示分类变量、非数量因素可能产生的影响。
  定性特征不能直接使用：某些机器学习算法和模型只能接受定量特征的输入，那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值，但是这种方式过于灵活，增加了调参的工作。通常使用哑编码的方式将定性特征转换为定量特征：假设有N种定性值，则将这一个特征扩展为N种特征，当原始特征值为第i种定性值时，第i个扩展特征赋值为1，其他扩展特征赋值为0。哑编码的方式相比直接指定的方式，不用增加调参的工作，对于线性模型来说，使用哑编码后的特征可达到非线性的效果。

  由于IRIS数据集的特征皆为定量特征，故使用其目标值进行哑编码（实际上是不需要的）。使用preproccessing库的OneHotEncoder类对数据进行哑编码的代码如下：

  python中主要通过pandas包中的get_dummies方法进行特征变量的虚拟化，即pandas提供对one-hot编码的函数是：pd.get_dummies()。

from sklearn.preprocessing import OneHotEncoder

#哑编码，对IRIS数据集的目标值，返回值为哑编码后的数据
OneHotEncoder().fit_transform(iris.target.reshape((-1,1)))

  one-hot的基本思想：将离散型特征的每一种取值都看成一种状态，若你的这一特征中有N个不相同的取值，那么我们就可以将该特征抽象成N种不同的状态，one-hot编码保证了每一个取值只会使得一种状态处于“激活态”，也就是说这N种状态中只有一个状态位值为1，其他状态位都是0。举个例子，假设我们以学历为例，我们想要研究的类别为小学、中学、大学、硕士、博士五种类别，我们使用one-hot对其编码就会得到：

  哑变量编码（dummy encoding）直观的解释就是任意的将一个状态位去除。如上图，我们用4个状态位就足够反应上述5个类别的信息，也就是我们仅仅使用前四个状态位 [0,0,0,0] 就可以表达博士了。只是因为对于一个我们研究的样本，他已不是小学生、也不是中学生、也不是大学生、又不是研究生，那么我们就可以默认他是博士，是不是。所以，我们用哑变量编码可以将上述5类表示成：

在这里插入代码片

2.4 缺失值填充

  缺失值产生的原因：有些信息暂时无法获取（单身人士的配偶、未成年人的收入等）；有些信息被遗漏或错误的处理了

  缺失值处理方法：数据补齐；删除缺失值；不处理

  由于IRIS数据集没有缺失值，故对数据集新增一个样本，4个特征均赋值为NaN，表示数据缺失。使用preproccessing库的Imputer类对数据进行缺失值计算的代码如下：

from numpy import vstack, array, nan
from sklearn.preprocessing import Imputer

#缺失值计算，返回值为计算缺失值后的数据
#参数missing_value为缺失值的表示形式，默认为NaN
#参数strategy为缺失值填充方式，默认为mean（均值）
Imputer().fit_transform(vstack((array([nan, nan, nan, nan]), iris.data)))

2.5 数据变换

  常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征，度为2的多项式转换公式如下：

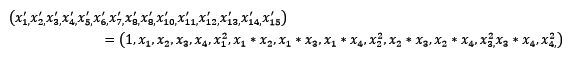  使用preproccessing库的PolynomialFeatures类对数据进行多项式转换的代码如下：

from sklearn.preprocessing import PolynomialFeatures

#多项式转换
#参数degree为度，默认值为2
PolynomialFeatures().fit_transform(iris.data)

  基于单变元函数的数据变换可以使用一个统一的方式完成，使用preproccessing库的FunctionTransformer对数据进行对数函数转换的代码如下：

from numpy import log1p
from sklearn.preprocessing import FunctionTransformer

#自定义转换函数为对数函数的数据变换
#第一个参数是单变元函数
FunctionTransformer(log1p).fit_transform(iris.data)

三、特征选择

  如何选择特征：考虑特征是否发散；考虑特征与目标相关性
  当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说，从两个方面考虑来选择特征：

• 特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
• 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。　
  　
  根据特征选择的形式又可以将特征选择方法分为3种：
• Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
• Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
• Embedded：集成法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。　　我们使用sklearn中的feature_selection库来进行特征选择。

3.1 方差选择法（filter）

  先计算各个特征的方差，根据阈值，选择方差大于阈值的特征；
  使用方差选择法，先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。使用feature_selection库的VarianceThreshold类来选择特征的代码如下：

from sklearn.feature_selection import VarianceThreshold

#方差选择法，返回值为特征选择后的数据
#参数threshold为方差的阈值
VarianceThreshold(threshold=3).fit_transform(iris.data)

3.2 相关系数法（filter）

  先计算各个特征对目标值的相关系数，选择更加相关的特征；
  使用相关系数法，先要计算各个特征对目标值的相关系数以及相关系数的P值。用feature_selection库的SelectKBest类结合相关系数来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest
from scipy.stats import pearsonr

#选择K个最好的特征，返回选择特征后的数据
#第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。在此定义为计算相关系数
#参数k为选择的特征个数
SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

3.3 卡方检验（filter）

  经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量：

  不难发现，这个统计量的含义简而言之就是自变量对因变量的相关性。用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

#选择K个最好的特征，返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)

3.4 互信息法(filter)

  经典的互信息也是评价定性自变量对定性因变量的相关性的，互信息计算公式如下：

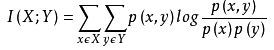  为了处理定量数据，最大信息系数法被提出，使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest
 from minepy import MINE
 
 #由于MINE的设计不是函数式的，定义mic方法将其为函数式的，返回一个二元组，二元组的第2项设置成固定的P值0.5
 def mic(x, y):
     m = MINE()
     m.compute_score(x, y)
     return (m.mic(), 0.5)

#选择K个最好的特征，返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

3.5 递归特征消除法(Wrapper)

  递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下：

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

#递归特征消除法，返回特征选择后的数据
#参数estimator为基模型
#参数n_features_to_select为选择的特征个数
RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)

3.6 模型选择法-基于惩罚项的特征选择法(Embedded)

  将建好的模型对象传入选择器，然后它会根据这个建好的模型，自动选择最好的特征值;
  使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

#带L1惩罚项的逻辑回归作为基模型的特征选择
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)

  实际上，L1惩罚项降维的原理在于保留多个对目标值具有同等相关性的特征中的一个，所以没选到的特征不代表不重要。故，可结合L2惩罚项来优化。具体操作为：若一个特征在L1中的权值为1，选择在L2中权值差别不大且在L1中权值为0的特征构成同类集合，将这一集合中的特征平分L1中的权值，故需要构建一个新的逻辑回归模型：

from sklearn.linear_model import LogisticRegression

class LR(LogisticRegression):
    def __init__(self, threshold=0.01, dual=False, tol=1e-4, C=1.0,
                 fit_intercept=True, intercept_scaling=1, class_weight=None,
                 random_state=None, solver='liblinear', max_iter=100,
                 multi_class='ovr', verbose=0, warm_start=False, n_jobs=1):

        #权值相近的阈值
        self.threshold = threshold
        LogisticRegression.__init__(self, penalty='l1', dual=dual, tol=tol, C=C,
                 fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight=class_weight,
                 random_state=random_state, solver=solver, max_iter=max_iter,
                 multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs)
        #使用同样的参数创建L2逻辑回归
        self.l2 = LogisticRegression(penalty='l2', dual=dual, tol=tol, C=C, fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight = class_weight, random_state=random_state, solver=solver, max_iter=max_iter, multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs)

    def fit(self, X, y, sample_weight=None):
        #训练L1逻辑回归
        super(LR, self).fit(X, y, sample_weight=sample_weight)
        self.coef_old_ = self.coef_.copy()
        #训练L2逻辑回归
        self.l2.fit(X, y, sample_weight=sample_weight)

        cntOfRow, cntOfCol = self.coef_.shape
        #权值系数矩阵的行数对应目标值的种类数目
        for i in range(cntOfRow):
            for j in range(cntOfCol):
                coef = self.coef_[i][j]
                #L1逻辑回归的权值系数不为0
                if coef != 0:
                    idx = [j]
                    #对应在L2逻辑回归中的权值系数
                    coef1 = self.l2.coef_[i][j]
                    for k in range(cntOfCol):
                        coef2 = self.l2.coef_[i][k]
                        #在L2逻辑回归中，权值系数之差小于设定的阈值，且在L1中对应的权值为0
                        if abs(coef1-coef2) < self.threshold and j != k and self.coef_[i][k] == 0:
                            idx.append(k)
                    #计算这一类特征的权值系数均值
                    mean = coef / len(idx)
                    self.coef_[i][idx] = mean
        return self

  使用feature_selection库的SelectFromModel类结合带L1以及L2惩罚项的逻辑回归模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
 
#带L1和L2惩罚项的逻辑回归作为基模型的特征选择
#参数threshold为权值系数之差的阈值
SelectFromModel(LR(threshold=0.5, C=0.1)).fit_transform(iris.data, iris.target)

3.7 基于树模型的特征选择法(Embedded)

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier

#GBDT作为基模型的特征选择
SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)

作者：城东
链接：https://www.zhihu.com/question/29316149/answer/110159647
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

四、维度压缩

  特征选择完成后，可以直接训练模型，但可能由于特征矩阵过大，导致计算量和计算时间大，因此需要降低矩阵维度。

  主成分分析（PCA）就是最常用的数据降维方法：在减少数据维度的同时，保持对方差贡献最大的特征。

  当特征选择完成后，可以直接训练模型了，但是可能由于特征矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外，另外还有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。

4.1 PCA

  PCA (Principal component analysis，主成分分析)

from sklearn.decomposition import PCA

#主成分分析法，返回降维后的数据
#参数n_components为主成分数目
PCA(n_components=2).fit_transform(iris.data)

4.2 LDA

  LDA （Linear Discriminant Analysis，线性判别分析）

from sklearn.lda import LDA

#线性判别分析法，返回降维后的数据
#参数n_components为降维后的维数
LDA(n_components=2).fit_transform(iris.data, iris.target)

4.3 ICA

  ICA (Independent component analysis，独立成分分析)

在这里插入代码片

'''
【干货来了|小麦苗IT资料分享】
★小麦苗DB职场干货：https://mp.weixin.qq.com/s/Vm5PqNcDcITkOr9cQg6T7w
★小麦苗数据库健康检查：https://share.weiyun.com/5lb2U2M
★小麦苗微店：https://weidian.com/s/793741433?wfr=c&ifr=shopdetail
★各种操作系统下的数据库安装文件（Linux、Windows、AIX等）：链接：https://pan.baidu.com/s/19yJdUQhGz2hTgozb9ATdAw  提取码：4xpv
★小麦苗分享的资料：https://share.weiyun.com/57HUxNi
★小麦苗课堂资料：https://share.weiyun.com/5fAdN5m
★小麦苗课堂试听资料：https://share.weiyun.com/5HnQEuL
★小麦苗出版的相关书籍：https://share.weiyun.com/5sQBQpY
★小麦苗博客文章：https://share.weiyun.com/5ufi4Dx
★数据库系列（Oracle、MySQL、NoSQL）：https://share.weiyun.com/5n1u8gv
★公开课录像文件：https://share.weiyun.com/5yd7ukG
★其它常用软件分享：https://share.weiyun.com/53BlaHX
★其它IT资料（OS、网络、存储等）：https://share.weiyun.com/5Mn6ESi
★Python资料：https://share.weiyun.com/5iuQ2Fn
★已安装配置好的虚拟机：https://share.weiyun.com/5E8pxvT
★小麦苗腾讯课堂：https://lhr.ke.qq.com/
★小麦苗博客：http://blog.itpub.net/26736162/
'''

有趣的事，Python永远不会缺席

欢迎关注小婷儿的博客

  文章内容来源于小婷儿的学习笔记，部分整理自网络，若有侵权或不当之处还请谅解!!!

  如需转发，请注明出处：小婷儿的博客python    https://blog.csdn.net/u010986753

  CSDN https://blog.csdn.net/u010986753

  博客园 https://www.cnblogs.com/xxtalhr/

有问题请在博客下留言或加作者：
  微信：tinghai87605025 联系我加微信群
  QQ ：87605025
  QQ交流群：py_data 483766429
  公众号：DB宝

证书说明

  OCP培训说明连接 https://mp.weixin.qq.com/s/2cymJ4xiBPtTaHu16HkiuA

  OCM培训说明连接 https://mp.weixin.qq.com/s/7-R6Cz8RcJKduVv6YlAxJA

   小婷儿的python正在成长中，其中还有很多不足之处，随着学习和工作的深入，会对以往的博客内容逐步改进和完善哒。重要的事多说几遍。。。。。。