Python时间序列分析--从线性模型到GARCH模型

四级渣渣看个英文文章简直就是自虐，一天只能看一点，还只能看个半懂。唉，写下来以后慢慢理解改正吧。

目录

一、Motivation
二、基础知识
1.平稳性
2.序列相关（自相关）
3.为什么我们关心序列相关性？
三、白噪声和随机游动
四、线性模型
五、对数线性模型
六、AR模型（P）
七、移动平均模型MA（q）
八、自回归滑动平均模型ARMA（p，q）
九、综合自回归移动平均模型ARIMA（p，d，q）
十、自回归条件heterskedastic模型ARCH（p）
十一、广义自回归条件heterskedastic模型GARCH（p，q）

一、Motivation

早期我在做金融方面工作时，我学到了各种时间序列分析的技术和用法，但我不能对怎样将各部分组合到一起有一个更深的理解。我们很难看到为什么我们用某些模型与其他的进行比较或者这些模型如何建立在对方的弱点之上的更大的图景。使用这些技术的根本目的使我困惑了很长时间。直到我理解了这个：

                       **时间序列分析试图明白过去并且预测未来**

通过发展我们的时间序列分析技能，使我们能够更好的明白发生了什么，进而更好的预测未来。示例应用包括预测未来资产回报，未来相关性/协方差和未来波动性。

这篇文章的灵感来自于Michael Halls Moore在他博客上做的伟大工作。我觉得把他的一些工作翻译成Python可以帮助那些对R语言不熟悉的人。我也采用了一些其他博客上的代码。这篇文章是一个活的文件，我可以根据需要和时间流逝的更有用信息来更新他。

Before we begin let’s import our Python libraries.

import os
import sys

import pandas as pd
import pandas_datareader.data as web
import numpy as np

import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
import statsmodels.api as sm
import scipy.stats as scs
from arch import arch_model

import matplotlib.pyplot as plt 
import matplotlib as mpl
%matplotlib inline
p = print

p('Machine:{} {}\n'.format(os.uname().sysname,os.uname().machine))
p(sys.version)

Let’s use the pandas_datareader package to grab some sample data using the Yahoo Finance API.

start = '2010-01-01'
end = '2017-02-25'
get_px = lambda x: web.get_data_yahoo(x, start=start, end=end)['Adj Close']

symbols = ['SPY', 'TLT', 'MSFT']

data = pd.DataFrame({sym:get_px(sym) for sym in symbols})

Irets = np.log(data/data.shift(1)).dropna()

二、基础知识

What is a Time Series? A time series is a series of data points indexed (or listed or graphed) in time order. - Wikipedia
1.平稳性
对数据来说什么是平稳性：
a.序列的平均值不应该是时间的函数。下图中红色的线是不平稳的，因为它的平均值随时间增长。

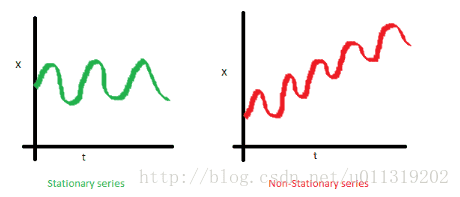
b.序列的方差不应该是时间的函数。这个属性被称为同方差。注意到红色数据随时间的变化很大。

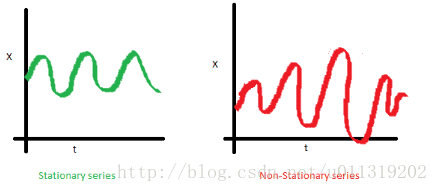
c.最后，第i项和第i+m项的协方差不应该是时间的函数。在下面的图中，你会注意到随时间的推移差距变得越来越近。因此，红色序列的协方差是随时间变化的。

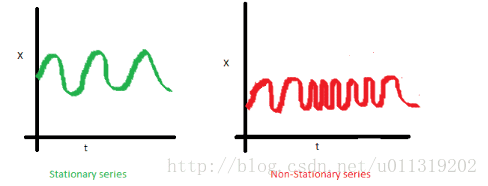
So what? Why do we care about stationarity?

• 一个平稳的时间序列是容易进行预测的，我们可以假设其未来与现在的统计属性是相同的或成比例的。
• 我们用的大多数时间序列分析模型都是假设协方差平稳。这就意味着这些预测模型的统计描述如均值、方差、协方差等只有在序列平稳时才是有效的，否则无效。

如上所说，金融中的大多数时间序列都是不平稳的。因此，有一大部分时间序列分析需要检验我们要预测的序列是否是平定的，如果它不是，我们怎需要找到方法去把它转化成平稳的序列。

2.序列相关（自相关）–Serial Correlation (Autocorrelation)
实质上，当我们对一个时间序列建模时，我们将该系列分成三个部分：趋势、周期和随机。随机分量称为残差或误差。它仅仅是预测值与观测值的差异。当我们模型的残差彼此相关时是自相关。

3.为什么我们关心序列相关性？–Why Do We Care about Serial Correlation?
我们关心的序列相关（自相关）是因为它对我们的模型预测的有效性是至关重要的，是与平稳性密切相关。回想一下，根据定义一个平稳的时间序列的残差是连续不相关的。如果在模型中我们不能解释这一点，我们系数的标准误差的作用会被降低，从而膨胀了T统计量的大小。（If we fail to account for this in our models the standard errors of our coefficients are underestimated, inflating the size of our T-statistics. ）使得结果中存在太多Type-1误差，使得我们拒绝我们的零假设即使是在它是真的。在外行人的术语中，忽略自相关意味着我们的模型预测将是废话，我们在的模型中可能得出了有关自变量的影响的不正确的结论。

三、白噪声和随机游动–White Noise and Random Walks

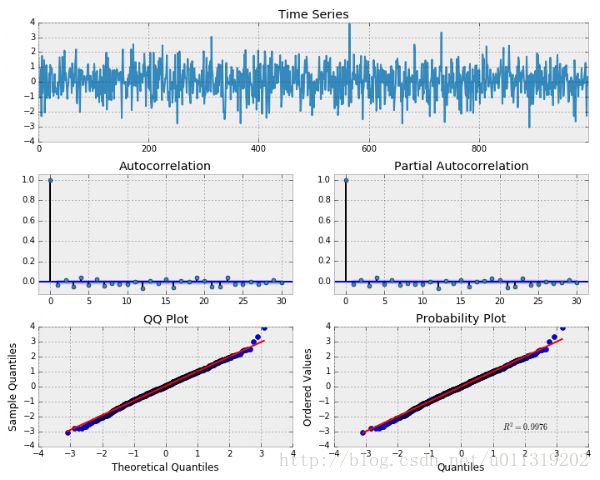
白噪声是第一个我们需要明白的时间序列模型。根据定义，一个白噪声过程的时间序列具有连续不相关的误差，并且那些误差的预期平均值等于零。另一个关于连续不相关误差的描述是独立同分布。这很重要，因为如果我们的TSM是得当的，并且成功的捕获了基本过程，那么我们模型的残差将会是独立同分布的，类似于白噪声过程。因此，一部分时间序列分析是在试图拟合时间序列致使残差序列与白噪声不可区分。

让我们模拟白噪声的过程，并查看它。下面我介绍一个方便的函数，用于绘制时间序列和分析序列相关。

def tsplot(y, lags=None, figsize=(10,8), style='bmh'):
    if not isinstance(y, pd.Series):
        y = pd.Series(y)
    with plt.style.context(style):#定义局部样式
        fig = plt.figure(figsize=figsize)
        layout = (3, 2)
        ts_ax = plt.subplot2grid(layout, (0, 0), colspan=2)
        acf_ax = plt.subplot2grid(layout, (1,0))
        pacf_ax = plt.subplot2grid(layout, (1,1))
        qq_ax = plt.subplot2grid(layout, (2,0))
        pp_ax = plt.subplot2grid(layout, (2,1))

        y.plot(ax=ts_ax)
        ts_ax.set_title('Time Series Analysis Plots')
        smt.graphics.plot_acf(y, lags=lags, ax=acf_ax, alpha=0.5)#自相关系数ACF图
        smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax, alpha=0.5)#偏相关系数PACF图
        sm.qqplot(y, line='s', ax=qq_ax)#QQ图检验是否是正太分布
        qq_ax.set_title('QQ Plot')
        scs.probplot(y, sparams=(y.mean(), y.std()), plot=pp_ax)

        plt.tight_layout()
    return

We can model a white noise process easily and output the TS plot for visual inspection.

np.random.seed(1)
randser = np.random.normal(size=1000)#高斯概率分布
tsplot(randser, lags=30)

我们可以看出这个过程是随机的并且中心为0.ACF和PACF图也显示没有明显的相关性。Keep in mind we should see approximately 5% significance in the autocorrelation plots due to pure chance as a result of sampling from the Normal distribution. 下面我们可以看到QQ和概率图，它将我们数据的分布与另一个理论分布进行比较。在这个示例中，理论分布是标准正态分布。显然，我们的数据是随机分布的，似乎遵循高斯（正常）白噪声，正如它应该是的那样。

p("Random Series\n------------\nmean: {:.3f}\nvariance: {:.3f}\nstandard deviation: {:.3f}"
  .format(randser.mean(), randser.var(), randser.std()))
# Random Series
# -------------
# mean: 0.039 
# variance: 0.962
# standard deviation: 0.981

A Random Walk is defined below:

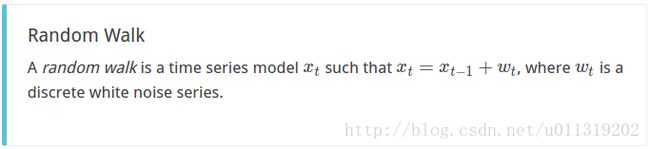
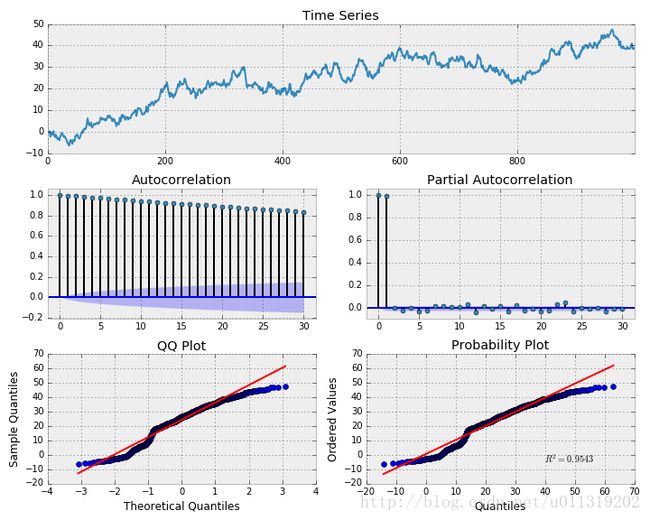
随机游走的意义在于它是非稳定的，因为观察点之间的协方差是时间相关的。如果我们建模的TS是一个随机游走，那么它是不可预测的。
让我们使用“numpy.random.normal（size = our_sample_size）”函数从标准正态分布中抽样模拟一个随机游走。

#Random Walk without a drift
np.random.seed(1)
n_samples = 1000

x = w =np.random.normal(size=n_samples)
for t in range(n_samples):
    x[t] = x[t-1] + w[t]
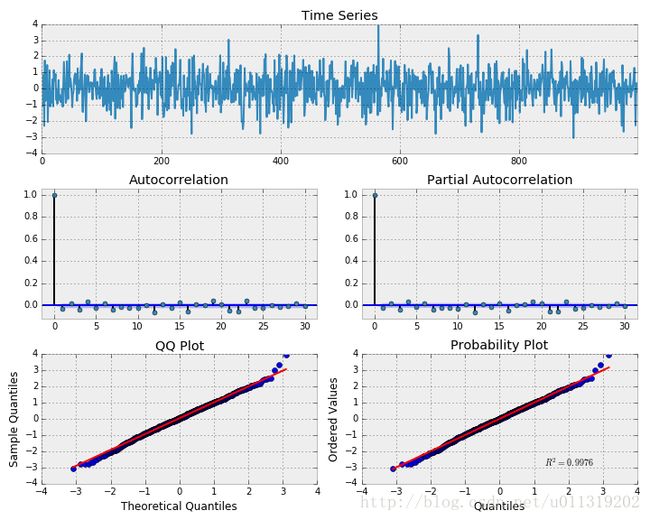
_ = tsplot(x, lags=30)

显然，我们的TS不是固定的。 让我们来看看随机游走模型是否适合我们的模拟数据。 回想一下随机游走是xt = xt-1 + wt。 使用代数我们可以说xt - xt-1 = wt。 因此，我们的随机游走系列的一阶差分应该等于一个白噪声过程！ 我们可以在我们的TS上使用“np.diff（）”函数，看看这是否成立。

#First difference of simulated Random Walk series
#随机游走序列的一阶差分
_ = tsplot(np.diff(x),lags=30)

Our definition holds as this looks exactly like a white noise process. What if we fit a random

walk to the first difference of SPY's prices?
#First difference of SPYprices
#SPY价格的一阶差分
_ = tsplot(np.diff(data.SPY), lags=30 )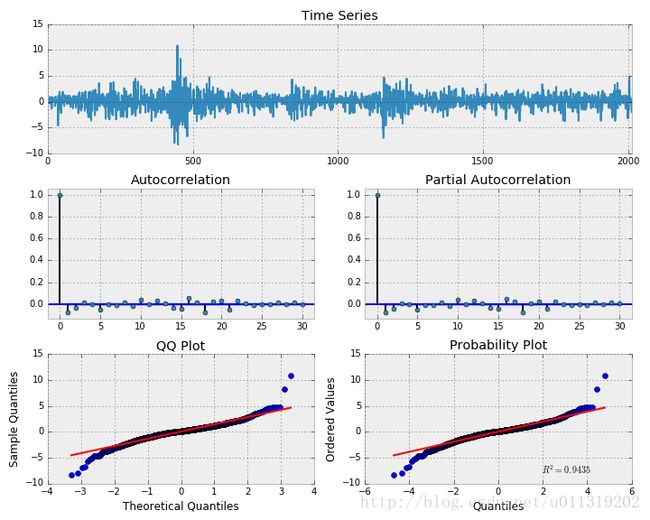

这和白噪声很相似。不过，注意QQ的形状和概率图。这表明，该过程是接近正常，但“重尾”。在ACF和PACF图中似乎也有一些显著的序列相关性，如1，5，16，18，21等。这意味着应该有更好的模型来描述实际的价格变化过程。
注：“重尾”还是不太懂，以后再慢慢看。