深度学习之卷积神经网络
卷积网络介绍
卷积神经网络是一种多层神经网络,擅长处理图像特别是大图像的相关机器学习问题。
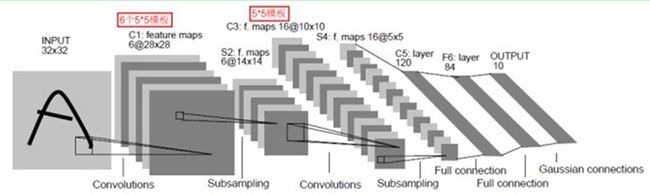
卷积网络通过一系列方法,成功将数据量庞大的图像识别问题不断降维,最终使其能够被训练。CNN最早由Yann LeCun提出并应用在手写字体识别上(MINST)。LeCun提出的网络称为LeNet,其网络结构如下:
这是一个最典型的卷积网络,由卷积层、池化层、全连接层组成。其中卷积层与池化层配合,组成多个卷积组,逐层提取特征,最终通过若干个全连接层完成分类。
卷积层完成的操作,可以认为是受局部感受野概念的启发,而池化层,主要是为了降低数据维度。
综合起来说,CNN通过卷积来模拟特征区分,并且通过卷积的权值共享及池化,来降低网络参数的数量级,最后通过传统神经网络完成分类等任务。
降低参数量级
为什么要降低参数量级?从下面的例子就可以很容易理解了。
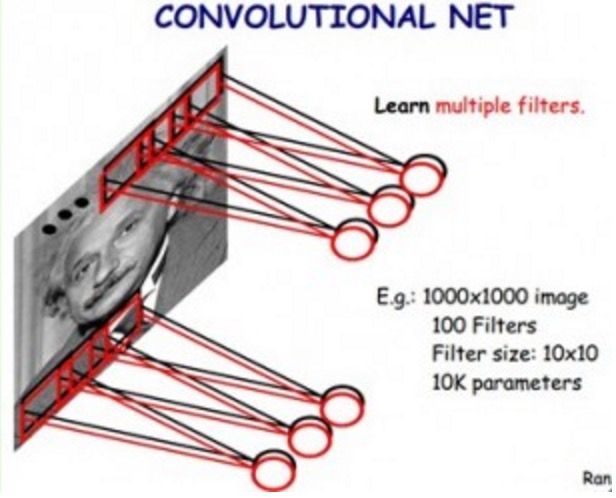
如果我们使用传统神经网络方式,对一张图片进行分类,那么,我们把图片的每个像素都连接到隐藏层节点上,那么对于一张1000x1000像素的图片,如果我们有1M隐藏层单元,那么一共有10^12个参数,这显然是不能接受的。(如下图所示)
![]()
但是我们在CNN里,可以大大减少参数个数,我们基于以下两个假设:
1)最底层特征都是局部性的,也就是说,我们用10x10这样大小的过滤器就能表示边缘等底层特征
2)图像上不同小片段,以及不同图像上的小片段的特征是类似的,也就是说,我们能用同样的一组分类器来描述各种各样不同的图像
基于以上两个,假设,我们就能把第一层网络结构简化如下:
我们用100个10x10的小过滤器,就能够描述整幅图片上的底层特征。
卷积(Convolution)
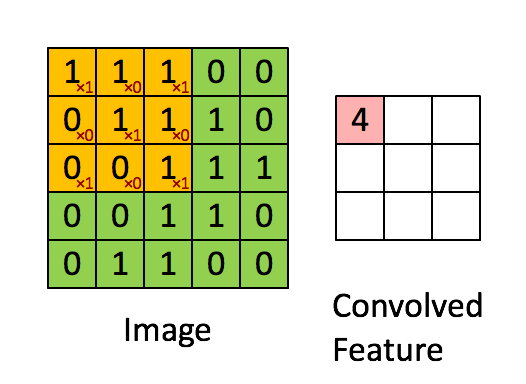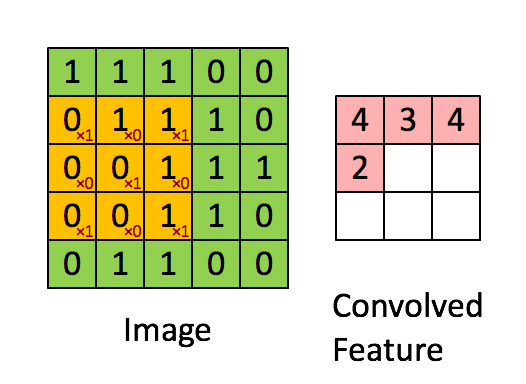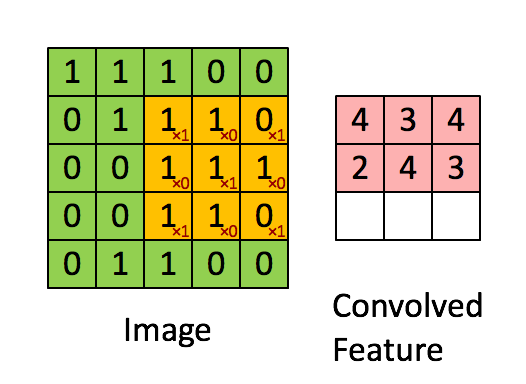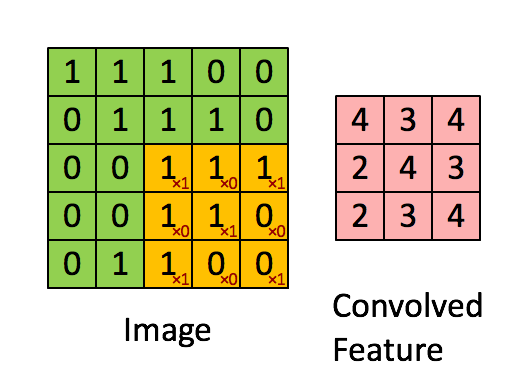
卷积运算的定义如下图所示:
如图所示,我们有一个5x5的图像,我们用一个3x3的卷积核:
1 0 1
0 1 0
1 0 1
来对图像进行卷积操作(可以理解为有一个滑动窗口,把卷积核与对应的图像像素做乘积然后求和),得到了3x3的卷积结果。
这个过程我们可以理解为我们使用一个过滤器(卷积核)来过滤图像的各个小区域,从而得到这些小区域的特征值。
在实际训练过程中,卷积核的值是在学习过程中学到的。
在具体应用中,往往有多个卷积核,可以认为,每个卷积核代表了一种图像模式,如果某个图像块与此卷积核卷积出的值大,则认为此图像块十分接近于此卷积核。如果我们设计了6个卷积核,可以理解:我们认为这个图像上有6种底层纹理模式,也就是我们用6中基础模式就能描绘出一副图像。以下就是24种不同的卷积核的示例:
池化(Pooling)
池化听起来很高深,其实简单的说就是下采样。池化的过程如下图所示:
上图中,我们可以看到,原始图片是20x20的,我们对其进行下采样,采样窗口为10x10,最终将其下采样成为一个2x2大小的特征图。
之所以这么做的原因,是因为即使做完了卷积,图像仍然很大(因为卷积核比较小),所以为了降低数据维度,就进行下采样。
之所以能这么做,是因为即使减少了许多数据,特征的统计属性仍能够描述图像,而且由于降低了数据维度,有效地避免了过拟合。
在实际应用中,池化根据下采样的方法,分为最大值下采样(Max-Pooling)与平均值下采样(Mean-Pooling)。
LeNet介绍
下面再回到LeNet网络结构:
这回我们就比较好理解了,原始图像进来以后,先进入一个卷积层C1,由6个5x5的卷积核组成,卷积出28x28的图像,然后下采样到14x14(S2)。
接下来,再进一个卷积层C3,由16个5x5的卷积核组成,之后再下采样到5x5(S4)。
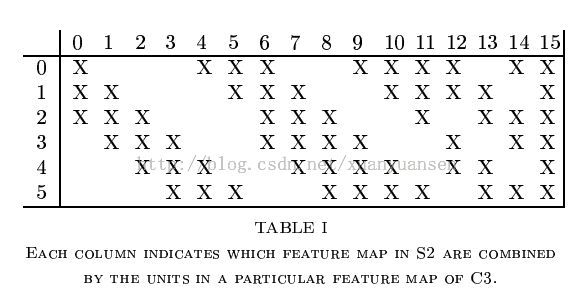
注意,这里S2与C3的连接方式并不是全连接,而是部分连接,如下图所示:
其中行代表S2层的某个节点,列代表C3层的某个节点。
我们可以看出,C3-0跟S2-0,1,2连接,C3-1跟S2-1,2,3连接,后面依次类推,仔细观察可以发现,其实就是排列组合:
0 0 0 1 1 1
0 0 1 1 1 0
0 1 1 1 0 0
...
1 1 1 1 1 1
我们可以领悟作者的意图,即用不同特征的底层组合,可以得到进一步的高级特征,例如:/ + \ = ^ (比较抽象O(∩_∩)O~),再比如好多个斜线段连成一个圆等等。
最后,通过全连接层C5、F6得到10个输出,对应10个数字的概率。
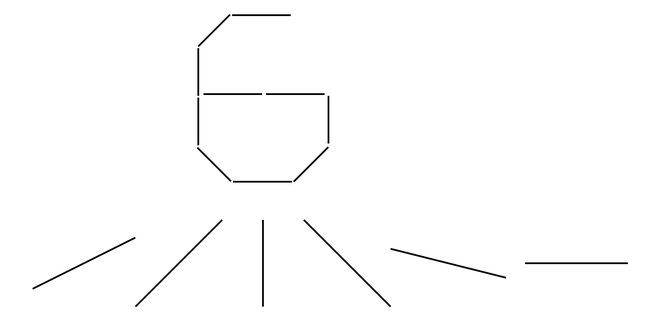
最后说一点个人的想法哈,我认为第一个卷积层选6个卷积核是有原因的,大概也许可能是因为0~9其实能用以下6个边缘来代表:
是不是有点道理呢,哈哈
然后C3层的数量选择上面也说了,是从选3个开始的排列组合,所以也是可以理解的。
其实这些都是针对特定问题的trick,现在更加通用的网络的结构都会复杂得多,至于这些网络的参数如何选择,那就需要我们好好学习了。
训练过程
卷积神经网络的训练过程与传统神经网络类似,也是参照了反向传播算法。
第一阶段,向前传播阶段:
a)从样本集中取一个样本(X,Yp),将X输入网络;
b)计算相应的实际输出Op。
在此阶段,信息从输入层经过逐级的变换,传送到输出层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中,网络执行的是计算(实际上就是输入与每层的权值矩阵相点乘,得到最后的输出结果):
Op=Fn(…(F2(F1(XpW(1))W(2))…)W(n))
第二阶段,向后传播阶段
a)算实际输出Op与相应的理想输出Yp的差;
b)按极小化误差的方法反向传播调整权矩阵。