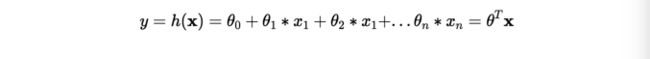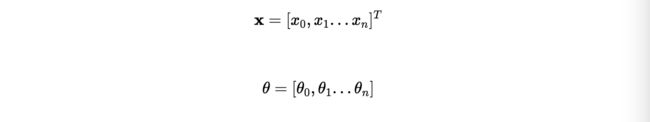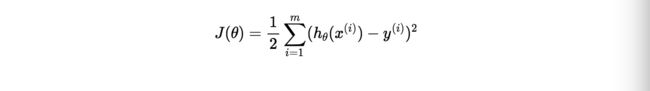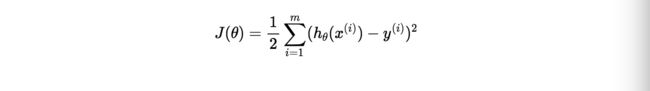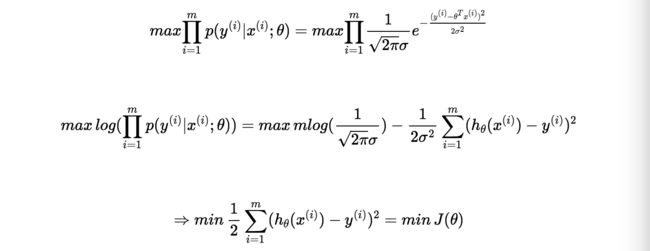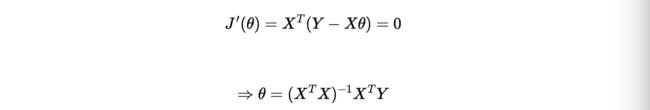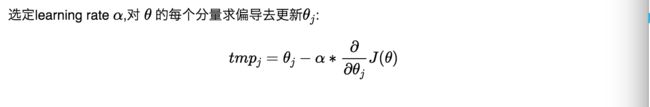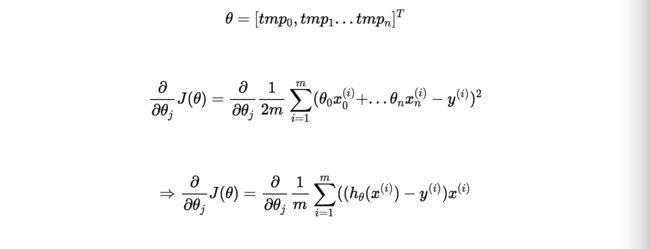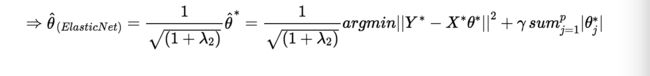回归能做什么呢?《机器学习实战》的作者认为:
回归能做任何事情。
回归模型大致分为2个阶段,训练阶段和预测阶段, 训练阶段需要对历史确定结果的数据进行反馈训练,使得模型的参数适应当前的输入与预期输出, 预测阶段在完善模型的基础上对新的数据进行模拟输出。这两个阶段对于一个模型都至关重要。
回归模型广泛地应用于机器学习,深度学习,AI,人工智能等领域,在这里我们讲对它的应用进行深入浅出的学习与探讨。
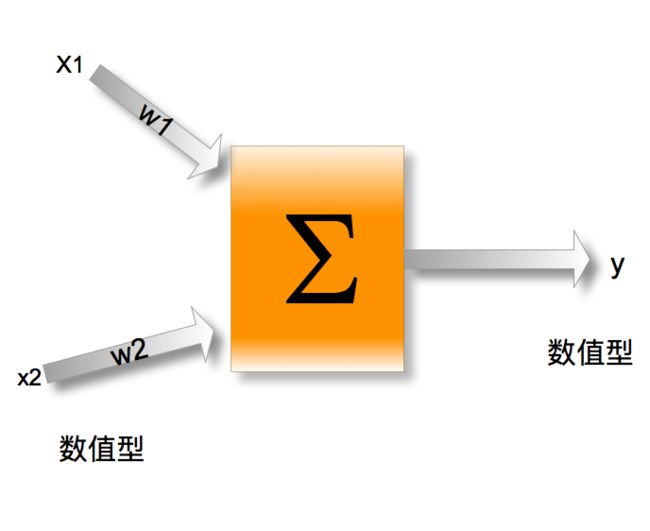
针对不同的数据(数值型和标称型),我们一般有两种预测倾向,数值预测,类别预测,这两种预测有某种潜在的关系,可以说,分类是高层次及符合条件下的数量预测,它建立在数量预测的基础上(这个后面的章节会cover到)
这篇文章的研究环境,基于jupiter notebook, 依赖的python包有pydataset, scilearn, pandas, seaborn以及必要的线性代数,统计学及高等数学的知识, 中无法解析mathjax,所以公式均以截图的形势给出.
线性回归模型
这是最简单的回归模型,也是最general的机器学习算法,也包含了机器学习与回归模型最朴素和使用的思考方法, 它基于一个朴素的假设:输入和输出之间存在简单的线性关系.
其中y 是输出的数值,xi 是输入的数值,x0 =1, n是输入的特征数量
线性回归算法需要确定θ(j)使得平方误差的和最小, 构造损失函数:
这里简单地给出选用误差函数为平方和的概率证明
首先我们提出了一个符合常理的假设:误差是服从均值为0,的高斯分布 的
即
最大似然估计
最小二乘法
对θ求导得到:
梯度下降法
其中
对于n=1时,y=mx+b, python梯度下降代码如下:
def stepGradient(b_current, m_current, points, learningRate):
b_gradient = 0
m_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
b_gradient += -(2/N) * (points[i].y - ((m_current*points[i].x) + b_current))
m_gradient += -(2/N) * points[i].x * (points[i].y - ((m_current * points[i].x) + b_current))
new_b = b_current - (learningRate * b_gradient)
new_m = m_current - (learningRate * m_gradient)
return [new_b, new_m]
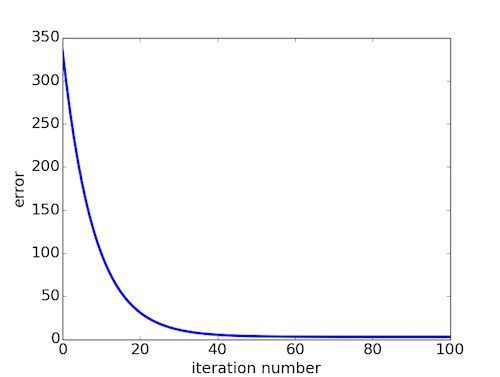
重复执行stepGradient后得到J(θ)与执行次数的关系:
下面是sklearn的线性模型的应用:
from sklearn import datasets
from sklearn.cross_validation import cross_val_predict
from sklearn import linear_model
import matplotlib.pyplot as plt
lr = linear_model.LinearRegression()
boston = datasets.load_boston()
y = boston.target
# cross_val_predict returns an array of the same size as `y` where each entry
# is a prediction obtained by cross validated:
predicted = cross_val_predict(lr, boston.data, y, cv=10)
fig, ax = plt.subplots()
ax.scatter(y, predicted)
ax.plot([y.min(), y.max()], [y.min(), y.max()], 'k--', lw=4)
ax.set_xlabel('Measured')
ax.set_ylabel('Predicted')
plt.show()
回归的正则化与特征选择
为了避免过拟合的问题,使模型更general一些,正则化的理念被提了出来,正则化被用来减小单个θ(j)的影响,基本原理是在全局损失函数中加入惩罚函数
Elastic net方法
这便转化为了普通的套索问题
参考:
似然函数
最小二乘法
矩阵,向量求导
极大似然估计
广义线性模型基于Elastic+Net的变量选择方法研究