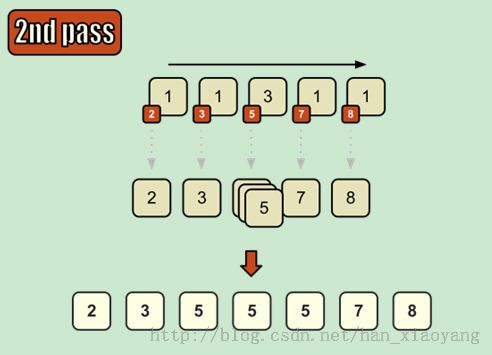GIF演示排序算法
最近在准备笔试,面试,看了不少关于排序算法的知识,总感觉代码有余,直观不足。
所以想利用直观的GIF动图来演示各种排序算法。
1.插入排序(Insertion Sort)
1.1算法简介
插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
1.2GIF动态图演示
1.3时间复杂度与空间复杂度分析
时间复杂度:O(n^2)
空间复杂度:O(1)
最少比较次数:(已排序的数组)n-1次
最多比较次数:(降序的数组)n(n-1)/2次
赋值操作次数:比较次数-(n-1)
插入排序不适合对大量数据排序,适合对接近排序的数据排序。
插入排序是稳定排序。
1.4 插入排序的STL源码
阅读源码总是让人受益匪浅,STL实现各种数据结构与算法的方法之巧妙,考虑之全面,我一直十分佩服,这里贴出STL源码中实现InsertSort的方法。
SGI STL中的InsertSort有两个版本,版本一以递增的方式排序,版本二允许指定仿函数,作为元素的比较函数,下面仅介绍版本一。
//STL并不开放Insertion Sort,用双下划线表示内部使用
template <class RandomAccessIterator>
void __insertion_sort(RandomAccessIterator first,
RandomAccessIterator last)
{
if ( first == last ) return;
for(RandomAccessIterator i = first + 1; i != last; i++) //外循环,i递增
{
//内循环,辅助函数
__linear_insert(first, i, value_type(first));
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
内循环辅助函数linear_insert
//__linear_insert
template
inline void __linear_insert(RandomAccessIterator first,
RandomAccessIterator last,T*)
{
T value=*last; //记录尾元素
if (value < *first)
{
//如果尾元素比头元素还要小
//没必要在一个个比较了,直接将整个区间右移一个位置
copy_backward(first, last, last + 1);
*first = value;
}
else
{
//正常的比较逻辑
__unguarded_linear_insert(last,value);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
辅助函数
template
void __unguarded_linear_insert(RandomAccessIterator last, T value)
{
RandomAccessIterator next=last;
--next;
while(value < *next)
{
*last = *next;
last=next;
--next;
}
*last = value;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
2.快速排序(Quick Sort)
2.1算法简介
快速排序是由东尼·霍尔所发展的一种排序算法。其基本思想是基本思想是,通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
2.2GIF动态图演示
2.3时间复杂度与空间复杂度
最差时间复杂度:O(N^2)
最优时间复杂度:O(NlogN)
平均时间复杂度:O(NlogN)
空间复杂度:与具体的实现策略有关
2.4快速排序的STL源码实现
在SGI STL中使用introsort代替median-of-three quicksort,其实两者十分接近,但是introsort在最差情况下,时间复杂度仍然保持为O(NlogN)
这里介绍median-of-three quicksort。

分割Partitioning
//Paritioning
template <class T>
inline const T& __median(const T& a,const T& b,const T& c)
{
if(aif(breturn b;
else if(a//a=c,a
return c;
else //a=c,a>=c
return a;
}
else if (areturn a;
else if (b//a>=b,a>=c,b
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
3.二分插入排序
3.1算法简介
二分(折半)插入(Binary insert sort)排序是一种在直接插入排序算法上进行小改动的排序算法。其与直接排序算法最大的区别在于查找插入位置时使用的是二分查找的方式,在速度上有一定提升。
但是,在查找二分点的时间上的时间损耗,导致了这个算法并不能比直接插入排序优秀多少,除非你有十分确切的数据大小和随机访问迭代器。
3.2时间复杂度与空间复杂度
平均时间复杂度:O(N^2)
最差时间复杂度:O(N^2)
最优时间复杂度:O(NlogN)
空间复杂度:O(1)
3.3GIF动态度演示
4.希尔排序
4.1算法简介
希尔排序,也称递减增量排序算法,因DL.Shell于1959年提出而得名,是最早突破二次时间屏障的排序算法,是插入排序的一种高速而稳定的改进版本。
希尔排序的时间复杂度与增量选取有关,至今未能给出算法的时间复杂度的下界
4.2时间复杂度与空间复杂度
最差时间复杂度:O(N^2)
空间复杂度:O(1)
4.3GIF动态图演示
5.选择排序
5.1算法简介
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
5.2时间复杂度与空间复杂度
时间复杂度:O(N^2)
空间复杂度:O(1)
5.3GIF动态图演示
6.冒泡排序
6.1算法简介
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
6.2时间复杂度与空间复杂度
最差时间复杂度:O(N^2)
最优时间复杂度:O(N)
平均时间复杂度:O(N^2)
空间复杂度:O(1)
6.3GIF动态图演示
7双向冒泡排序/鸡尾酒排序
7.1算法简介
鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。
7.2时间复杂度与空间复杂度
最差时间复杂度:O(N^2)
最优时间复杂度:O(N)
平均时间复杂度:O(N^2)
空间复杂度:O(1)
7.3GIF动态图演示
8堆排序
8.1算法简介
不得不说,堆排序太容易出现了,选择填空问答算法大题都会出现。建堆的过程,堆调整的过程,这些过程的时间复杂度,空间复杂度,以及如何应用在海量数据Top K问题中等等,都是需要重点掌握的。
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
8.2时间复杂度与空间复杂度
最差时间复杂度:O(NlogN)
最优时间复杂度:O(NlogN)
平均时间复杂度:O(NlogN)
最差空间复杂度:O(n)
最优空间复杂度:O(1)
8.3GIF动态图演示
9归并排序
9.1算法简介
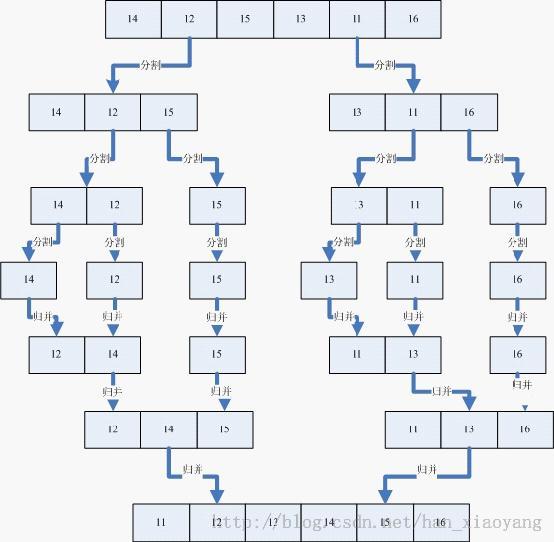
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
9.2时间复杂度与空间复杂度
最差时间复杂度:O(NlogN)
最优时间复杂度:O(NlogN)
平均时间复杂度:O(NlogN)
空间复杂度:O(n)
9.3图解
10桶排序
10.1算法简介
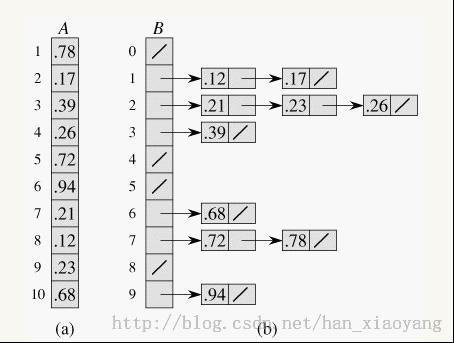
桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。
桶排序是稳定的,且在大多数情况下常见排序里最快的一种,比快排还要快,缺点是非常耗空间,基本上是最耗空间的一种排序算法,而且只能在某些情形下使用。
10.2时间复杂度与空间复杂度
时间复杂度:O(N)
最优空间复杂度:O(N)
10.3图解
11计数排序
11.1算法简介
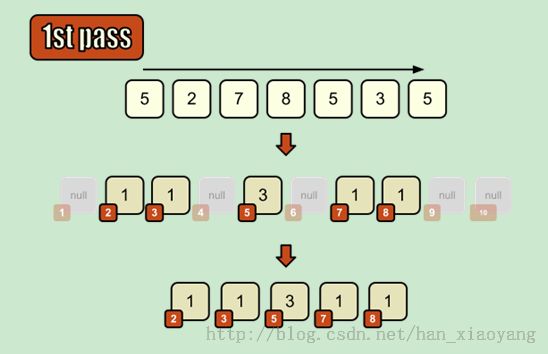
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
11.2时间复杂度与空间复杂度
时间复杂度:O(N)
空间复杂度:取决于计数范围
11.3图解
12基数排序
12.1算法简介
基数排序是一种非比较型整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数,所以基数排序也不是只能使用于整数。基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机(Tabulation Machine)上的贡献。
12.2时间复杂度与空间复杂度
时间复杂度:O(NlogN)