数据分析系列：生存分析（生存曲线分析、Cox回归分析）——附生存分析python代码。

上一篇文章写了数据分析系列：归因分析原理、案例和python代码。但是现实中用户所归属的渠道可能很多，比如用户在网上商城的首页点击了一个产品，又在其他公众号的相关推荐点击了此产品，在所有转化用户中，每个渠道的贡献率是多大？这就是归因分析中的多渠道归因。

对于多渠道归因，有一些启发式的归因方法，比如“最终点击”（将订单归属于最后一个渠道）、“非最终点击”（归属于倒数第二个渠道）、“首次点击”（第一次点击）、“线性衰减”（时间越远权重越小）、“线性平均”（各经历渠道权重相同）、“根据位置”（自己定义每个位置权重），可参考Google Analysis

上面的启发式归因，需要人为定义渠道归属或每个位置的权重，在大多数情况，当合理根据业务定义归属时，得出的结果是合理的，也是使用最多的方法。但是却避免不了存在主观性的缺点。**还有一个是根据算法归因的方式，包括使用逻辑回归、生存分析中的cox回归，马尔科夫链等。

其中逻辑回归和生存分析的多渠道归因大致方法是，求出回归中对应每个渠道前的系数${\beta }_i$，再根据${\beta }_i$求出对应的odd ratios：$exp({\beta }_i)$（cox回归可以直接求出RR），再根据前一篇数据分析系列：归因分析原理、案例和python代码相关的公式求出每个渠道的PAF。

马尔科夫链的大致计算方式是：计算每个渠道之间以及最初/终状态（start、转化、未转化）之间的状态转移概率矩阵，再每次去掉其中一个渠道，计算其移除效应，再对每个渠道的移除效应进行标准化，最终的得到就是这个渠道的贡献大小。

逻辑回归不用多说了，到处都在用。网上的生存分析大多是使用R或者SPSS。本文主要使用python进行生存分析。

生存分析的理论很多，本文不涉及，推荐写的很好的生存分析系列文章生存分析简介。写的非常清晰，本人也是在长时间不使用后，看着这个系列的文章才慢慢回想起来。

在python中，生存分析的包是lifelines，可以利用lifelines进行累计生存曲线的绘制、Log Rank test、Cox回归等。

一、绘制S(t)

先使用自带的数据集

from lifelines.datasets import load_waltons
from lifelines import KaplanMeierFitter
from lifelines.utils import median_survival_times

df = load_waltons()
print(df.head(),'\n')
print(df['T'].min(), df['T'].max(),'\n')
print(df['E'].value_counts(),'\n')
print(df['group'].value_counts(),'\n')

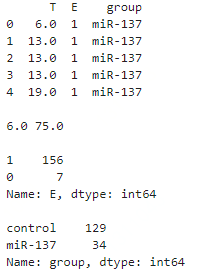
可以看到数据有三列，其中T代表min(T, C)，其中T为死亡时间，C为观测截止时间。E代表是否观察到“死亡”，1代表观测到了，0代表未观测到，即生存分析中的删失数据，共7个。 group代表是否存在病毒， miR-137代表存在病毒，control代表为不存在即对照组，根据统计，存在miR-137病毒人数34人，不存在129人。

利用此数据取拟合拟生存分析中的Kaplan Meier模型（专用于估计生存函数的模型），并绘制全体人群的生存曲线。

kmf = KaplanMeierFitter()
kmf.fit(df['T'], event_observed=df['E'])

kmf.plot_survival_function()

median_ = kmf.median_survival_time_
median_confidence_interval_ = median_survival_times(kmf.confidence_interval_)
print(median_confidence_interval_)

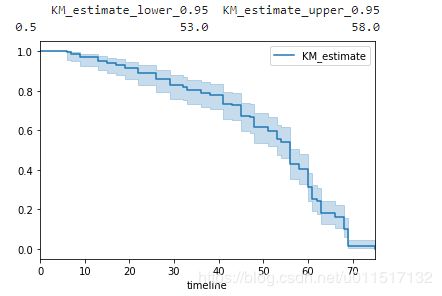
图中蓝色实线为生存曲线，浅蓝色带代表了95%置信区间。随着时间增加，存活概率S(t)越来越小，这是一定的，同时S(t)=0.5时，t的95%置信区间为[53, 58]。这并不是我们关注的重点，我们真正要关注的实验组（存在病毒）和对照组（未存在病毒）的生存曲线差异。因此我们要按照group等于“miR-137”和“control”分组，分别观察对应的生存曲线:

groups = df['group']
ix = (groups == 'miR-137')

kmf.fit(df['T'][ix], df['E'][ix], label='miR-137')
ax = kmf.plot()
treatment_median_confidence_interval_ = median_survival_times(kmf.confidence_interval_)
print("带有miR-137病毒存活50%对应的存活时间95%置信区间：'\n'", treatment_median_confidence_interval_, '\n')

kmf.fit(df['T'][~ix], df['E'][~ix], label='control')
#共享一个画布
ax = kmf.plot(ax=ax)

control_median_confidence_interval_ = median_survival_times(kmf.confidence_interval_)
print("未带有miR-137病毒存活50%对应的存活时间95%置信区间：'\n'", control_median_confidence_interval_)

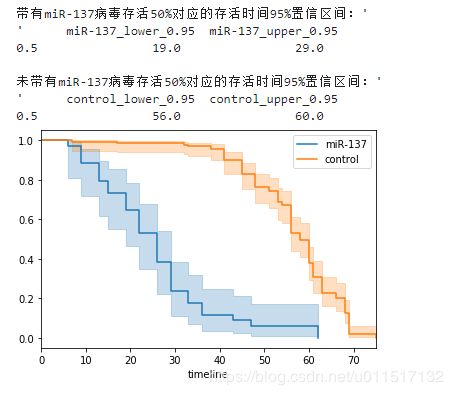
可以看到，带有miR-137病毒的生存曲线在control组下方。说明其平均存活时间明显小于control组。同时带有miR-137病毒存活50%对应的存活时间95%置信区间为[19,29]，对应的control组为[56,60]。差异较大，这个方法可以应用在分析用户流失等场景，比如我们对一组人群实行了一些防止流行活动，我们可以通过此种方式分析我们活动是否有效。

二、Cox回归

通常存活时间与多种因素都存在关联，因此我们的面临的数据是多维的。下面使用一个更复杂的数据集。

from lifelines.datasets import load_regression_dataset
from lifelines import CoxPHFitter

regression_dataset = load_regression_dataset()

print(regression_dataset.head())
print(regression_dataset['E'].value_counts())

其中T代表min(T, C)，其中T为死亡时间，C为观测截止时间。E代表是否观察到“死亡”，1代表观测到了，0代表未观测到，即生存分析中的**“删失”**数据，删失数据共11个。var1,var2,var3代表了我们关系的变量，可以是是否为实验组的虚拟变量，可以是一个用户的渠道路径，也可以是用户自身的属性

我们利用此数据进行Cox回归

cph = CoxPHFitter()
cph.fit(regression_dataset, 'T', event_col='E')
cph.print_summary()

结果分析：从结果来看，我们认为var1和var3在5%的显著性水平下是显著的。认为var1水平越高，用户的风险函数值越大，即存活时间越短（cox回归是对风险函数建模，这与死亡加速模型刚好相反，死亡加速模型是对存活时间建模，两个模型的参数符号相反）。同理，var3水平越高，用户的风险函数值越大。

我们看到结果中第二列为exp(coef)，我们还可以利用这个数字代替RR值，带入PAF的计算公式进行归因分析。请参考我的另一篇博客数据分析系列：归因分析原理、案例和python代码