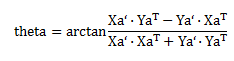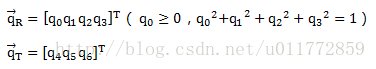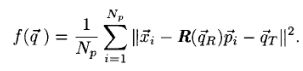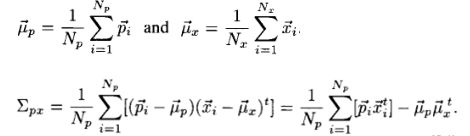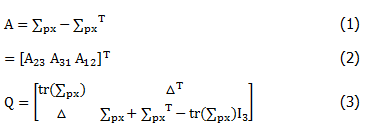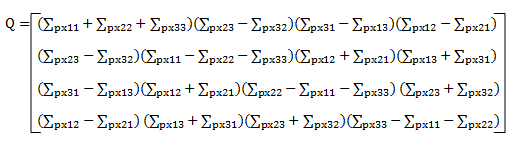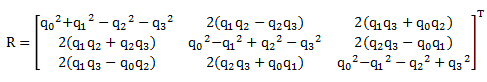迭代最邻近匹配算法(icp)及三维人脸匹配实例

不好意思，太久没上没有回复各位。这个小实验的demo已上传至

http://download.csdn.net/download/u011772859/10224072，不包含显示程序。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

概述：3dIcp算法由Paul J.Besl1992年提出。它的基础是对应点集匹配算法。对应点匹配的思想是：通过对点集的旋转、平移使得两点集的误差平方和最小。在两个点集并未一一对应时，icp算法采用“距离最近的点”为标准为库集中每一个点匹配一个对应点。当对象点数很多时，匹配过程的时间代价占据了主导地位。目前各种对icp的改进方法很多是在点集配对上做文章。

2d对应点匹配算法：

点集中的每个元素为二维点（xi，yi），点集A在B上的对应点集为A’，共有N个元素。一次迭代逼近由旋转矩阵、平移矩阵构成，作用在测试集B上Theta是旋转角度，x，y是要平移的量。

[cos(theta)  sin(theta)   x

-sin(theta)   cos(theta)  y

0           0            1]

也可以直接构造二维矩阵R  

[cos(theta)  sin(theta)   

-sin(theta)   cos(theta)]      (1)

A’R=A                             (2)

最小二乘法原则构造目标函数E=sum[(Xa-Xa')^2+(Ya-Ya')^2] (3)

将(1)(2)带入(3)中，得到E(theta)表达式，对theta求导令之为0，可求的theta的表达式：

求得theta后得到旋转矩阵R，旋转后再将两点集的质心平移到一起即可。

3d对应匹配算法

采用四元数向量qR表示旋转，qT表示平移，

完整的匹配向量为

算法过程

1.用最近距离或其他方法从要匹配的两个点集X’，P’中确定对应点集X 和P, X={xi}， P={pi}，i=1,2，…Np

目标函数：

2.对X和P求出去重心化后的互协方差矩阵

3.构建4*4正定阵Q

    

将(1) (2)带入(3)中，得到

4.构建旋转矩阵R

对Q进行特征值分解，取最大特征值对应的特征向量作为qr=[q0q1q2q3]T

构造旋转矩阵R

在对P集R变换后再做重心平移即可。

5计算误差函数，是否达到某一阈值，否则回到1。

matlab代码及关键函数供参考：

datag=load('F:\face1.asc');
datap=load('F:\face2.asc');
datap=rotateup(20,datap);
Write3dData('F:\face3.txt',datap);
[datag,datap1,error] = ICP3d(datag,datap);
err=mean(error(:,1));
lasterror=0;
k=0;
while abs(err-lasterror)>0.01
    k=k+1;
    lasterror=err;
    [datag,datap,error] = ICP3d(datag,datap);
    err=mean(error(:,1));
end                           %icp匹配
Write3dData('F:\1.txt',datag);
Write3dData('F:\2.txt',datap);               

function [datag1,datap1,error] = ICP3d(datag,datap)
%ICP3d datag--Gallery data  datap--Probe data  
%error--mean square error vector
[k1,n]=size(datag);
[k2,m]=size(datap);
data1=zeros(k1,3);%中间点集
datapp=zeros(k1,3);%对应点集
distance=zeros(k1,1);
error=zeros(k1,1);%对应点之间误差点集
for i=1:1:k1
    datap1(:,1)=datap(:,1)-datag(i,1);
    datap1(:,2)=datap(:,2)-datag(i,2);
    datap1(:,3)=datap(:,3)-datag(i,3);
    distance=datap1(:,1).^2+datap1(:,2).^2+datap1(:,3).^2;
    [mi,minindex]=min(distance);
    datapp(i,:)=datap(minindex,:);
    error(i)=mi;
end                %用最近距离找对应点

[datag]=normalGravity(datag);
[datapp]=normalGravity(datapp);%去重心化
V=(datag'*datapp)./k1;%协方差矩阵
 matrix4 = [V(1,1)+V(2,2)+V(3,3),V(2,3)-V(3,2),V(3,1)-V(1,3),V(1,2)-V(2,1);
            V(2,3)-V(3,2),V(1,1)-V(2,2)-V(3,3),V(1,2)+V(2,1),V(1,3)+V(3,1);
            V(3,1)-V(1,3),V(1,2)+V(2,1),V(2,2)-V(1,1)-V(3,3),V(2,3)+V(3,2);
            V(1,2)-V(2,1),V(1,3)+V(3,1),V(2,3)+V(3,2),V(3,3)-V(1,1)-V(2,2)]; 
                    %对称阵
 [V2,D2] =eig(matrix4); 
 a=[D2(1,1),D2(2,2),D2(3,3),D2(4,4)];
[x,n]=max(a);
Q=V2(:,n);  %最大特征值对应的向量
R=[Q(1,1)^2+Q(2,1)^2-Q(3,1)^2-Q(4,1)^2,     2*(Q(2,1)*Q(3,1)-Q(1,1)*Q(4,1)),        2*(Q(2,1)*Q(4,1)+Q(1,1)*Q(3,1));
   2*(Q(2,1)*Q(3,1)+Q(1,1)*Q(4,1)),         Q(1,1)^2-Q(2,1)^2+Q(3,1)^2-Q(4,1)^2,    2*(Q(3,1)*Q(4,1)-Q(1,1)*Q(2,1));
   2*(Q(2,1)*Q(4,1)-Q(1,1)*Q(3,1)),         2*(Q(3,1)*Q(4,1)+Q(1,1)*Q(2,1)),        Q(1,1)^2-Q(2,1)^2-Q(3,1)^2-Q(4,1)^2;
];          %旋转矩阵
datap=datap*R;
[datap1]=normalGravity(datap);%质心移到一起
[datag1]=normalGravity(datag);
end

face1&face3
err=156.1272

1&2

err=1.8852