【Graph Embedding】Struc2Vec：算法原理，实现和应用
本文首发于知乎专栏
https://zhuanlan.zhihu.com/p/56733145
，欢迎关注~
前面介绍过DeepWalk,LINE,Node2Vec,SDNE几个graph embedding方法。这些方法都是基于近邻相似的假设的。其中DeepWalk,Node2Vec通过随机游走在图中采样顶点序列来构造顶点的近邻集合。LINE显式的构造邻接点对和顶点的距离为1的近邻集合。SDNE使用邻接矩阵描述顶点的近邻结构。
事实上，在一些场景中，两个不是近邻的顶点也可能拥有很高的相似性，对于这类相似性，上述方法是无法捕捉到的。Struc2Vec就是针对这类场景提出的。Struc2Vec的论文发表在2017年的KDD会议中。
Struc2Vec算法原理
相似度定义
Struc2Vec是从空间结构相似性的角度定义顶点相似度的。
用下面的图简单解释下，如果在基于近邻相似的模型中，顶点u和顶点v是不相似的，第一他们不直接相连，第二他们不共享任何邻居顶点。
而在struc2vec的假设中，顶点u和顶点v是具有空间结构相似的。他们的度数分别为5和4，分别连接3个和2个三角形结构，通过2个顶点(d,e;x,w)和网络的其他部分相连。
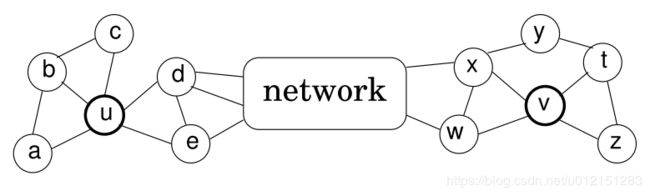直观来看，具有相同度数的顶点是结构相似的，若各自邻接顶点仍然具有相同度数，那么他们的相似度就更高。
顶点对距离定义
令 R k ( u ) R_k(u) Rk(u)表示到顶点u距离为k的顶点集合，则 R 1 ( u ) R_1(u) R1(u)表示是u的直接相连近邻集合。
令 s ( S ) s(S) s(S)表示顶点集合 S S S的有序度序列。
通过比较两个顶点之间距离为k的环路上的有序度序列可以推出一种层次化衡量结构相似度的方法。
令 f k ( u , v ) f_k(u,v) fk(u,v)表示顶点u和v之间距离为k（这里的距离k实际上是指距离小于等于k的节点集合）的环路上的结构距离(注意是距离，不是相似度)。
f k ( u , v ) = f k − 1 ( u , v ) + g ( s ( R k ( u ) ) , s ( R k ( v ) ) ) , k ≥ 0 and ∣ R k ( u ) ∣ , ∣ R k ( v ) ∣ > 0 f_k(u,v)=f_{k-1}(u,v)+g(s(R_k(u)),s(R_k(v))),k\ge 0 \text{ and } |R_k(u)|,|R_k(v)|>0 fk(u,v)=fk−1(u,v)+g(s(Rk(u)),s(Rk(v))),k≥0 and ∣Rk(u)∣,∣Rk(v)∣>0
其中 g ( D 1 , D 2 ) ≥ 0 g(D_1,D_2)\ge 0 g(D1,D2)≥0是衡量有序度序列 D 1 D_1 D1和 D 2 D_2 D2的距离的函数，并且 f − 1 = 0 f_{-1}=0 f−1=0.
下面就是如何定义有序度序列之间的比较函数了，由于 s ( R k ( u ) ) s(R_k(u)) s(Rk(u))和 s ( R k ( v ) ) s(R_k(v)) s(Rk(v))的长度不同，并且可能含有重复元素。所以文章采用了**Dynamic Time Warping(DTW)**来衡量两个有序度序列。
一句话，DTW可以用来衡量两个不同长度且含有重复元素的的序列的距离（距离的定义可以自己设置）。
基于DTW，定义元素之间的距离函数
d ( a , b ) = m a x ( a , b ) m i n ( a , b ) − 1 d(a,b)=\frac{max(a,b)}{min(a,b)}-1 d(a,b)=min(a,b)max(a,b)−1
至于为什么使用这样的距离函数，这个距离函数实际上惩罚了当两个顶点的度数都比较小的时候两者的差异。举例来说，
a = 1 , b = 2 a=1,b=2 a=1,b=2情况下的距离为1， a = 101 , b = 102 a=101,b=102 a=101,b=102情况下的距离差异为0.0099。这个特性正是我们想要的。
构建层次带权图
根据上一节的距离定义，对于每一个 k k k我们都可以计算出两个顶点之间的一个距离，现在要做的是通过上一节得到的顶点之间的有序度序列距离来构建一个层次化的带权图（用于后续的随机游走）。
我们定义在某一层 k k k中两个顶点的边权为 w k ( u , v ) = e − f k ( u , v ) , k = 0 , . . . , k ∗ w_k(u,v)=e^{-f_k(u,v)},k=0,...,k^* wk(u,v)=e−fk(u,v),k=0,...,k∗
这样定义的边权都是小于1的，当且仅当距离为0的是时候，边权为1。
通过有向边将属于不同层次的同一顶点连接起来，具体来说，对每个顶点，都会和其对应的上层顶点还有下层顶点相连。边权定义为
w ( u k , u k + 1 ) = log ( Γ k ( u ) + e ) , k = 0 , . . . , k ∗ − 1 w(u_k,u_{k+1})=\log{(\Gamma_{k}(u)+e)},k=0,...,k^*-1 w(uk,uk+1)=log(Γk(u)+e),k=0,...,k∗−1
w ( u k , u k − 1 ) = 1 , w(u_k,u_{k-1})=1, w(uk,uk−1)=1,
其中 Γ k ( u ) \Gamma_k(u) Γk(u)是第k层与u相连的边的边权大于平均边权的边的数量。
Γ k ( u ) = ∑ v ∈ V 1 ( w k ( u , v ) > w k ˉ ) \Gamma_k(u) = \sum_{v \in V} 1(w_k(u,v)>\bar{w_k}) Γk(u)=∑v∈V1(wk(u,v)>wkˉ)
w k ˉ \bar{w_k} wkˉ就是第k层所有边权的平均值。
采样获取顶点序列
使用有偏随机游走在构造出的图 M M M中进行顶点序列采样。
每次采样时，首先决定是在当前层游走，还是切换到上下层的层游走。
若决定在当前层游走，设当前处于第k层，则从顶点u到顶点v的概率为：
p k ( u , v ) = e − f k ( u , v ) Z k ( u ) p_k(u,v)=\frac{e^{-f_k(u,v)}}{Z_k(u)} pk(u,v)=Zk(u)e−fk(u,v)
其中 Z k ( u ) = ∑ v ∈ V , v ≠ u e − f k ( u , v ) Z_k(u)=\sum_{v\in V,v\ne u}e^{-f_k(u,v)} Zk(u)=∑v∈V,v=ue−fk(u,v)是第k层中关于顶点u的归一化因子。
通过在图M中进行随机游走，每次采样的顶点更倾向于选择与当前顶点结构相似的顶点。因此，采样生成的上下文顶点很可能是结构相似的顶点，这与顶点在图中的位置无关。
若决定切换不同的层，则以如下的概率选择 k + 1 k+1 k+1层或 k − 1 k-1 k−1层，
p k ( u k , u k + 1 ) = w ( u k , u k + 1 ) w ( u k , u k + 1 ) + w ( u k , u k − 1 ) p_k(u_k,u_{k+1})=\frac{w(u_k,u_{k+1})}{w(u_k,u_{k+1})+w(u_k,u_{k-1})} pk(uk,uk+1)=w(uk,uk+1)+w(uk,uk−1)w(uk,uk+1)
p k ( u k , u k − 1 ) = 1 − p k ( u k , u k + 1 ) p_k(u_k,u_{k-1})=1-p_k(u_k,u_k+1) pk(uk,uk−1)=1−pk(uk,uk+1)
三个时空复杂度优化技巧
OPT1 有序度序列长度优化
前面提到过对于每个顶点在每一层都有一个有序度序列，而每一个度序列的空间复杂度为O(n)。
文章提出一种压缩表示方法，对于序列中出现的每一个度，计算该度在序列里出现的次数。压缩后的有序度序列存储的是**(度数，出现次数)**这样的二元组。
同时修改距离函数为：
d i s t ( a , b ) = ( m a x ( a 0 , b 0 ) m i n ( a 0 , b 0 ) − 1 ) m a x ( a 1 , b 1 ) dist(a,b)=(\frac{max(a_0,b_0)}{min(a_0,b_0)}-1)max(a_1,b_1) dist(a,b)=(min(a0,b0)max(a0,b0)−1)max(a1,b1)
a 0 , b 0 a_0,b_0 a0,b0为度数， a 1 , b 1 a_1,b_1 a1,b1为出现次数。
OPT2 相似度计算优化
在原始的方法中，我们需要计算每一层k中，任意两个顶点之间的相似度。事实上，这是不必要的。因为两个度数相差很大的顶点，即使在 k = 0 k=0 k=0的时候他们的距离也已经非常大了，那么在随机游走时这样的边就几乎不可能被采样到，所以我们也没必要计算这两个顶点之间的距离。
文章给出的方法是在计算顶点u和其他顶点之间的距离时，只计算那些与顶点u的度数接近的顶点的距离。具体来说，在顶点u对应的有序度序列中进行二分查找，查找的过程就是不断逼近顶点u的度数的过程，只计算查找路径上的顶点与u的距离。
这样每一次需要计算的边的数量从 n 2 n^2 n2数量级缩减到 n log n n\log{n} nlogn。
OPT3 限制层次带权图层数
层次带权图M中的层数是由图的直径 k ∗ k^* k∗决定的。但是对很多图来说，图的直径会远远大于顶点之间的平均距离。
当k接近 k ∗ k^* k∗时，环上的度序列 s ( R k ( u ) ) s(R_k(u)) s(Rk(u))长度也会变得很短， f k ( u , v ) f_k(u,v) fk(u,v)和 f k − 1 ( u , v ) f_{k-1}(u,v) fk−1(u,v)会变得接近。
因此将图中的层数限制为 k ′ < k ∗ k^{'}
这样的限制显著降低构造M时的计算和存储开销。
Struc2Vec核心代码
Struc2Vec的实现相比于前面的几个算法稍微复杂一些，这里我主要说下大体思路，对一些细节有疑问的同学可以邮件或者私信我~
根据前面的算法原理介绍，首先确定一下我们要做哪些事情
- 获取每一层的顶点对距离
- 根据顶点对距离构建带权层次图
- 在带权层次图中随机游走采样顶点序列
顶点对距离计算
每一层的顶点对距离计算涉及到4个函数，我们一个一个看。。。
首先看第一个函数_get_order_degreelist_node，这个函数的作用是计算顶点root对应的有序度序列，也就是前面提到的 s ( R k ( u ) ) s(R_k(u)) s(Rk(u))。
这里我们采用层序遍历的方式从root开始进行遍历，遍历的过程计算当前访问的层次level，就是对应文章中的 k k k。每次进行节点访问时只做一件事情，就是记录该顶点的度数。
当level增加时，将当前level中的度序列(如果使用优化技巧就是压缩度序列)排序，得到有序度序列。
函数的返回值是一个字典，该字典存储着root在每一层对应的有序度序列。
第2个函数_compute_ordered_degreelist函数就很简单了，用一个循环去计算每个顶点对应的有序度序列。
def _get_order_degreelist_node(self, root, max_num_layers=None):
if max_num_layers is None:
max_num_layers = float('inf')
ordered_degree_sequence_dict = {}
visited = [False] * len(self.graph.nodes())
queue = deque()
level = 0
queue.append(root)
visited[root] = True
while (len(queue) > 0 and level <= max_num_layers):
count = len(queue)
if self.opt1_reduce_len:
degree_list = {}
else:
degree_list = []
while (count > 0):
top = queue.popleft()
node = self.idx2node[top]
degree = len(self.graph[node])
if self.opt1_reduce_len:
degree_list[degree] = degree_list.get(degree, 0) + 1
else:
degree_list.append(degree)
for nei in self.graph[node]:
nei_idx = self.node2idx[nei]
if not visited[nei_idx]:
visited[nei_idx] = True
queue.append(nei_idx)
count -= 1
if self.opt1_reduce_len:
orderd_degree_list = [(degree, freq)
for degree, freq in degree_list.items()]
orderd_degree_list.sort(key=lambda x: x[0])
else:
orderd_degree_list = sorted(degree_list)
ordered_degree_sequence_dict[level] = orderd_degree_list
level += 1
return ordered_degree_sequence_dict
def _compute_ordered_degreelist(self, max_num_layers):
degreeList = {}
vertices = self.idx # self.g.nodes()
for v in vertices:
degreeList[v] = self._get_order_degreelist_node(v, max_num_layers)
return degreeList
有了所有顶点对应的 s ( R k ( u ) ) s(R_k(u)) s(Rk(u))后，我们要做的就是计算顶点对之间的距离 g ( s ( R k ( u ) ) , s ( R k ( v ) ) ) g(s(R_k(u)), s(R_k(v))) g(s(Rk(u)),s(Rk(v)))，
然后再利用公式 f k ( u , v ) = f k − 1 ( u , v ) + g ( s ( R k ( u ) ) , s ( R k ( v ) ) ) f_k(u,v)=f_{k-1}(u,v)+g(s(R_k(u)),s(R_k(v))) fk(u,v)=fk−1(u,v)+g(s(Rk(u)),s(Rk(v)))得到顶点对之间的结构距离 f k ( u , v ) f_k(u,v) fk(u,v)
这里先看第3个函数compute_dtw_dist,该函数实现的功能是计算顶点对之间的距离 g ( s ( R k ( u ) ) , s ( R k ( v ) ) ) g(s(R_k(u)), s(R_k(v))) g(s(Rk(u)),s(Rk(v)))，参数degreeList就是前面一步我们得到的存储每个顶点在每一层的有序度序列的字典。
第4个函数convert_dtw_struc_dist的功能是根据compute_dtw_dist得到的顶点对距离完成关于 f k ( u , v ) f_k(u,v) fk(u,v)的迭代计算。
最后说明一下根据我们是否使用优化技巧self.opt2_reduce_sim_calc函数会选择计算所有顶点对间的距离，还是只计算度数接近的顶点对之间的距离。
def compute_dtw_dist(part_list, degreeList, dist_func):
dtw_dist = {}
for v1, nbs in part_list:
lists_v1 = degreeList[v1] # lists_v1 :orderd degree list of v1
for v2 in nbs:
lists_v2 = degreeList[v2] # lists_v1 :orderd degree list of v2
max_layer = min(len(lists_v1), len(lists_v2)) # valid layer
dtw_dist[v1, v2] = {}
for layer in range(0, max_layer):
dist, path = fastdtw(
lists_v1[layer], lists_v2[layer], radius=1, dist=dist_func)
dtw_dist[v1, v2][layer] = dist
return dtw_dist
def _compute_structural_distance(self, max_num_layers, workers=1, verbose=0,):
if os.path.exists(self.temp_path+'structural_dist.pkl'):
structural_dist = pd.read_pickle(
self.temp_path+'structural_dist.pkl')
else:
if self.opt1_reduce_len:
dist_func = cost_max
else:
dist_func = cost
if os.path.exists(self.temp_path + 'degreelist.pkl'):
degreeList = pd.read_pickle(self.temp_path + 'degreelist.pkl')
else:
degreeList = self._compute_ordered_degreelist(max_num_layers)
pd.to_pickle(degreeList, self.temp_path + 'degreelist.pkl')
if self.opt2_reduce_sim_calc:
degrees = self._create_vectors()
degreeListsSelected = {}
vertices = {}
n_nodes = len(self.idx)
for v in self.idx: # c:list of vertex
nbs = get_vertices(
v, len(self.graph[self.idx2node[v]]), degrees, n_nodes)
vertices[v] = nbs # store nbs
degreeListsSelected[v] = degreeList[v] # store dist
for n in nbs:
# store dist of nbs
degreeListsSelected[n] = degreeList[n]
else:
vertices = {}
for v in degreeList:
vertices[v] = [vd for vd in degreeList.keys() if vd > v]
results = Parallel(n_jobs=workers, verbose=verbose,)(
delayed(compute_dtw_dist)(part_list, degreeList, dist_func) for part_list in partition_dict(vertices, workers))
dtw_dist = dict(ChainMap(*results))
structural_dist = convert_dtw_struc_dist(dtw_dist)
pd.to_pickle(structural_dist, self.temp_path +
'structural_dist.pkl')
return structural_dist
构建带权层次图
构建带权层次图的一个主要操作就是根据前面计算得到的每一层中顶点之间的结构化距离来计算同一层中顶点之间和同一顶点在不同层之间的转移概率，通过函数_get_transition_probs实现。
layers_adj存储着每一层中每个顶点的邻接点，layers_distances存储着每一层每个顶点对的结构化距离。_get_transition_probs只做了一件事情，就是逐层的计算顶点之间的边权 w k ( u , v ) = e − f k ( u , v ) w_k(u,v)=e^{-f_k(u,v)} wk(u,v)=e−fk(u,v)，并生成后续采样需要的alias表。
def _get_transition_probs(self, layers_adj, layers_distances):
layers_alias = {}
layers_accept = {}
for layer in layers_adj:
neighbors = layers_adj[layer]
layer_distances = layers_distances[layer]
node_alias_dict = {}
node_accept_dict = {}
norm_weights = {}
for v, neighbors in neighbors.items():
e_list = []
sum_w = 0.0
for n in neighbors:
if (v, n) in layer_distances:
wd = layer_distances[v, n]
else:
wd = layer_distances[n, v]
w = np.exp(-float(wd))
e_list.append(w)
sum_w += w
e_list = [x / sum_w for x in e_list]
norm_weights[v] = e_list
accept, alias = create_alias_table(e_list)
node_alias_dict[v] = alias
node_accept_dict[v] = accept
pd.to_pickle(
norm_weights, self.temp_path + 'norm_weights_distance-layer-' + str(layer)+'.pkl')
layers_alias[layer] = node_alias_dict
layers_accept[layer] = node_accept_dict
return layers_accept, layers_alias
前面的部分仅仅得到了在同一层内，顶点之间的转移概率，那么同一个顶点在不同层之间的转移概率如何得到呢？下面的prepare_biased_walk就是计算当随机游走需要跨层时，决定向上还是向下所用到的 Γ k ( u ) \Gamma_{k}(u) Γk(u)。
w ( u k , u k + 1 ) = log ( Γ k ( u ) + e ) , k = 0 , . . . , k ∗ − 1 w(u_k,u_{k+1})=\log{(\Gamma_{k}(u)+e)},k=0,...,k^*-1 w(uk,uk+1)=log(Γk(u)+e),k=0,...,k∗−1
w ( u k , u k − 1 ) = 1 , w(u_k,u_{k-1})=1, w(uk,uk−1)=1,
def prepare_biased_walk(self,):
sum_weights = {}
sum_edges = {}
average_weight = {}
gamma = {}
layer = 0
while (os.path.exists(self.temp_path+'norm_weights_distance-layer-' + str(layer))):
probs = pd.read_pickle(
self.temp_path+'norm_weights_distance-layer-' + str(layer))
for v, list_weights in probs.items():
sum_weights.setdefault(layer, 0)
sum_edges.setdefault(layer, 0)
sum_weights[layer] += sum(list_weights)
sum_edges[layer] += len(list_weights)
average_weight[layer] = sum_weights[layer] / sum_edges[layer]
gamma.setdefault(layer, {})
for v, list_weights in probs.items():
num_neighbours = 0
for w in list_weights:
if (w > average_weight[layer]):
num_neighbours += 1
gamma[layer][v] = num_neighbours
layer += 1
pd.to_pickle(average_weight, self.temp_path + 'average_weight')
pd.to_pickle(gamma, self.temp_path + 'gamma.pkl')
随机游走采样
采样的主体框架和前面的DeepWalk,Node2Vec差不多，这里就说下不同的地方。
由于Struc2Vec是在一个多层图中进行采样，游走可能发生在同一层中，也可能发生跨层，所以要添加一些跨层处理的逻辑。
p k ( u k , u k + 1 ) = w ( u k , u k + 1 ) w ( u k , u k + 1 ) + w ( u k , u k − 1 ) p_k(u_k,u_{k+1})=\frac{w(u_k,u_{k+1})}{w(u_k,u_{k+1})+w(u_k,u_{k-1})} pk(uk,uk+1)=w(uk,uk+1)+w(uk,uk−1)w(uk,uk+1)
p k ( u k , u k − 1 ) = 1 − p k ( u k , u k + 1 ) p_k(u_k,u_{k-1})=1-p_k(u_k,u_k+1) pk(uk,uk−1)=1−pk(uk,uk+1)
def _exec_random_walk(self, graphs, layers_accept,layers_alias, v, walk_length, gamma, stay_prob=0.3):
initialLayer = 0
layer = initialLayer
path = []
path.append(self.idx2node[v])
while len(path) < walk_length:
r = random.random()
if(r < stay_prob): # same layer
v = chooseNeighbor(v, graphs, layers_alias,
layers_accept, layer)
path.append(self.idx2node[v])
else: # different layer
r = random.random()
try:
x = math.log(gamma[layer][v] + math.e)
p_moveup = (x / (x + 1))
except:
print(layer, v)
raise ValueError()
if(r > p_moveup):
if(layer > initialLayer):
layer = layer - 1
else:
if((layer + 1) in graphs and v in graphs[layer + 1]):
layer = layer + 1
return path
Struc2Vec应用
Struc2Vec应用于无权无向图(带权图的权重不会用到，有向图会当成无向图处理)，主要关注的是图中顶点的空间结构相似性，这里我们采用论文中使用的一个数据集。该数据集是一个机场流量的数据集，顶点表示机场，边表示两个机场之间存在航班。机场会被打上活跃等级的标签。
这里我们用基于空间结构相似的Struc2Vec和基于近邻相似的Node2Vec做一个对比实验。
本例中的训练，评测和可视化的完整代码在下面的git仓库中，
https://github.com/shenweichen/GraphEmbedding
分类
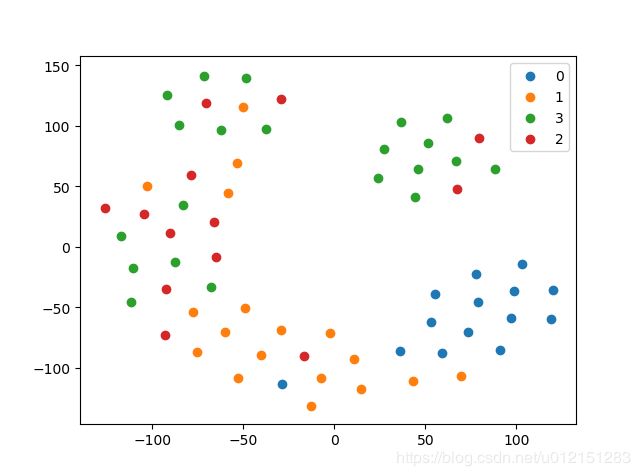
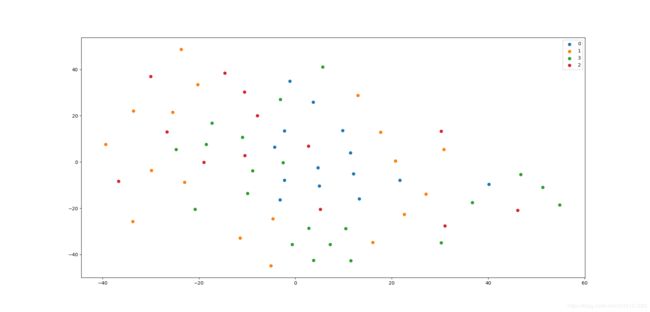
- Struc2Vec结果
micro-F1: 0.7143, macro-F1: 0.7357 - Node2Vec结果
micro-F1: 0.3571, macro-F1: 0.3445
差距还是蛮大的，说明Struc2Vec确实能够更好的捕获空间结构性。
可视化
- Struc2Vec结果
- Node2Vec结果
参考资料
- struc2vec: Learning Node Representations from Structural Identity
想要了解更多关于GraphEmbedding算法的同学，欢迎大家关注我的公众号 浅梦的学习笔记，关注后回复“加群”一起参与讨论交流！
. . . . . . . 