leetcode之Maximum Product Subarray
题目:
Find the contiguous subarray within an array (containing at least one number) which has the largest product.
For example, given the array [2,3,-2,4],
the contiguous subarray [2,3] has the largest product = 6.
思路:
解决这个问题,想到一个类似的题目,参见维基百科 最大子数列问题。
最大子数列问题的目标是在数列的一维方向找到一个连续的子数列,使该子数列的和最大。例如,对一个数列 −2, 1, −3, 4, −1, 2, 1, −5, 4,其连续子数列中和最大的是 4, −1, 2, 1, 其和为6。
笨人,就动笔吧。设置二维数组,存放以每个元素开始,相邻的元素累积和,然后比较得出最大值。
代码如下:
#include
int max_subarray(int A[], int n)
{//求最大子数列和,粗暴版
int result[n][n],max = A[0],i,j,k,low,high;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if(i < j)
result[i][j] = 0;
if(i == j)
result[i][j] = A[j];
else
result[i][j] = result[i][j-1] + A[j];
printf("%d ",result[i][j]);
}
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if(max < result[i][j])
{
max = result[i][j];
low = i;
high = j;
}
}
printf("\n最长子序列: ");
for(k = low; k <= high; k++)
printf("%d,",A[k]);
return max;
}
int main(void)
{
int A[9] = {-2,1,-3,4,-1,2,1,-5,4};
printf("\n最长子序列的和是%d: ",max_subarray(A,9));
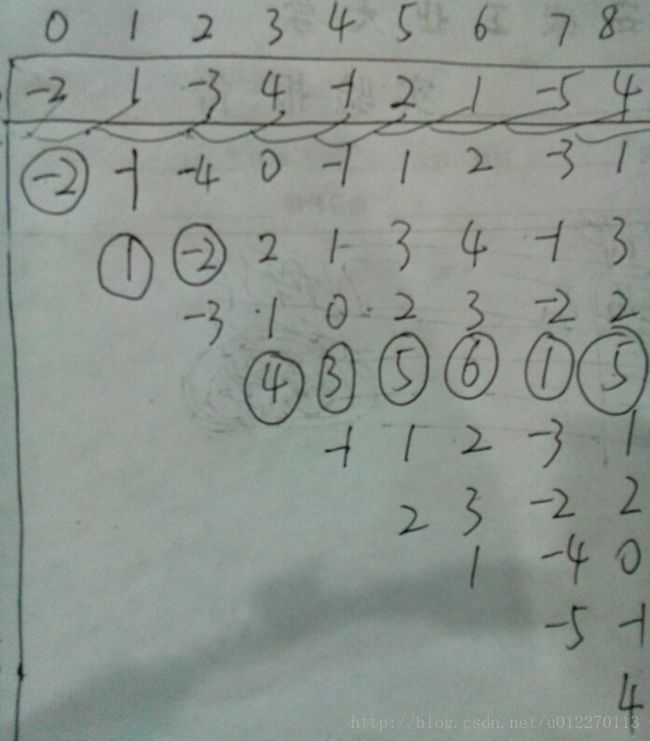
} 时间复杂度O(n^2),太大。仔细观察,发现图中每一列的最大值容易得出(在下图每列中圈出来了)。如果利用一维数组result[i],存放到当前下标i的所有连续子序列的最大和,那么就降维减少时间复杂度了。由此,体现的是动态规划思想。
那么,问题来了,怎么求result[i]?
初始值:sum[i] = A[i];
sum[i] = max(sum[i-1] + A[i],sum[i])。简化之后得出:
if(sum[i -1] > 0) sum[i-1]+ A[i] > sum[i](因为初始化时,sum[i] = A[i]).then sum[i] = sum[i-1]+ A[i] ;
else sum[i-1] < 0 sum[i] = A[i]不改变。
代码如下:
int main(void)
{
int A[9] = {-2,1,-3,4,-1,2,1,-5,4};
printf("\n最长子序列的和是%d: ",max_subarray(A,9));
}
int max_subarray(int A[], int n)
{//求最大子数列和,优化版
int result[n],max = A[0],i,j;
for(j = 0; j < n; j++)//初始化result数组,该数组存放以位置i为终点的子数列的最大和
{
result[j] = A[j];
}
for(i = 1; i < n; i++)
{
result[i] = result[i-1] > 0 ? result[i-1] + result[i] :result[i];
if(max < result[i])
{
max = result[i];
}
}
return max;
} 回到本题,不是求连续和求乘积,变数多了。没招,先来简单粗暴的吧。
代码如下
#include
int maxProduct_subarray(int A[], int n)
{//最大连续子数列乘积,粗暴版
int result[n][n],max = A[0],i,j,k,low,high;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if(i < j)
result[i][j] = 0;
if(i == j)
result[i][j] = A[j];
else
result[i][j] = result[i][j-1] * A[j];
printf("%d ",result[i][j]);
}
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if(max < result[i][j])
{
max = result[i][j];
low = i;
high = j;
}
}
printf("\n最长子序列: ");
for(k = low; k <= high; k++)
printf("%d,",A[k]);
return max;
}
int main(void)
{
//int A[9] = {-2,1,-3,4,-1,2,1,-5,4};
int A[9] = {2,3,-2,4};
printf("\n最长子序列的乘积和是%d: ",maxProduct_subarray(A,9));
}
仔细思考,当前的最值是需要比较三个数的。
初始化 localmin[i] = localmax[i] = A[i];
localmin[i] = min(A[i],localmin[i-1]*A[i],localmax[i-1]*A[i]);
localmax[i] = max(A[i],localmin[i-1]*A[i],localmax[i-1]*A[i]);
最终只需要比较局部最大值的数组localmax就可以。
代码如下:
#include
#include
int maxProduct_subarray(int A[], int n)
{//最大连续子数列乘积,优化版
int localmax[n],max = A[0],i,j,tempmin,tempmax,localmin[n];
for(j = 0; j < n; j++)
{
localmax[j] = A[j];//初始化localmax数组,该数组存放以位置i为终点的子数列的最大乘积和
localmin[j] = A[j];//初始化localmin数组,该数组存放以位置i为终点的子数列的最小乘积和
}
for(i = 1; i < n; i++)
{
tempmin = A[i] > localmin[i-1]*A[i] ? localmin[i-1]*A[i] : A[i];
localmin[i] = tempmin > localmax[i-1]*A[i]? localmax[i-1]*A[i] : tempmin;
tempmax = A[i] < localmin[i-1]*A[i] ? localmin[i-1]*A[i] : A[i];
localmax[i] = tempmax < localmax[i-1]*A[i]? localmax[i-1]*A[i] : tempmax;
if(max < localmax[i])
{
max = localmax[i];
}
}
return max;
}
int main(void)
{
int A[9] = {-2,1,-3,4,-1,2,1,-5,4};
// int A[9] = {2,3,-2,4};
printf("\n最长子序列的乘积和是%d: ",maxProduct_subarray(A,9));
}
最终ac,rumtime 40ms.