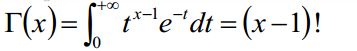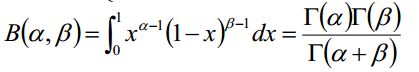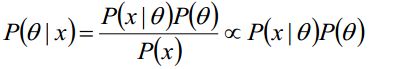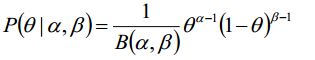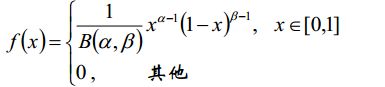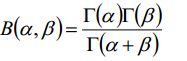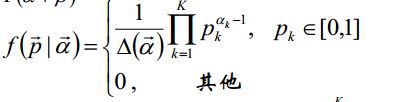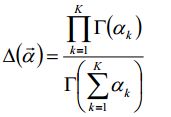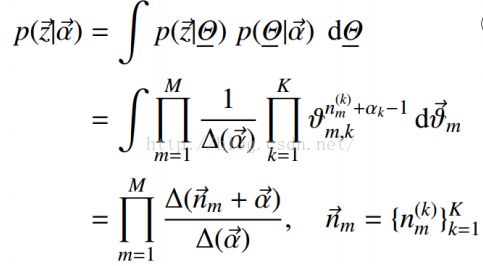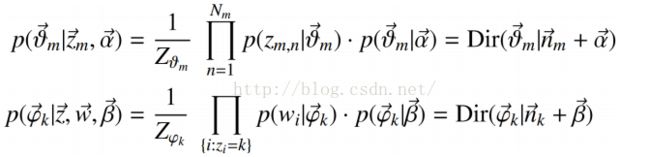LDA-隐狄利克雷分布-主题模型

注：本文中所有公式和思路来自于邹博先生的《机器学习升级版》，我只是为了加深记忆和理解写的本文。

犹豫了好久终于要开始介绍LDA了，因为其中的概念和分布关系乍一看乱糟糟的，不太容易说明白，也不知道以什么样的形式能更好的说清楚这个小东西，今天斗胆拿出自己学习的心得同大家分享，不太敢确保让读者能明白，请海涵。

矫情够了，该说说正事了！！！！

LDA模型算是pLSA模型的一个升级版吧，全程是Latent Dirichlet Allocation，从字面上可以看得出，这是一个隐藏的Dirichlet分布模型，那什么是Dirichlet分布呢？

Γ函数

既然要说Dirichlet函数，那么就不得不介绍一下Γ函数，Γ函数式欧拉发现的，举例来说Γ(4)=3!=3*2*1，其实就是一个阶乘函数，Γ函数正统的写法是这样的：

那么这个Γ函数和LDA有什么关系呢？别着急，咱们接着谈。

Beat分布

beat分布的概率密度可以如下表示：

其中系数可以这样计算或表示：

接下来我们不妨对beta的概率分布做个积分求期望：

我们可以得到这个结论，还是很漂亮的，计算过程非常简单，只有一些简单地变换而已，只是看起来有点复杂。后边就要用到这个结论。这其中就有两个参数α和β，后边也会介绍这两个参数到底是个什么鬼。

共轭分布

既然要谈LDA，还有个不得不谈共轭分布，很简单的小概念，下边的式子是贝叶斯公式：

其中P(θ|x)是后验概率，P(x|θ)是先验概率，在贝叶斯的理论体系中，如果先验概率分布和后验概率分布满足同样的分布律的话，我们就说先验分布和后验分布是共轭分布，同时，先验分布又叫做似然函数的共轭先验分布。大白话来说就是：如果一个概率分布Z乘以一个分布Y之后的分布仍然是Z，那么就是共轭分布，仅此而已。

举一个小例子来说吧：

我们都知道抛硬币实验，只有反正两种结果，我们可以认为是两点分布，做k次试验，变成二项分布，概率密度函数(似然函数)我们可以这样表示：

那么先验概率可以如下表示：

如此一来，我们就可以计算后验概率(省区了分母，如果不出输出具体概率值可以省略掉)：

从结果可以看出，先验分布和后验分布是形式是一样的，后验概率分布满足(x+α,1-x+β)的Beta分布，即伯努利分布的共轭先验分布式Beat分布。注意，千万别把共轭先验分布和共轭分布搞混淆，共轭先验分布式对于一个似然函数来说的，共轭分布是说该似然函数的先验概率和后验概率的关系是共轭。

那么这个α、β到底是什么呢？

其实是个伪计数，何为伪计数呢？

α、β是决定参数θ的超参数，这么解释吧，投硬币试验中θ是正反面的概率，那么后验概率可以如下表示：

可以很明显的看出，α、β是参数θ的指数，那么实践意义其实就是：α、β在没有任何假设的前提下，硬币朝上的概率分配，因此称之为伪计数。

如果将二项分布推广到多项呢？

共轭分布的直接推广

二项分布的共轭先验分布是Beta分布，多项分布的共轭先验分布是Dirichlet分布(终于扣题了)。

Beta分布：

其中：

Dirichlet分布：

其中：

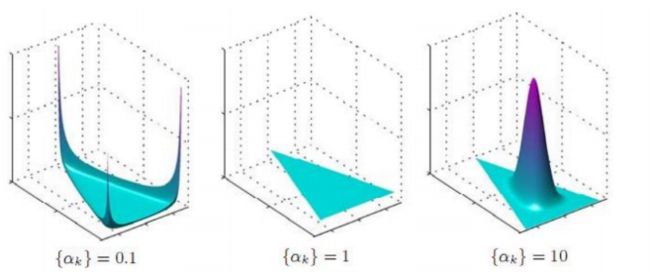
就是从2到k的一个推广，其中α是一个参数向量，共有K个，那么其中α对Dirichlet分布有何影响呢？

从上图可以看出：

当α=1时，退化为均匀分布

当α>1时，p1=p2=p3=...=pk的概率增大

当α<1时，pi=1的概率增大，p非i的概率增大

LDA的解释：

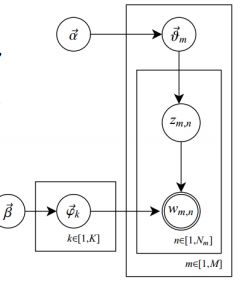
首先给大家看一张关于LDA过程的“从所周知”的图：

解释：

共有m篇文档，k个主题，每篇文档（长度为Nm）都有各自的主题分布比方说40%的武侠、30%爱情、20%科幻、其余的加起来为10%。这个分布式一个多项分布，该多项分布的参数服从Dirichlet分布，该Dirichlet的参数为α。

每个主题又有各自的词分布，词分布同样是多项分布，参数服从Dirichlet分布，参数为β。

对于每篇分档，中的第n个词的处理，首先从文档中的主题分布采样一个主题，然后在这主题的词分布中采样一个词，不断重复上述过程，知道m篇文档都完成。

那么主题和词是怎么采的呢？

这里先简单介绍一下Gibbs Sampling的过程，后边的采样文章会深入的介绍采样。

Gibbs采样

Gibbs Sampling算法的运行方式是每次概率向量的一个维度，给定其他维度的变量值采样当前维度的值，不断迭代知道收敛输出待估计的参数。

Gibbs在LDA中，初始时随机给文本中的每个词分配主题z0，然后统计每个主题出现的词t的数量以及每个文档m下出现的主题z的数量，每一轮计算，即排除当前词的主题分布，根据其他所有词的主题分布估计当前词分配各个主题的概率。

当得到当前词属于所有主题z的概率分布后，根据这个概率分布为该次采样一个新的主题。

用同样方法更新下一个词的主题，知道发现每个文档的主题分布和每个主题的词分布收敛，算法终止，输出待估计的参数θ和φ，同时每个单词的主题Zmn也可以得到。

实际中应用会设置最大迭代次数，每一次计算的公式称为Gibbs updating rule。

那么具体是怎么更新的呢？耐住性子，接着往下看。

我们知道，给定α和β，可以控制主题分布和词分布：

那么我们可以将后边的这两个因子分开来计算：

Gibbs updating rule：

那么最后的结果可以得出结论：

这个也就是我们最终写代码的式子。

我个人觉得这块其实不难，只是我们先搞清楚LDA的过程，再搞明白Gibbs的过程，那么套用思路就可以了，只不过是符号显得很复杂而已，耐心花点时间看一看，其实也就那么回事。

注意：

LDA对于短的文章来说效果不是很好，因为还没等收敛就已经结束了，我们可以通过短文拼接来改善。

终于介绍完了，细心地你一定看到我提到过“采样”，没错，采样时贝叶斯学派的做法，后续文章我将会介绍采样相关的文章。