Deep Learning学习 之 CNN代码解析(MATLAB)
MATLAB实现CNN一般会用到deepLearnToolbox-master。但是根据Git上面的说明,现在已经停止更新了,而且有很多功能也不太能够支持,具体的请大家自习看一看Git中的README。
deepLearnToolbox-master是一个深度学习matlab包,里面含有很多机器学习算法,如卷积神经网络CNN,深度信念网络DBN,自动编码AutoEncoder(堆栈SAE,卷积CAE)的作者是 Rasmus Berg Palm ([email protected])
代码下载:https://github.com/rasmusbergpalm/DeepLearnToolbox
这里我们介绍deepLearnToolbox-master中的CNN部分。
函数

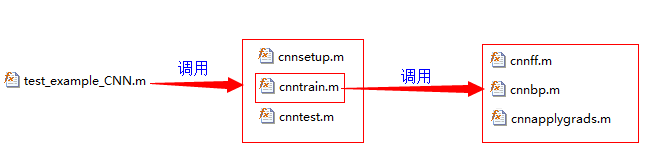
调用关系为:
该模型使用了mnist的数字mnist_uint8.mat作为训练样本,作为CNN的一个使用样例,每个样本特征为一个 28×28=的向量 。
网络结构为:
Test_example_CNN
Test_example_CNN:
- 1设置CNN的基本参数规格,如卷积、降采样层的数量,卷积核的大小、降采样的降幅
- 2 cnnsetup函数 初始化卷积核、偏置等
- 3 cnntrain函数 训练cnn,把训练数据分成batch,然后调用
- 3.1cnnff 完成训练的前向过程
- 3.2 cnnbp计算并传递神经网络的error,并计算梯度(权重的修改量)
- 3.3 cnnapplygrads 把计算出来的梯度加到原始模型上去
- 4 cnntest 函数,测试当前模型的准确率
该模型采用的数据为mnist_uint8.mat,含有70000个手写数字样本其中60000作为训练样本,10000作为测试样本。
把数据转成相应的格式,并归一化。
load mnist_uint8;
train_x = double(reshape(traub.x',28,28,60000))/255;
test_x = double(reshape(test_x',28,28,10000))/255;
train_y = double(train_y');
test_y = double(test_y');设置网络结构及训练参数
%% ex1 Train a 6c-2s-12c-2s Convolutional neural network
%% will run 1 epoch in about 200 second and get around 11% error
%% with 100 epochs you' will get around 1.2% error
rand('state',0);
cnn.layers = {
struct('type','i') %input layer
struct('type','c','outputmaps',6,'kernelsize',5) % convolution layer
struct('type','s','scale',2) %sub sampling layer
struct('type','c','outputmaps',12,'kernelsize',5) % convolutional layer
struct('type','s','scale',2) % sub sampling layer
%% 训练选项,alpha学习效率(不用),batchsiaze批训练总样本的数量,numepoches迭代次数
opts.alpha = 1;
opts.batchsize = 50;
opts.numepochs = 1;初始化网络,对数据进行批训练,验证模型准确率。
cnn = cmmsetup(cnn, train_x, train_y);
cnn = cnntrain(cnn, train_x, train_y, opts);
[er, bad] = cnntest(cnn, test_x, test_y);绘制均方误差曲线
%plot mean squared error
figure; plot(cnn.rL);Cnnsetup.m
该函数你用于初始化CNN的参数。
设置各层的mapsize大小,
初始化卷积层的卷积核、bias
尾部单层感知机的参数设置
bias统一初始化为0
权重设置为:random(-1,1)/ (6(输入神经元数量+输出神经元数量))−−−−−−−−−−−−−−−−−−−√
对于卷积核权重,输入输出为fan_in, fan_out
fan_out = net.layers{l}.outputmaps * net.layers{l}.kernelsize ^ 2;
%卷积核初始化,1层卷积为1*6个卷积核,2层卷积一共6*12=72个卷积核。对于每个卷积输出featuremap,
%fan_in = 表示该层的一个输出map,所对应的所有卷积核,包含的神经元的总数。1*25,6*25
fan_in = numInputmaps * net.layers{l}.kernelsize ^ 2;
fin =1*25 or 6*25
fout=1*6*25 or 6*12*25
net.layers{l}.k{i}{j} = (rand(net.layers{l}.kernelsize) - 0.5) * 2 * sqrt(6 / (fan_in + fan_out));
卷积降采样的参数初始化
numInputmaps = 1;
mapsize = size(squeeze(x(:, :, 1))); %[28, 28];一个行向量。x(:, :, 1)是一个训练样本。
% 下面通过传入net这个结构体来逐层构建CNN网络
for l = 1 : numel(net.layers)
if strcmp(net.layers{l}.type, 's')%降采样层sub sampling
%降采样图的大小mapsize由28*28变为14*14。net.layers{l}.scale = 2。
mapsize = mapsize / net.layers{l}.scale;
for j = 1 : numInputmaps % 一个降采样层的所有输入map,b初始化为0
net.layers{l}.b{j} = 0;
end
end
if strcmp(net.layers{l}.type, 'c')%如果是卷积层
%得到卷积层的featuremap的size,卷积层fm的大小 为 上一层大小 - 卷积核大小 + 1(步长为1的情况)
mapsize = mapsize - net.layers{l}.kernelsize + 1;
%fan_out该层的所有连接的数量 = 卷积核数 * 卷积核size = 6*(5*5),12*(5*5)
fan_out = net.layers{l}.outputmaps * net.layers{l}.kernelsioze ^ 2;
%卷积核初始化,1层卷积为1*6个卷积核,2层卷积一共有6*12=72个卷积核。
for j = 1 : net.layers{l}.outputmaps % output map
%输入做卷积
% fan_in = 本层的一个输出map所对应的所有卷积核,包含的权值的总数 = 1*25,6*25
fan_in = numInputmaps * net,layers{l}.kernelsize ^ 2;
for i = 1 : numInputmaps % input map
%卷积核的初始化生成一个5*5的卷积核,值为-1~1之间的随机数
%再乘以sqrt(6/(7*25)),sqrt(6/(18*25))
net.layers{l}.k{i}{j} = (rand(net.layers{l}.kernelsize) - 0.5 * 2 * sqrt(6 / (fan_in, fan_out)))
end
%偏置初始化为0,每个输出map只有一个bias,并非每个filter一个bias
net.layers{l}.b{j} = 0;
end
numInputmaps = net.layers{l}.outputmaps;
end
end
尾部单层感知机的参数(权重和偏量)设置
%%尾部单层感知机(全连接层)的参数设置
fvnum = prod(mapsize) * numInputmaps;%prod函数用于求数组元素的乘积,fvnum = 4*4*12 = 192,是全连接层的输入数量
onum = size(y, 1);%输出节点的数量
net.ffb = zeros(onum, 1);
net.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));cnntrain.m
该函数用于训练CNN。
生成随机序列,每次选取一个batch(50)个样本进行训练。
批训练:计算50个随机样本的梯度,求和之后一次性更新到模型权重中。
在批训练过程中调用:
Cnnff.m 完成前向过程
Cnnbp.m 完成误差传导和梯度计算过程
Cnnapplygrads.m 把计算出来的梯度加到原始模型上去
%net为网络,x是数据,y为训练目标,opts (options)为训练参數
function net = cnntrain(net, x, y, opts)
%m为图片祥本的數量,size(x) = 28*28*60000
m = size(x,3);
%batchsize为批训练时,一批所含图片样本数
nunbatches = m / opts. batchsize;%分批洲练,得到训练批次
net.rl = [];%rL是最小均方误差的平滑序列,绘图要用
for i = 1 : opts.numepochs %训练迭代
%显示训练到第几个epoch,一共多少个epoch
disp(['epoch' num2str(i) '/' num2str(opts.numepochs)]);
%Matlab自带函数randperm(n)产生1到n的整数的无重复的随机排列,可以得到无重复的随机数。
%生成m(图片数量)1~n整数的随机无重复排列,用于打乱训练顺序 .
kk = randperm(n);
for 1 = 1 : numbatches%训练每个batch
%得到训练信号,一个样本是一层x(:, :, sampleOrder),每次训练,取50个样本.
batch_x = x(:, :, kk((l-1) * opts.batchsize + 1 : l * opts.batchsize));
%教师信号,一个样本是一列
batch_y = y(:, kk((l-1) * opts.batchsize + 1 : l * opts.batchsize));
%NN信号前传导过程
net = cnnff (net, batch_x);
%计算误差并反向传导,计算梯度
net = cnnbp (net, batch_y);
%应用梯度,模型更新
net = cnnapplygrads(net, opts);
%net.L为模型的costFunction,即最小均方误差mse
%net.rL是最小均方误差的平滑序列
if isempty(net.rL)
net.rL(1) = net.L;
end
net.rL(end+1) = 0.99 * net.rL(end) + 0.01 * net.L;
end
end cnnff.m
取得CNN的输入
numLayers = numel(net.layers);
net.layers{1}.a{1} = x;%a是输入map,时一个[28, 28, 50]的矩阵(具体情况具体定)
numInputmaps = 1;两次卷积核降采样层处理
for l = 2 : numLayers %for each layer
if strcmp(net.layers{l}.type, 'c')
for j = 1 : net.layers{l}.outputmaps %for each output map
% z = zeros([28,28,50]-[4,4,0]) = zeros([24,24,50])
z = zeros(size(net.layers{l一1}.a{1}) - [net.layers{l}.kernelsize — 1, net.layers{l}.kernelsize — 1, 0]);
for i = 1 : numlnputmaps% for each input map
z = z + convn(net.layers{l-1}.a{i}, net.layers{l}.k{i}{j}, 'valid');
end
%加上bias并sigmo出来理
net.layers{l}.k{i}{j} = sigm(z + net.layers{l}.b{j});
end
%下层输入feacureMap的里等于本层输出的feateMap的数量
numlnputmaps = net.layers{l}.outputmaps;
elseif strcmp(net.layers{l}.type,'s')
%down sample
for j = 1 : numlnputmaps
%这子采样是怎么做到的?卷积一个[0.25,0,25;0.25,0,5]的卷积核,然后降采样。这里有重复计算
z = convon(net.layers{l-1}).a{j}, ones(net.layers{l}.scale) / (net.layers{l}.scale ^ 2),'valid');
%这里设置scale长度的步长,窗移一》scale,但是这里有计算浪费
net.layers{l}·a{j} = z(1 : net.layers{1}.scale : end, 1 : net.layers{l}.scale : end, :);
end
end
end尾部单层感知机的数据处理
需要把subFeatureMap2连接成为一个(4*4)*12=192的向量,但是由于采用了50样本批训练的方法,subFeatureMap2被拼合成为一个192*50的特征向量fv;
Fv作为单层感知机的输入,全连接的方式得到输出层
%尾部单层感知机的数据处理。 concatenate all end layer feature maps into vector
net.fv = [];
for j = 1 : numel(net.layers{numLayers}.a) %fv每次拼合入subFeaturemap2[j],[包含50个样本]
sa = size(net.layers{numLayers}.a{j});%size of a = sa = [4, 4, 50];得到Sfm2的一个输入图的大小
%reshape(A,m,n);
%把矩阵A改变形状,编程m行n列。(元素个数不变,原矩阵按列排成一队,再按行排成若干队)
%把所有的Sfm2拼合成为一个列向量fv,[net.fv; reshape(net.layers{numLayers}.a{j}, 4*4, 50)];
net.fv = [net.fv; reshape(net.layers{numLayers}.a{j}, sa(1) * sa(2), sa(3))]
%最后的fv是一个[16*12*50]的矩阵
end
%feedforvard into output perceptrons
%net.ffW是[10,192]的权重矩阵
%net.ffW * net.fv是一个[10,50]的矩阵
%repmat(net.ffb, 1, size(net.fv, 2)把 bias复制成50份排开
net.o = sigm(net.ffW * net.fv + repmat(net.ffb, 1, size(net.fv, 2)));cnnbp.m
该函数实现2部分功能,计算并传递误差,计算梯度
计算误差和LossFunction
numLayers = numel(net.layers);
%error
net.e = net.o - y;
% loss function 均方误差
net.L = 1 / 2 * sun(net.e(:) . ^ 2 ) / size(net.e, 2);计算尾部单层感知机的误差
net.od = net.e .* (net.o .*(1 - net.o)); %output dalta, sigmoid 误差
%fvd, feature vector delta, 特征向里误差,上一层收集下层误差,size = [192*50]
net.fvd = (net.ffW' * net.od);
%如果MLP的前一层(特征抽取最后一层)是卷积层,卷积层的输出经过sigmoid函数处理,error求导
%在数字识别这个网络中不要用到
if strcmp(net.layers{numLayers}.type, 'c')
%对于卷基层,它的特征向里误差再求导(net.fv .* (1-net.fv))
net.fvd = net.fvd .*(net.fv .* (1 - net.fv));
end改变误差矩阵形状
把单层感知机的输入层featureVector的误差矩阵,恢复为subFeatureMap2的4*4二维矩阵形式
% reshape feature vector deltas into output map style
sizeA = size(net.layers{numlayers}.a{1}));%size(a{1}) = [4*4*50],一共有a{1}~a{12};
fvnum = sizeA(1) * sizeA(2); %fvnum一个图所含有的特征向量的数量,4*4
for j = 1 : numel(net.layers{numLayers}.a) %subFeatureMap2的数量,1:12
%net最后一层的delta,由特征向量delta,侬次取一个featureMap大小,然后组台成为一个featureMap的形状
%在fvd里面亻呆存的是所有祥本的特征向量(在cnnff.m函数中用特征map拉成的);这里需要重新变換回来持征map的 形式。
%net.fvd(((j - 1) * fvnum + 1) : j * fvnum, : ) ,一个featureMap的误差d
net.layers{numLayers}.d{j} = reshape(net.fvd(((j-1) * fvnum + 1);j * fvnum, :), sizeA(1), sizeA(2), sizeA(3));
%size(net.layers{numLayers}.d{j}) = [4 * 4 * 50]
%size(net.fvd) = [192 * 50]
end插播一张图片:
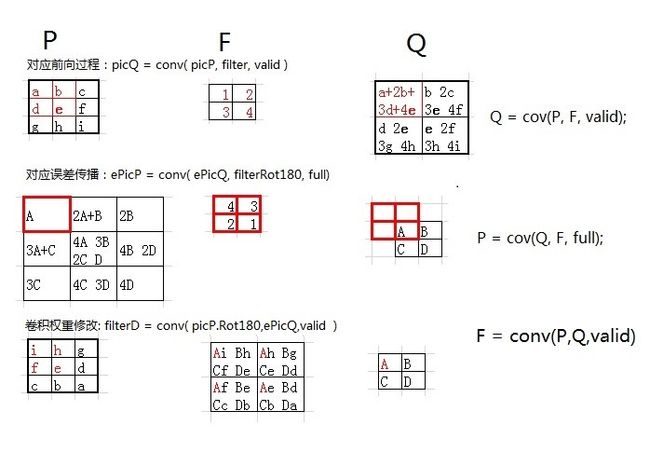
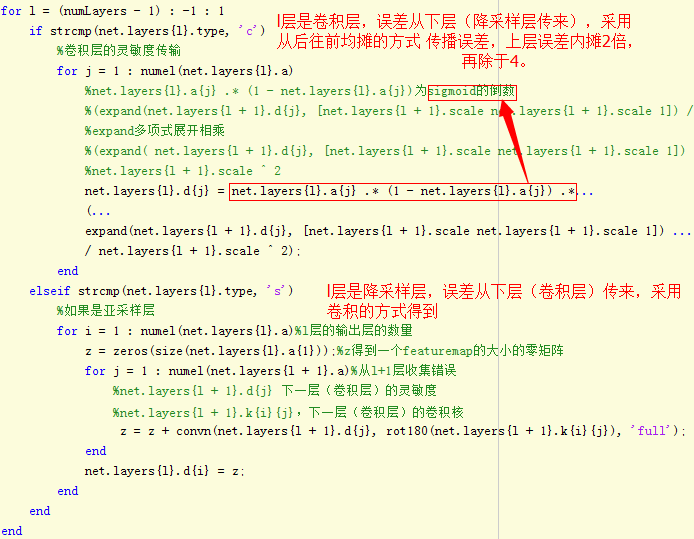
误差在特征提取网络【卷积降采样层】的传播
如果本层是卷积层,它的误差是从后一层(降采样层)传过来,误差传播实际上是用降采样的反向过程,也就是降采样层的误差复制为2*2=4份。卷积层的输入是经过sigmoid处理的,所以,从降采样层扩充来的误差要经过sigmoid求导处理。
如果本层是降采样层,他的误差是从后一层(卷积层)传过来,误差传播实际是用卷积的反向过程,也就是卷积层的误差,反卷积(卷积核转180度)卷积层的误差,原理参看插图。
计算特征抽取层和尾部单层感知机的梯度
%计算特征抽取层(卷积+降采样)的梯度
for l = 2 : numLayers
if strcmp(net.layers{l}.type, 'c') %卷积层
for j = 1 : numel(net.layers{l}.a) %l层的featureMap的数量
for i = 1 : numel(net.layers{l - 1}.a) %l-1层的featureMap的数量
%卷积核的修改量 = 输入图像 * 输出图像的delta
net.layers{l}.dk{i}{j} = convn(flipall(net.layers{l - 1}.a{i}), net.layers{l}.d{j}, 'valid') / size(net.layers{l}.d{j}, 3);
end
%net.layers.d{j}(:)是一个24*24*50的矩阵,db仅除于50
net.layers{l}.db{j} = sum{net.layers{l}.d{j}(:)} / size(net.layers{l}.d{j}, 3);
end
end
end
%计算机尾部单层感知机的梯度
%sizeof(net.od) = [10, 50]
%修改量,求和除于50(batch大小)
net.dffW = net.od * (net.fv)' / size(net.od, 2);
net.dffb = mean(net.od. 2);%第二维度取均值cnnapplygrads.m
该函数完成权重修改,更新模型的功能
1更新特征抽取层的权重 weight+bias
2 更新末尾单层感知机的权重 weight+bias
function net = cnnapplygrads(net, opts) %使用梯度
%特征抽取层(卷机降采样)的权重更新
for l = 2 : numel(net.layers) %从第二层开始
if strcmp(net.layers{l}.type, 'c')%对于每个卷积层
for j = 1 : numel(net.layers{l}.a)%枚举该层的每个输出
%枚举所有卷积核net.layers{l}.k{ii}{j}
for ii = 1 : numel(net.layers{l - 1}.a)%枚举上层的每个输出
net.layers{l}.k{ii}{j} = net.layers{l}.k{ii}{j} - opts.alpha * met.layers{l}.dk{ii}{j};
end
%修正bias
net.layers{l}.b{j} = net.layers{l}.b{j} - opts.alpha * net.layers{l}.db{j};
end
end
end
%单层感知机的权重更新
net.ffW = net.ffW - opts.alpha * net.dffW;
net.ffb = net.ffb - opts.alpha * net.dffb;
endcnntest.m
验证测试样本的准确率
%验证测试样本的准确率
function [er, bad] = cnntest(net, x, y)
% feedforward
net = cnnff(net, x);
[~, h] = max(net.o);
[~, a] = max(y);
%find(x) FIND indices of nonzero elements
bad = find(h ~= a); %计算预测错误的样本数量
er = numel(bad) / size(y, 2); % 计算错误率
end