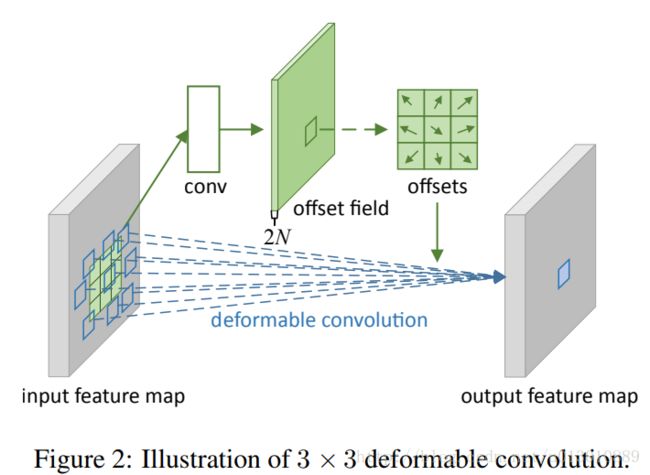
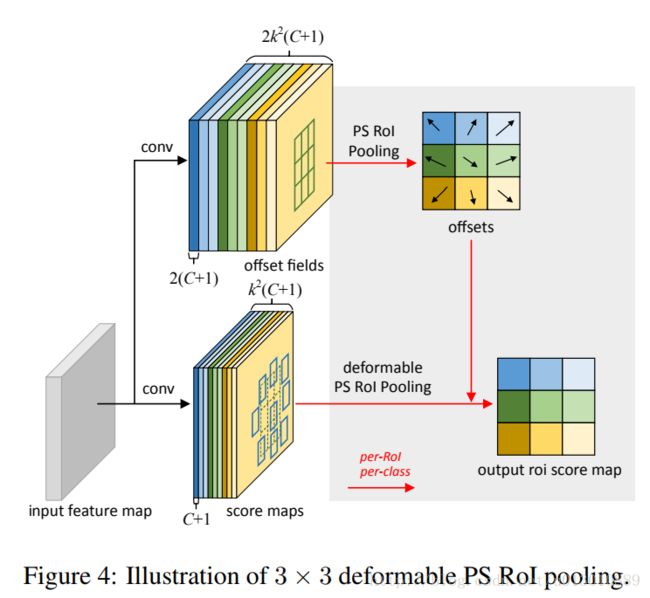
Deformable Convolutional Networks解读

这篇论文是daijifeng老师又一篇好文，一贯的好想法，而且实现的很漂亮，arxiv link

Motivation

现实图片中的物体变化很多，之前只能通过数据增强来使网络“记住”这些变种如n object scale, pose, viewpoint, and part deformation，但是这种数据增强只能依赖一些先验知识比如反转后物体类别不变等，但是有些变化是未知而且手动设计太不灵活，不易泛化和迁移。本文就从cnn model的基础结构入手，比如卷积采样时位置是固定的，pool时采样位置也是固定，roi pool也是把roi分成固定的空间bins，这些它就不能处理几何的变化，出现了一些问题，比如编码语义或者空间信息的高层神经元不希望同一层的每个激活单元元的感受野是一样的。在检测中都是以bbox提取特征，这对于非格子的物体是不利的。因此本文提出了可变形的卷积神经网络。

举例: 3x3的卷积或pool，正常的cnn网络采样固定的9个点，而改进后，这九个采样点是可以变形的，特殊的情况如©是放大了(d)是旋转了

实现

普通cnn

以3x3卷积为例
对于每个输出y(p0)，都要从x上采样9个位置，这9个位置都在中心位置x(p0)向四周扩散得到的gird形状上，(-1,-1)代表x(p0)的左上角，(1,1)代表x(p0)的右下角，其他类似。

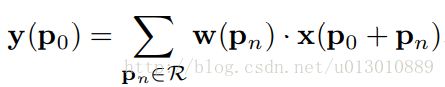
可变形cnn

同样对于每个输出y(p0)，都要从x上采样9个位置，这9个位置是中心位置x(p0)向四周扩散得到的，但是多了一个新的参数 ∆pn，允许采样点扩散成非gird形状

注意∆pn很有可能是小数，而feature map x上都是整数位置，这时候需要双线性插值

这个地方不仅需要反传w(pn) x(p0 + pn + ∆pn)的梯度，还需要反传∆pn的梯度，需要仔细介绍下双线性插值

双线性插值

线性插值

已知数据 (x0, y0) 与 (x1, y1)，要计算 [x0, x1] 区间内某一位置 x 在直线上的y值(或某一位置y子啊直线上的x值，类似)
用x和x0，x1的距离作为一个权重，用于y0和y1的加权

双线性插值

双线性插值本质上就是在两个方向上做线性插值。
x§的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分，u、v为浮点坐标的小数部分，是取值[0,1)区间的浮点数)，则这个点的像素值x§: (i+u,j+v) 可由坐标为 x(q1): (i,j)、x(q2): (i+1,j)、x(q3): (i,j+1)、x(q4): (i+1,j+1)所对应的周围四个像素的值决定

1. 先在x方向上做线性插值得到t1 t2的像素值
2. 再在y方向做线性插值最终得到x§的像素值
   最终公式:

f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) (一)

对应到可变形卷积上求x§


g(a, b) = max(0, 1 − |a − b|). q就是临近的4个点, p0,pn,∆pn都是二维坐标,可带入公式一

然后求导求梯度

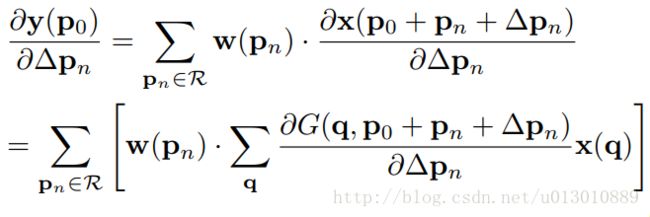
∂G(q,p0+pn+∆pn) / ∂∆pn 可由公式一求出

结构

Deformable Convolution

这个offset是通过在input feature上加个卷积，这个卷积的大小和dilation和本身的卷积是一致的。

The output offset fields have the same spatial resolution with the input feature map
我对这句话有异议，应该是和输出的feature map大小一致吧。对于每个输出feature map上的每个点都有2*3*3个偏移值。加上上一句这个卷积的大小和dilation和本身的卷积是一致的当然和输出的feature map大小一致了，代码里也是这样体现的

res5a_branch2a_relu = mx.symbol.Activation(name='res5a_branch2a_relu', data=scale5a_branch2a, act_type='relu')
# 和DeformableConvolution卷积的参数都一致 
# num_filter=num_deformable_group * 2 * kernel_height * kernel_width 
# num_deformable_group可忽略，类似于组卷积，所以72/4=18=2*3*3
res5a_branch2b_offset = mx.symbol.Convolution(name='res5a_branch2b_offset', data=res5a_branch2a_relu,num_filter=72, pad=(2, 2), kernel=(3, 3), stride=(1, 1), dilate=(2, 2), cudnn_off=True)

res5a_branch2b = mx.contrib.symbol.DeformableConvolution(name='res5a_branch2b', data=res5a_branch2a_relu, offset=res5a_branch2b_offset,num_filter=512, pad=(2, 2), kernel=(3, 3), num_deformable_group=4, stride=(1, 1), dilate=(2, 2), no_bias=True)

Deformable RoI Pooling

RoI Pooling

首先，RoI池化(方程(5))生成池化后的特征映射。从特征映射中，一个fc层产生归一化偏移量ΔpˆijΔp^{ij，然后通过与RoI的宽和高进行逐元素的相乘将其转换为方程(6)中的偏移量ΔpijΔpij，如：Δpij=γ⋅Δpˆij∘(w,h)Δpij=γ⋅Δp}ij∘(w,h)。这里γγ是一个预定义的标量来调节偏移的大小。它经验地设定为γ=0.1γ=0.1。为了使偏移学习对RoI大小具有不变性，偏移归一化是必要的。这部分不是太理解。

Position-Sensitive (PS) RoI Pooling

# 用1*1的卷积得到offset 2K*k(C+1)
rfcn_cls_offset_t = mx.sym.Convolution(data=relu_new_1, kernel=(1, 1), num_filter=2 * 7 * 7 * num_classes, name="rfcn_cls_offset_t")

rfcn_bbox_offset_t = mx.sym.Convolution(data=relu_new_1, kernel=(1, 1), num_filter=7 * 7 * 2, name="rfcn_bbox_offset_t")

参考:
Deformable_Convolutional_Networks_Oral
[图像缩放——双线性插值算法(http://blog.csdn.net/xiaqunfeng123/article/details/17362881)
三十分钟理解：线性插值，双线性插值Bilinear Interpolation算法
Deformable Convolutional Networks论文翻译——中英文对照
代码: msracver/Deformable-ConvNets