白话数据结构之【树状数组】

百度百科：

树状数组(Binary Indexed Tree(BIT), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有

元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值。

这种数据结构（算法）并没有C++和Java的库支持，需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组

和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组

效率要高很多。但使用范围比线段树小（如查询每个区间最小值问题需要线段树）;

深度剖析：

如果给定一个数组，要你求里面所有数的和，一般都会想到累加。但是当那个数组很大的时候，累加就显得太耗时了，时间复杂度为O(n)，

并且采用累加的方法还有一个局限，那就是，当修改掉数组中的元素后，仍然要你求数组中某段元素的和，就显得麻烦了。所以我们就要用到树状数组，

他的时间复杂度为O（lgn），相比之下就快得多。

下面就讲一下什么是树状数组：
一般讲到树状数组都会少不了下面这个图：

 

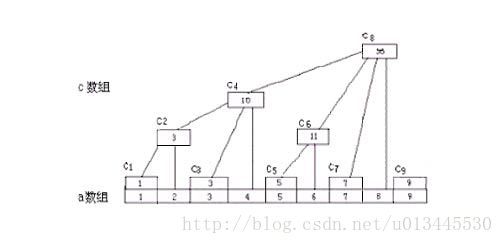
下面来分析一下上面那个图看能得出什么规律：

 据图可知：c1=a1，c2=a1+a2，c3=a3，c4=a1+a2+a3+a4，c5=a5，c6=a5+a6，c7=a7，

c8=a1+a2+a3+a4+a5+a6+a7+a8，c9=a9，c10=a9+a10，c11=a11.......

.c16=a1+a2+a3+a4+a5+.......+a16。
 分析上面的几组式子可知，当 i 为奇数时，ci=ai ；当 i 为偶数时，就要看 i 的因子中最多有二的多少次幂，

例如，6 的因子中有 2 的一次幂，等于 2 ，所以 c6=a5+a6（由六向前数两个数的和），4 的因子中有 2 的两次幂，等于 4 

所以 c4=a1+a2+a3+a4（由四向前数四个数的和）。

(一)有公式：cn=a(n-a^k+1)+.........+an（其中 k 为 n 的二进制表示中从右往左数的 0 的个数）。

那么，如何求 a^k 呢？求法如下：

int lowbit(int x)
{
      return x&(-x);    //这个神奇的公式是怎么推出来的我也不知道，你用补码算一下是正确的，伟大的公式ｏｒｚ。。
}

lowbit（）的返回值就是 x中的因子中最多有二的多ｋ次幂 的2^k 次方的值。


求出来 2^k 之后，数组 c 的值就都出来了，接下来我们要求数组中所有元素的和。
(二）求数组的和的算法如下：

(1）首先，令sum=0，转向第二步；

(2）接下来判断，如果 n>0 的话，就令sum=sum+cn转向第三步，否则的话，终止算法，返回 sum 的值；

(3）n=n - lowbit（n）（将n的二进制表示的最后一个零删掉），回第二步。

代码实现：

int Sum(int n)
{
    int sum=0;
    while(n>0)
    {
         sum+=c[n];
         n=n-lowbit(n);
    }    
    return sum;
}

比如我们现在求１－10的和，先算出数组ｃ
c[1] = a1 = 1;
c[2] = a1+a2 = 1+2 = 3;
c[3] = a3 = 3;
c[4] = a1+a2+a3+a4 = 1+2+3+4 = 10;
c[5] = a5 = 5;
c[6] = a6+a5 = 6+5 = 11;
c[7] =a7 = 7;
c[8] =  a1+a2+a3+a4+a5+a6+a7+a8 = (1+8)*8/2=36;
c[9] = a9 = 9;
c[10] =  a9+a10= 9+10=19;
….
sum += c[10];(现在代表sum = a9+a10);
n = n -lowbit(10);(n = 10 – 2 = 8)

sum += c[8] (现在代表sum = a9+a10+a1+...+a8);
n = n -lowbit(10);(n = 8 – 2 = 0)
结束
你看两步就可以得到结果（别给我说你用高斯公式做。。我现在只是拿这个简单的例子将树状数组）；
这个时间复杂度可以优化到logn级
还有如果修改其中的某个值也很快
还是拿上面的例子作比较，现在我将a5 = 5修改成a5 = 50;
那么我们只需要将还有a5的区间全部加４５，比如以前c[5],c[6],c[8]这两个区间包含a5，那么就把这两个区间都加上４５
代码如下：

void change(int i,int x)
{
     while(i<=n)
     {
          c[i]=c[i]+x;
          i=i+lowbit(i);
     }
}

n = 9;
输入i = 5,x = 45;
c[5] = 5+45 = 50;
i= 5+1 = 6;

c[6] = a5+a6+45;
I = 6+2 = 8;

c[8] = a1+..+a8+45;
I = 8 + 8 = 16;
i > n 退出
修改完以后再次求和就可以体现树状数组的强大所在了
现在举例题深度理解：

Ｈｄｕ1166

题意:

第一行一个整数T，表示有T组数据。 
每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。 
接下来每行有一条命令，命令有4种形式： 
(1) Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30） 
(2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）; 
(3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数; 
(4)End 表示结束，这条命令在每组数据最后出现; 
每组数据最多有40000条命令 

output:

对第i组数据,首先输出“Case i:”和回车, 
对于每个Query询问，输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。 

Sample Input

1 10 1 2 3 4 5 6 7 8 9 10 Query 1 3 Add 3 6 Query 2 7 Sub 10 2 Add 6 3 Query 3 10 End

 

Sample Output

Case 1: 6 33 59

 

这是一道模板题：请直接分析代码即可,注意这种题目cin和cout容易ＴＬＥ

#include 
#include 
#include 
#include 
using namespace std;

int N;
int a[50010];
int c[50010];

int lowbit(int x)
{
    return x&-x;
}

void update(int i , int num)
{
    while(i <=  N)
    {
        c[i] += num;
        i += lowbit(i);
    }
}

int getsum(int x)
{
    int sum = 0;

    while(x > 0)
    {
        sum += c[x];
        x -= lowbit(x);
    }

    return sum;
}

int main()
{
    int t,z;
    scanf("%d",&t);
    z = 1;
    while(t--)
    {
        scanf("%d",&N);

        memset(c,0,sizeof(c));

        for(int i = 1; i <= N; i++)
        {
            int m;
         
           scanf("%d",&m);
            update(i,m);
        }
        printf("Case %d:\n",z++);
        char str[10];
        while(scanf("%s",str) && str[0] != 'E')
        {

            if(str[0] == 'Q')
            {
                int i,j;
                 scanf("%d%d",&i,&j);
               printf("%d\n",getsum(j) - getsum(i-1));

            }
            else if(str[0] == 'A')
            {
                int x,y;
                scanf("%d%d",&x,&y);
                update(x,y);
            }
            else if(str[0] == 'S')
            {
                int p,q;
                scanf("%d%d",&p,&q);
                update(p,-q);
            }

        }

    }
    return 0;
}

如果还有什么不懂的或者有疑问的地方敬请沟通！