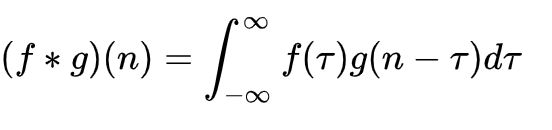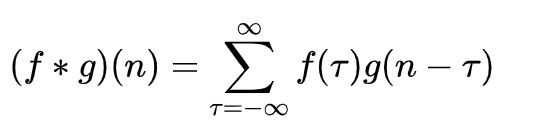【超简明】通俗解释CNN-卷积-图片识别-TF实现-数据可视化【人工智能学习】

这几天在做一个【python入门语法】和【Django全栈开发】的互动课程，就把AI算法实现系列文章落下了…
我感觉我再补充几个算法和数学原理文章，AI的系列课程也可以开始做了，希望大家多多捧场！
今天补充一个，经典的CNN结构！

目标：提高速度

说到神经网路，我们已经学了四关了，相信大家对于【网络结构】的重要性肯定了解了。

不同的神经网络的作用只有一个：加快运算速度！

深层神经网络和浅层神经网络相比，在速度上就有所突破，但是对于更庞大的数据，比如说图片数据、视频数据来说，这种突破带来的优化微乎其微。
对于图片而言，比如说一个分辨率200x200的三通道（RGB）图片，他的数据就有200x200x3，再如果有10000条数据，那么他的数据量就有 200x200x3x10000 之多！（各类算法的复杂度具体计算方法，请看链接文章【DNN/CNN/RNN复杂度评估】）

深度学习的深度没有固定的定义，2006年Hinton解决了局部最优解问题，将隐含层发展到7层，这达到了深度学习上所说的真正深度。不同问题的解决所需要的隐含层数自然也是不相同的，一般语音识别4层就可以，而图像识别20层屡见不鲜。但随着层数的增加，又出现了参数爆炸增长的问题。假设输入的图片是1K*1K的图片，隐含层就有1M个节点，会有10^12个权重需要调节，这将容易导致过度拟合和局部最优解问题的出现。为了解决上述问题，提出了CNN。

面对如此庞大的数据，我们直接用DNN（深度神经网络）虽然可以达成效果，但是，计算速度始终难以突破，那么我们就要想办法去【降低参与计算的参数】

面对图像问题，我们进行了一系列思考，DNN是模拟了人的【神经元网络】，相当于大脑的功能，那么既然我们面对图像的是看图，那么我们是不是可以参考视觉的大脑皮层结构呢？？

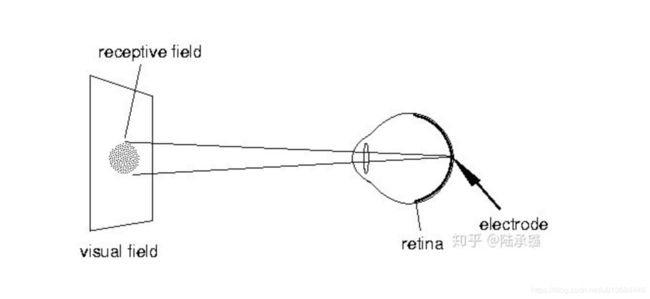
他来了他来了，他带着算法走来了！
Hubel 和Wiesel1968年做的实验是很有影响力的，具体的就不说了，有兴趣的同学可以看这个科学史，反正它发现，视觉皮层对于信息的处理，做了一个很NB的操作：【特征提取】，行话叫做 【过滤】 ！

通俗解释吧，就是进行了以下操作：

1. 不看单个像素信息，而是直接看一片
2. 这个一片不是全部图像，而是【盲人摸象】一般由无数个小片段组成
3. 每个小片段我们抽象一个平均结果，就是知道他大概是个啥，比如说知道这里是竖线，这里是一大片黄色等等…这些抽象后的大概结果组成了我们新的图片，给下一层神经
4. 这一层受到了上面的指令，就继续这样拆分，找出最大特征和匹配，形成结果再给下一层
5. 最后一层收到的结果就是是我们提取的特征了！然后在大脑中匹配一些列可能的选项，可能是xxx的概率分别是多少，然后给出判断。

总之，我们通过视觉认识事物的方式，就是通过几次*几层的【盲人摸象】来搞定的。

再解释一边：想象一下，我们现在是个【盲人皇帝】，命令一大堆的工人给我们当眼睛，他们每个人首先描述一小块的最重要特征告诉我，我们就很快得出结论，至少要比按像素要快很多…
然后我们这个工人描述特征的层级再多一点，由【浅层】到【深层】来加快我们的判断，这个方法就叫做 「卷积神经网络」

每个小工人就是「卷积神经元」，每一批工人处理出来结果给下一批，就是不同层的神经网络。

卷积+池化就是工人提取特征的方式：

1. 卷积——提取特征
   卷积层的运算过程如下图，用一个卷积核扫完整张图片：
   
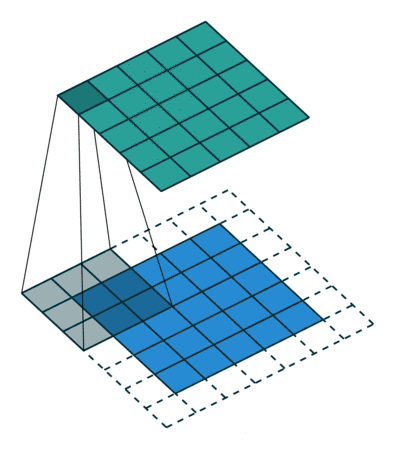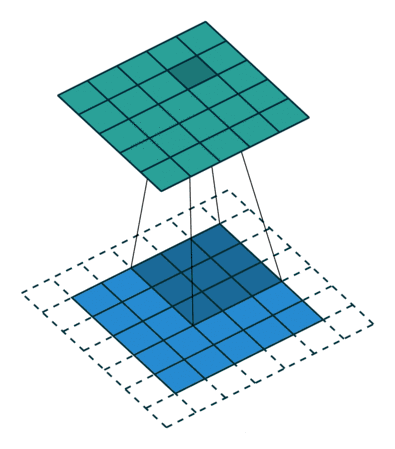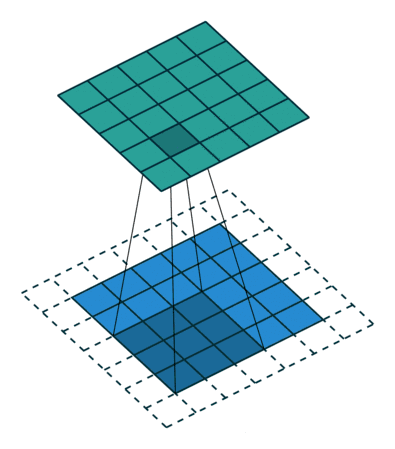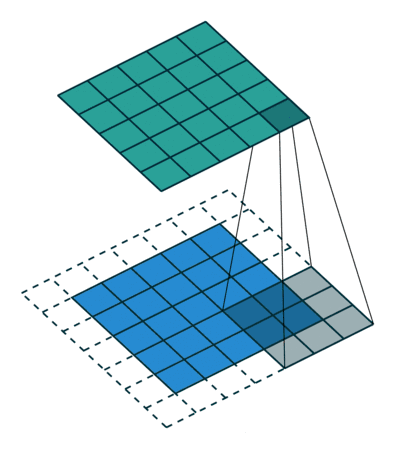
   解释一下，下面蓝色是输入的图，绿色是卷积之后的图，外侧的虚线补充的是人工添加的数据，目的是扫描的全一点。
   这样，我们就得到了一个绿色的卷积输出结果！

但是还没结束，因为它的数据量还没有变化，我们需要让自己【近视眼】一下，将一大片的卷积结果变成一个！这样的【特征降维】的操作就是池化

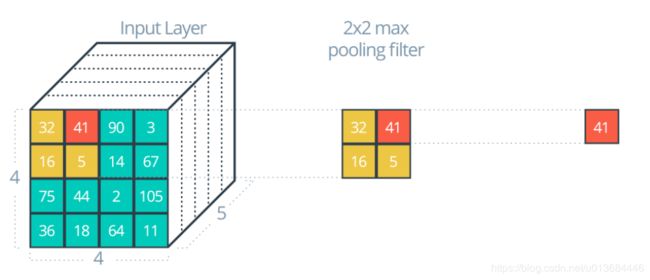
我们上面的，就是一个2*2池化Max矩阵，就是选择这里最大值输出（简单粗暴但有用），连续操作之后就变成了下图

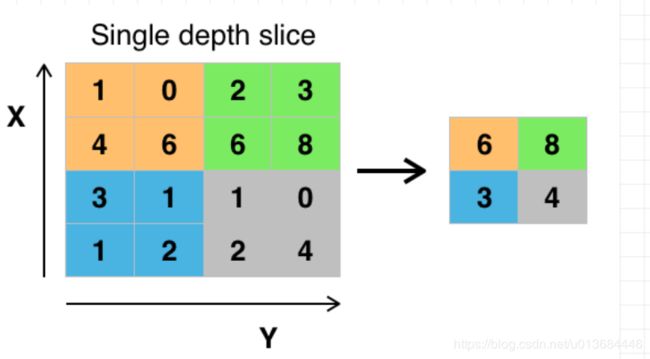
然后把这个结果继续传给下一层的卷积+池化…和DNN一个操作。最后根据结果的Label进行匹配【最大似然结果】，输出结果～

提问：浅层和深层神经网络的优化是在优化 每个神经元的权重值 ，那么在CNN中我们要优化什么呢？？？
思考…
.
.
.
…
.
.
…
.
.
…
.
.
好的，公布答案，是…卷积核中的权重！

这就要深入到具体的卷积计算了，先来一段天书，不过你之后要慢慢会看哦卷积，是我们学习高等数学之后，新接触的一种运算，因为涉及到积分、级数，所以看起来觉得很复杂。

卷积运算

我们称 (f*g)(n) 为 f,g 的卷积

其连续的定义为：

其离散的定义为：

这两个式子有一个共同的特征：

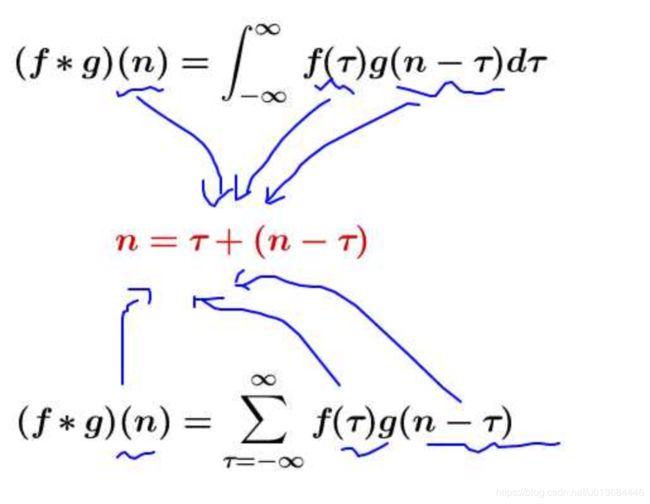
这个特征有什么意义？

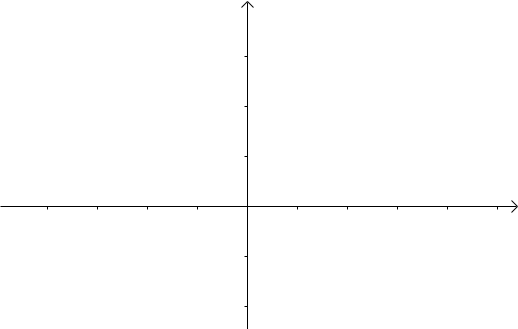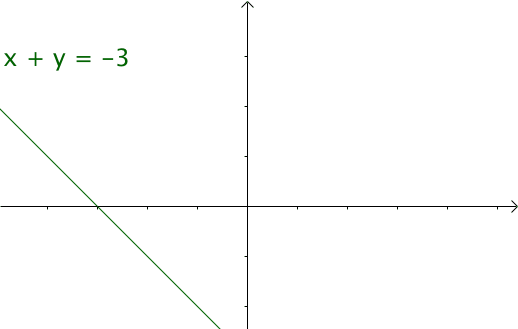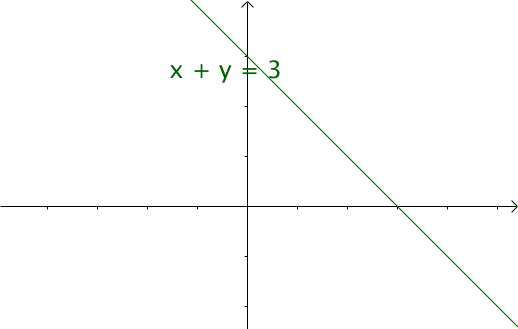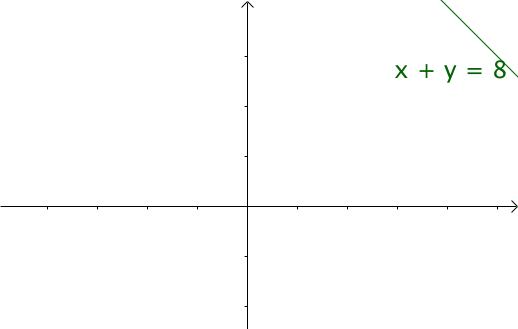如果遍历这些直线，就好比，把毛巾沿着角卷起来：

只看数学符号，卷积是抽象的，不好理解的，但是，我们可以通过现实中的意义，来习惯卷积这种运算，正如我们小学的时候，学习加减乘除需要各种苹果、糖果来帮助我们习惯一样。

以上卷积运算摘自参考文章卷积运算 - Bill Yuan - 博客园，文章内讲解更详细，相关卷积运算理解请点击查看。

但是我们看到一个关键信息：卷积操作是【乘操作】！a为输入，f为卷积，c为输出示例：

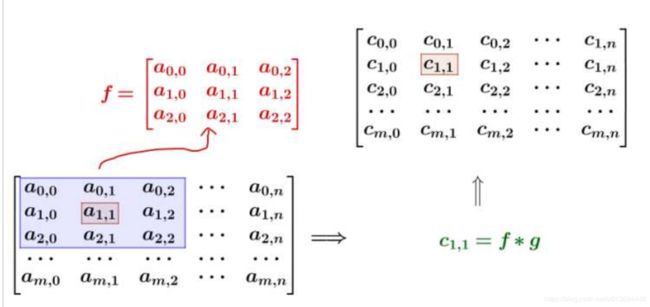
经过计算得到的新图像，那么我们的【卷积动图加数据】就是这样的：

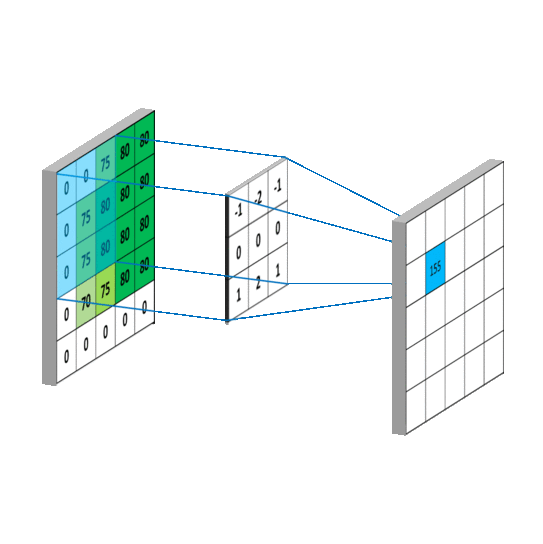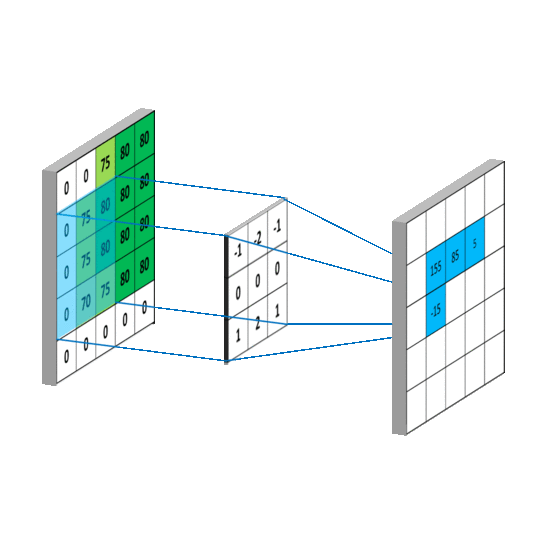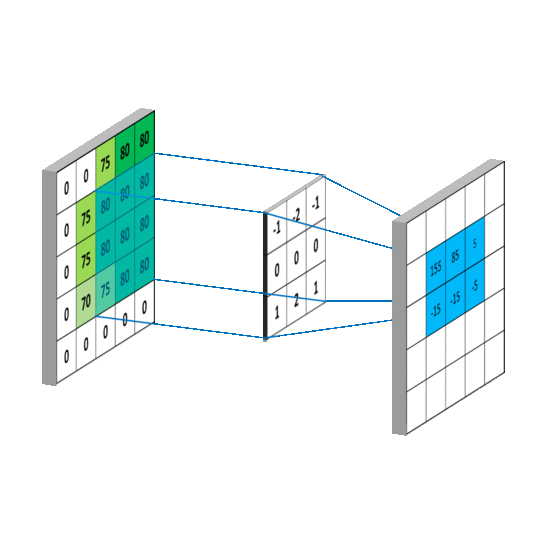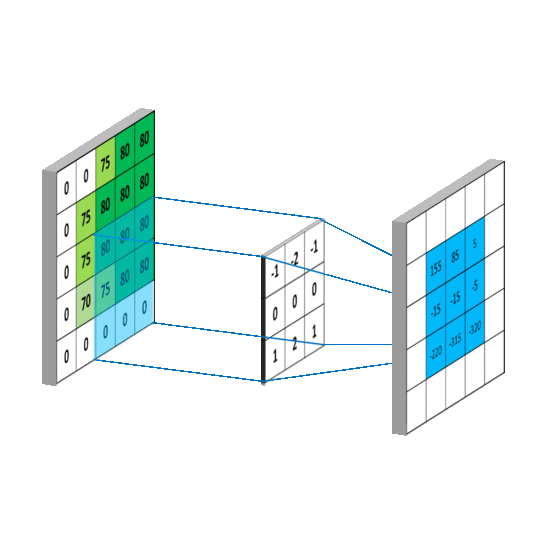
回忆我们神经网络的知识，我们的构造函数中w，是不是和这里的卷积核惊人相似！而每个卷积核中都具有一些列参数，我们需要调整这个识别的参数让我们的特征提取更加顺利，更加倾向于我们的预判结果（训练）。

换句话说，神经网络中的全联接参数优化，不变成了一个个卷积核的参数了，我们需要优化的参数大幅度减少！

CNN最大的利用了图像的局部信息。图像中有固有的局部模式（比如轮廓、边界，人的眼睛、鼻子、嘴等）可以利用，显然应该将图像处理中的概念和神经网络技术相结合，对于CNN来说，并不是所有上下层神经元都能直接相连，而是通过“卷积核”作为中介。
同一个卷积核在所有图像内是共享的，图像通过卷积操作后仍然保留原先的位置关系。卷积神经网络隐含层，通过一个例子简单说明卷积神经网络的结构。假设m-1=1是输入层，我们需要识别一幅彩色图像，这幅图像具有四个通道ARGB（透明度和红绿蓝，对应了四幅相同大小的图像），假设卷积核大小为100100，共使用100个卷积核w1到w100（从直觉来看，每个卷积核应该学习到不同的结构特征）。
用w1在ARGB图像上进行卷积操作，可以得到隐含层的第一幅图像；这幅隐含层图像左上角第一个像素是四幅输入图像左上角100100区域内像素的加权求和，以此类推。
同理，算上其他卷积核，隐含层对应100幅“图像”。每幅图像对是对原始图像中不同特征的响应。按照这样的结构继续传递下去。
CNN中还有max-pooling等操作进一步提高鲁棒性。

综上，我们就是通过训练，要得到一个合理的卷积核是我们的目的（参数共享），优化器我们还是选择梯度下降算法即可

参数共享是指在一个模型的多个函数中使用相同的参数，它是卷积运算带来的固有属性。

在全连接中，计算每层的输出时，权重矩阵中的元素只作用于某一个输入元素一次；

而在卷积神经网络中，卷积核中的每一个元素将作用于每一个局部输入的特定位置上。根据参数共享的思想，我们只需要学习一组参数集合，而不需要针对每一个位置的每一个参数来进行优化学习，从而大大降低了模型的存储需求。

卷积神经网络

卷积神经网络（Convolutional Neural Networks, CNN）是一类包含卷积计算且具有深度结构的前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一 。由于卷积神经网络能够进行平移不变分类（shift-invariant classification），因此也被称为“平移不变人工神经网络（Shift-Invariant Artificial Neural Networks, SIANN）” 。
《百度百科》

典型的卷积神经网络由3部分构成：

• 卷积层
• 池化层
• 全连接层

卷积层负责提取图像中的局部特征；池化层用来大幅降低参数量级(降维)；全连接层类似传统神经网络的部分，用来输出想要的结果。
那么只要满足上面的条件，网络搭建起来就可以用【优化器】去迭代就好啦～

本文中将手把手带你实现一个超超超简单的LENET-5卷积神经网络：
模型为： 输入 - 第一层卷积 - 第一层池化 - 第二层卷积 - 第二层池化 - 第三层卷积 - 第一层全连接 - Drop层 - 第二层全连接输出

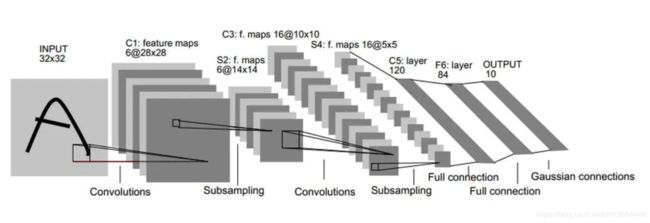
LeNet-5共有7层，不包含输入，每层都包含可训练参数；每个层有多个Feature Map，每个FeatureMap通过一种卷积滤波器提取输入的一种特征，然后每个FeatureMap有多个神经元。
想要了解具体结构可以点击，LeNet-5结构讲解来查看。
学习的还是我们之前的mnist训练集。

代码实现

选择架构：tensorflow会使我们的工作变得简单很多。
我们首先理清思路：我们需要构建模型，之后训练模型并将训练好的神经网络保存下来。然后就可以调用我们的网络来执行自己的识别操作。

1. 建立模型-训练模型-保存模型
2. 使用模型测试

首先我们来构建模型函数：

#!/usr/bin/python
# -*- coding: utf-8 -*

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import tensorflow as tf

FLAGS = None


def deepnn(x):

  with tf.name_scope('reshape'):
    x_image = tf.reshape(x, [-1, 28, 28, 1])

  #第一层卷积层，卷积核为5*5，生成6个feature maps.
  with tf.name_scope('conv1'):
    W_conv1 = weight_variable([5, 5, 1, 6])
    b_conv1 = bias_variable([6])
    h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1) #激活函数采用relu

  # 第一层池化层，下采样2.
  with tf.name_scope('pool1'):
    h_pool1 = max_pool_2x2(h_conv1)

  # 第二层卷积层，卷积核为5*5，生成16个feature maps
  with tf.name_scope('conv2'):
    W_conv2 = weight_variable([5, 5, 6, 16])
    b_conv2 = bias_variable([16])
    h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)#激活函数采用relu

  # 第二层池化层，下采样2.
  with tf.name_scope('pool2'):
    h_pool2 = max_pool_2x2(h_conv2)

  with tf.name_scope('conv3'):
    W_conv3 = weight_variable([5, 5, 16, 120])
    b_conv3 = bias_variable([120])
    h_conv3 = tf.nn.relu(conv2d(h_pool2, W_conv3) + b_conv3)#激活函数采用relu

  # #第一层全连接层，将7x7x16个feature maps与120个features全连接
  # with tf.name_scope('fc1'):
  #     W_fc1 = weight_variable([7 * 7 * 16, 120])
  #     b_fc1 = bias_variable([120])
  #
  #     h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*16])
  #     h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

  # 第二层全连接层，将120个7 * 7 * feature maps与84个features全连接
  with tf.name_scope('fc2'):
      W_fc2 = weight_variable([7 * 7 * 120, 84])
      b_fc2 = bias_variable([84])

      h_pool3_flat = tf.reshape(h_conv3, [-1, 7 * 7 * 120])
      h_fc2 = tf.nn.relu(tf.matmul(h_pool3_flat, W_fc2) + b_fc2)

  #dropout层，训练时候随机让一半的隐含层节点权重不工作，防止过拟合
  with tf.name_scope('dropout'):
    keep_prob = tf.placeholder(tf.float32)
    h_fc1_drop = tf.nn.dropout(h_fc2, keep_prob)

  # 第三层全连接层，84个features和10个features全连接
  with tf.name_scope('fc3'):
    W_fc3 = weight_variable([84, 10])
    b_fc3 = bias_variable([10])

    y_conv = tf.matmul(h_fc1_drop, W_fc3) + b_fc3
  return y_conv, keep_prob

#卷积
def conv2d(x, W):
  return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')

#池化
def max_pool_2x2(x):
  return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],
                        strides=[1, 2, 2, 1], padding='SAME')
#权重
def weight_variable(shape):
  initial = tf.truncated_normal(shape, stddev=0.1)
  return tf.Variable(initial)

#偏置
def bias_variable(shape):
  initial = tf.constant(0.1, shape=shape)
  return tf.Variable(initial)

上面的代码就是把哥哥层都链接好了即可，不熟悉的也是你tensorflow不熟悉罢了。
之后构建训练主函数：

1. 导入数据
2. 初始化输入输出
3. 构建网络模型
4. 构建损失函数
5. 构建优化器
6. 初始化训练场，并开启记录
7. 开始训练，记录模型
8. 保存，记录地址并打印

另外，我们引入accuracy来记录准确率的记录与运算，运算方法是利用包中的测试集

#!/train_minist_model.py
# -*- coding: utf-8 -*

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse
import sys
import tempfile

from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt
import tensorflow as tf

import mnist_model

FLAGS = None


def main(_):
    mnist = input_data.read_data_sets(FLAGS.data_dir, one_hot=True)

    #输入变量，mnist图片大小为28*28
    x = tf.placeholder(tf.float32, [None, 784])

    #输出变量，数字是1-10
    y_ = tf.placeholder(tf.float32, [None, 10])

    # 构建网络，输入—>第一层卷积—>第一层池化—>第二层卷积—>第二层池化—>第一层全连接—>第二层全连接
    y_conv, keep_prob = mnist_model.deepnn(x)

    #第一步对网络最后一层的输出做一个softmax，第二步将softmax输出和实际样本做一个交叉熵
    #cross_entropy返回的是向量
    with tf.name_scope('loss'):
      cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_,
                                                              logits=y_conv)

    #求cross_entropy向量的平均值得到交叉熵
    cross_entropy = tf.reduce_mean(cross_entropy)
    #AdamOptimizer是Adam优化算法：一个寻找全局最优点的优化算法，引入二次方梯度校验
    with tf.name_scope('adam_optimizer'):
      train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

    #记录在测试集上的精确度
    with tf.name_scope('accuracy'):
      correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1)) #测试集判断
      correct_prediction = tf.cast(correct_prediction, tf.float32) #数据准换
    accuracy = tf.reduce_mean(correct_prediction) #均值代表准确率

    #将训练的网络保存下来
    saver = tf.train.Saver() #初始化

    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        writer = tf.summary.FileWriter("./log/", sess.graph) #记录器开始
        cost_accum2 = []
        for i in range(1000):
            batch = mnist.train.next_batch(50)
            if i % 10 == 0:
                train_accuracy = accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0})#输入是字典，表示tensorflow被feed的值
                print('step %d, training accuracy %g' % (i, train_accuracy))
                cost_accum2.append(train_accuracy)  # 记录准确率
            train_step.run(feed_dict={x: batch[0], y_: batch[1], keep_prob: 0.5})

        test_accuracy = 0
        for i in range(200):
          batch = mnist.test.next_batch(50)
          test_accuracy += accuracy.eval(feed_dict={x: batch[0], y_: batch[1], keep_prob: 1.0}) / 200;

        print('test accuracy %g' % test_accuracy)

        save_path = saver.save(sess,"mnist_cnn_model.ckpt") #保存路径g
        print('save_path : ',save_path)
        writer.close() #  关闭记录器

        draw(cost_accum2)

#绘制
def draw(cost_accum2):
    #plt.plot(range(len(cost_accum)), cost_accum, 'r')
    plt.plot(range(len(cost_accum2)), cost_accum2, 'b')
    plt.title('Accuracy of myCNN')
    plt.xlabel('step/10')
    plt.ylabel('accuracy')
    print('show')
    plt.show()
    
if __name__ == '__main__':
    parser = argparse.ArgumentParser()
    parser.add_argument('--data_dir', type=str,
                        default='./',
                        help='Directory for storing input data')
    FLAGS, unparsed = parser.parse_known_args()
    tf.app.run(main=main, argv=[sys.argv[0]] + unparsed)

这一步我们就完成了我们训练与保存！我们的准确率曲线绘制如下：

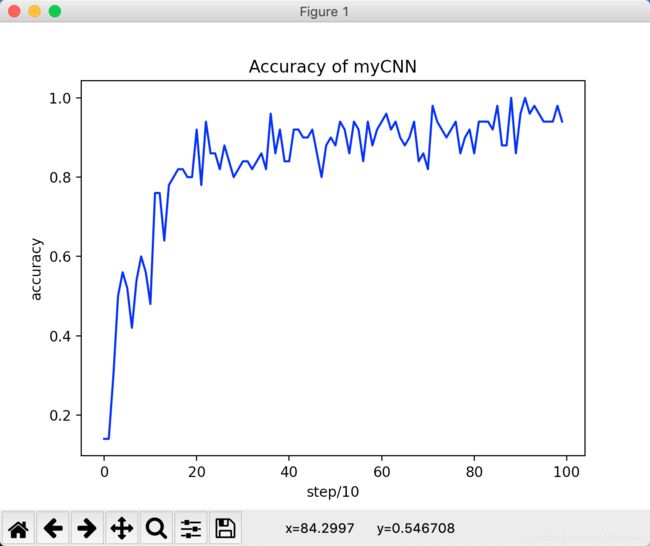
可以看出虽然训练了1000次，但是还是有潜力可以挖掘的！此时的准确率已达到0.9342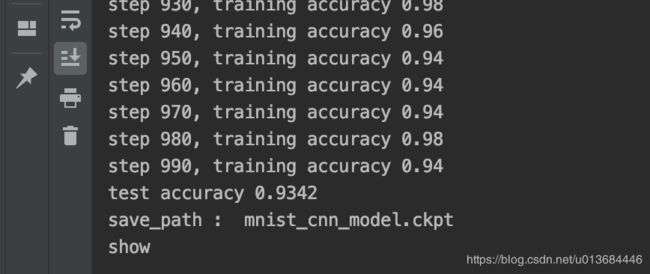
那么我们怎么使用我们保存的模型呢？这个说实话不是学习重点，保存代码，直接用就行了‍♂️

#!/usr/bin/python
# -*- coding: utf-8 -*

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function


import tensorflow as tf

import mnist_model
from PIL import Image, ImageFilter

def load_data(argv):

    grayimage = Image.open(argv).convert('L')
    width = float(grayimage.size[0])
    height = float(grayimage.size[1])
    newImage = Image.new('L', (28, 28), (255))

    if width > height:
        nheight = int(round((20.0/width*height),0))
        if (nheigth == 0):
            nheigth = 1
        img = grayimage.resize((20,nheight), Image.ANTIALIAS).filter(ImageFilter.SHARPEN)
        wtop = int(round(((28 - nheight)/2),0))
        newImage.paste(img, (4, wtop))
    else:
        nwidth = int(round((20.0/height*width),0))
        if (nwidth == 0):
            nwidth = 1
        img = grayimage.resize((nwidth,20), Image.ANTIALIAS).filter(ImageFilter.SHARPEN)
        wleft = int(round(((28 - nwidth)/2),0))
        newImage.paste(img, (wleft, 4))

    tv = list(newImage.getdata())
    tva = [ (255-x)*1.0/255.0 for x in tv]
    return tva

def main(argv):

    imvalue = load_data(argv)

    x = tf.placeholder(tf.float32, [None, 784])
    y_ = tf.placeholder(tf.float32, [None, 10])
    y_conv, keep_prob = mnist_model.deepnn(x)

    y_predict = tf.nn.softmax(y_conv)
    init_op = tf.global_variables_initializer()
    saver = tf.train.Saver()
    with tf.Session() as sess:
        sess.run(init_op)
        saver.restore(sess, "mnist_cnn_model.ckpt")
        prediction=tf.argmax(y_predict,1)
        predint = prediction.eval(feed_dict={x: [imvalue],keep_prob: 1.0}, session=sess)
        print (predint[0])

if __name__ == "__main__":
    # main(sys.argv[1])
    main('4_my.png')

好了，到此我们卷积神经网络的入门就结束了，下面我们要学习的是RNN结构。
而你在卷积上的优化更多是针对你拥有的数据集，来优化你的模型结构，注意鲁棒性的优化和避免过度拟合。