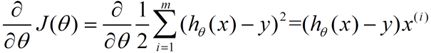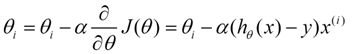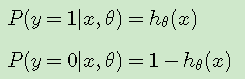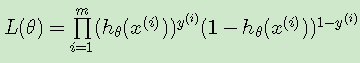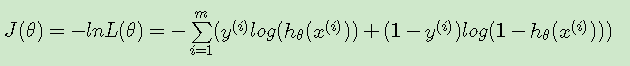机器学习面试知识点总结第二弹
生成模型与判别模型
监督学习模型可分为生成模型与判别模型
- 判别模型直接学习决策函数或者条件概率分布
- 直观来说，判别模型学习的是类别之间的最优分隔面，反映的是不同类数据之间的差异
- 生成模型学习的是联合概率分布
P(X,Y)，然后根据条件概率公式计算P(Y|X) - 判别模型
- K 近邻、感知机（神经网络）、决策树、逻辑斯蒂回归、最大熵模型、SVM、提升方法、条件随机场
- 生成模型
- 朴素贝叶斯、隐马尔可夫模型、混合高斯模型、贝叶斯网络、马尔可夫随机场
梯度下降法
梯度下降法（Gradient descent）是一个最优化算法，它的作用是找到一个函数的局部最小值。它是最小化损失函数的一种方法。
h(x)是要拟合的函数，J(theta)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数，j是参数的个数。
我们程序也需要一个机制去评估我们θ是否比较好，所以说需要对我们做出的h函数进行评估，一般这个进行评估的函数称为损失函数（loss function），描述h函数不好的程度，这里我们称这个函数为J函数。
梯度下降法的算法流程如下：
1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。
2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。
具体操作：
下面是更新的过程，也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。
随机梯度下降SGD (stochastic gradient descent)
梯度下降算法在每次更新回归系数的时候都需要遍历整个数据集（计算整个数据集的回归误差），该方法对小数据集尚可。但当遇到有数十亿样本和成千上万的特征时，就有点力不从心了，它的计算复杂度太高。改进的方法是一次仅用一个样本点（的回归误差）来更新回归系数。这个方法叫随机梯度下降算法。
小批量梯度下降法(Mini-Batch Gradient Descent)
批量梯度下降法一定能沿着极小值的方向迈进，比较稳定，然而每次计算梯度时都需要遍历所有样本，计算量比较大。
随机梯度下降法的运算速度虽然比较快，但有可能跳出局部最优解，每次的迈进方向不稳定，甚至有可能向反方向迈进。
故每次计算梯度时，选取一部分样本，即小批量梯度下降法。与随机梯度下降法相比，增强了方向的稳定性。与批量梯度下降法相比，运算量大大减少，运行速度也更快。
牛顿法和梯度下降法有什么不同？
牛顿法（Newton's method）：使用函数f（x）的泰勒级数的前面几项来寻找方程f（x） = 0的根。特点：收敛速度很快。
如何绘制ROC曲线，AOC的物理意义
ROC（Receiver Operating Characteristic）曲线全称是“受试者工作特征”，通常用来衡量一个二分类学习器的好坏。如果一个学习器的ROC曲线能将另一个学习器的ROC曲线完全包住，则说明该学习器的性能优于另一个学习器。
1. 混淆矩阵，一个在评判二分类学习器的时候通常都会用到的表格
| 预测值 | 预测值 | |
|---|---|---|
| 实际值 | 真 | 假 |
| 真 | TP | FN |
| 假 | FP | TN |
2. FPR和TPR
FPR（False Positive Rate）和TPR（True Positive Rate）分别对应着ROC曲线的横纵坐标，其定义如下
于一个学习器它的预测结果只能产生一对（FPR，TPR），这只能绘制一个点，不足以绘制出一条曲线。实际上对于许多学习器在判定二分类问题时是预测出一个对于真值的范围在[0.0, 1.0]之间的概率值，而判定是否为真值则看该概率值是否大于设定的阈值（Threshold）。例如如果阈值设定为0.5则所有概率值大于0.5的均为正例，其余为反例。因此对于不同的阈值我们可以得到一系列相应的FPR和TPR，从而绘制出ROC曲线。
以下列数据举例：
y_true = [0, 1, 0, 1]，真实值
y_score = [0.1, 0.35, 0.4, 0.8]， 预测概率值
分别取4组判定正例用的阈值：[0.1, 0.35, 0.4, 0.8]，可得相应4组FPR,TPR:
FPR: [1, 0.5, 0.5, 0]
TPR: [1, 1, 0.5, 0.5]
绘制ROC曲线图如下： 
ROC曲线所覆盖的面积称为AUC（Area Under Curve），可以更直观的判断学习器的性能，AUC越大则性能越好。对于该例的AUC值为0.75。
类别不均衡问题
基础概念
类别不均衡是指在分类学习算法中，不同类别样本的比例相差悬殊，它会对算法的学习过程造成重大的干扰。比如在一个二分类的问题上，有1000个样本，其中5个正样本，995个负样本，在这种情况下，算法只需将所有的样本预测为负样本，那么它的精度也可以达到99.5%，虽然结果的精度很高，但它依然没有价值，因为这样的学习算法不能预测出正样本。
解决方法
1、欠采样，减少数量较多那一类样本的数量，使得正负样本比例均衡。
2、过采样，增加数量较少那一类样本的数量，使得正负样本比例均衡。
3、不处理样本，样本分类阈值移动。
常见的损失函数？
Logistics 回归 逻辑回归原理
What
逻辑回归是一个有监督学习的分类算法，它可以处理二元分类以及多元分类。虽然它名字里面有“回归”两个字，却不是一个回归算法。
假设函数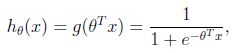
二元逻辑回归的损失函数
假设我们的样本输出是0或者1两类。那么我们有：
设定一个阈值0.5
从而，当我们要判别一个新来的特征属于哪个类时，只需求即可，若大于0.5就是y=1的类，反之属于y=0类。
模型的数学形式确定后，剩下就是如何去求解模型中的参数。统计学中常用的一种方法是最大似然估计，即找到一组参数，使得在这组参数下，我们的数据的似然度（概率）越大。在逻辑回归模型中，似然度可表示为：得到了y的概率分布函数表达式，我们就可以用似然函数最大化来求解我们需要的模型系数θ。
为了方便求解，这里我们用对数似然函数最大化，对数似然函数取反即为我们的损失函数J(θ)。其中：
似然函数的代数表达式为：
其中m为样本的个数。
对似然函数对数化取反的表达式，即损失函数表达式为：
内容来源:https://www.cnblogs.com/pinard/p/6029432.html
K近邻算法
基本思想
如果一个实例在特征空间中的K个最相似（即特征空间中最近邻）的实例中的大多数属于某一个类别，则该实例也属于这个类别。所选择的邻居都是已经正确分类的实例。
该算法假定所有的实例对应于N维欧式空间Ân中的点。通过计算一个点与其他所有点之间的距离，取出与该点最近的K个点，然后统计这K个点里面所属分类比例最大的，则这个点属于该分类。
如果K=3，绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类。
如果K=5，绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形，还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类。
KNN中的K如何选取的？
在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。
KNN最近邻分类算法的过程？
1. 计算测试样本和训练样本中每个样本点的距离（常见的距离度量有欧式距离，马氏距离等）；
2. 对上面所有的距离值进行排序；
3. 选前 k 个最小距离的样本；
4. 根据这 k 个样本的标签进行投票，得到最后的分类类别；K-means算法原理
聚类（Clustering）是一种无监督学习(unsupervised learning)，简单地说就是把相似的对象归到同一簇中。簇内的对象越相似，聚类的效果越好。
K-均值（K-means）聚类算法
聚类分析（cluster analysis）试图将相似对象归入同一簇，将不相似对象归到不同簇。
算法基本思想
在数据集中根据一定策略选择K个点作为每个簇的初始中心，然后观察剩余的数据，将数据划分到距离这K个点最近的簇中，也就是说将数据划分成K个簇完成一次划分，但形成的新簇并不一定是最好的划分，因此生成的新簇中，重新计算每个簇的中心点，然后在重新进行划分，直到每次划分的结果保持不变。
KMeans算法的基本思想是初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心，从而确定新的簇心。一直迭代，直到簇心的移动距离小于某个给定的值。
K-Means聚类算法主要分为三个步骤：
(1)第一步是为待聚类的点寻找聚类中心；
(2)第二步是计算每个点到聚类中心的距离，将每个点聚类到离该点最近的聚类中去；
(3)第三步是计算每个聚类中所有点的坐标平均值，并将这个平均值作为新的聚类中心；
反复执行(2)、(3)，直到聚类中心不再进行大范围移动或者聚类次数达到要求为止。
数据预处理
1. 缺失值，填充缺失值fillna： i. 离散：None, ii. 连续：均值。 iii. 缺失值太多，则直接去除该列
2. 连续值：离散化。有的模型（如决策树）需要离散值
3. 对定量特征二值化。核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0。如图像操作
4. 皮尔逊相关系数，去除高度相关的列