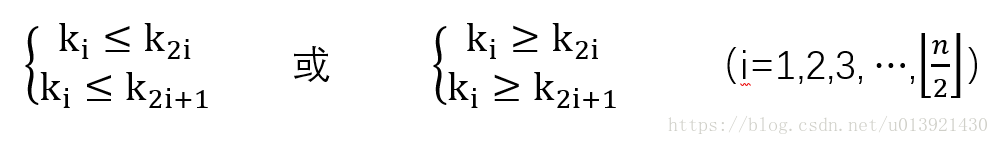【数据结构、算法】八大排序算法概述（算法复杂度、稳定性）

前言

  排序是计算机程序设计中一个非常重要的操作，它将一个数据元素（或记录）的任意序列重新排列成一个按关键字有序的序列。在有序的序列中查找元素的效率很高，（例如，折半查找法的平均查找长度为 log2(n+1)−1 l o g 2 ( n + 1 ) − 1 ），但是无序序列只能逐一查找，其平均查找长度为 (n+1)/2 ( n + 1 ) / 2 。又比如构建二叉排序树的过程，就是一个排序的过程，因此，如何进行排序，尤其是高效排序，是一个重要的课题。
  排序的数据元素是很多样的，其关键字也是多种的，为了方便理解和表示，后面均使用数列进行分析，其用于排序的关键字就是数字本身。（默认将序列排列成升序）

稳定性

  假设某一序列的关键字是Ki  (i=1,2,3,⋯⋯,n) ( i = 1 , 2 , 3 , ⋯ ⋯ , n ) ，且存在Km=Ks  (1≤m<s≤n) ( 1 ≤ m < s ≤ n ) ，如果进过排序后，Km依然在Ks左侧（前方），则称该排序方法是稳定的。反之，若Km排列在Ks右侧（后方），则称该排序方法是不稳定的。

内部排序与外部排序

  由于排序的记录数量的不同，使排序过程中设计的存储器不同，可以将排序分为两类，第一类是内部排序，指的是待排序记录存放在计算机自身的存储器中进行排序的过程；另一类是外部排序，指的是由于待排序记录数量很大，以致于内存无法一次全部容纳所有记录，在排序过程中需要从外存中访问记录的排序过程。
在本篇博文中主要分析的都是常见的内部排序算法，将会尽力用简短易于理解的语言来分析。

---

为了方便叙述，首先给出一个无序序列，后续的算法分析都是基于这个序列。序列如下

---

排序算法

直接插入排序

  直接插入排序（Straight Insertion Sort）是一种非常简单易理解的排序方法，它的操作是将一个记录插入到已经排序号好的有序表中。假设上面的序列中，前四个元素经过排序后已经有序，序列为38,49,65,97，再插入76。假设从右往左进行对比，因为65<76<97，所以76被插入到65与97之间。依次对每个元素进行这样的操作，直到所有的元素都被插入到有序表中。
  在最好的情况下，序列已经是有序的，每次插入元素只需要与有序表中最后一个元素进行比较，时间复杂度为 O(n) O ( n ) 。在最坏的情况下，每次插入元素需要与前面所有的元素进行比较，时间复杂度为 O(n2) O ( n 2 ) ，平均时间复杂度为 O(n2) O ( n 2 ) ，算法的空间复杂度为 O(1) O ( 1 ) 。可以想象，在插入第二个49时，当它与前方的49进行比较，两者相等，不会把第二个放在第一个的前方，所以直接插入排序是稳定的。

简单选择排序

  简单选择排序（Simple Select Sort，也称为“选择排序”或者是“直接选择排序”），其方法是：找出序列中的最小关键字，然后将这个元素与序列首端元素交换位置。例如，序列前i个元素已经有序，从第i+1到第n个元素中选择关键字最小的元素，假设第j个元素为最小元素，则交换第j个元素与第i+1个元素的位置。依次执行此操作，直到第n-1个元素也被确定。

  相比于上面提到的两种排序方法，简单选择排序不论是否序列已经有序都需要进行n-1次最小数选择，所以它的最好、最坏以及平均时间复杂度都是 O(n2) O ( n 2 ) 。算法的空间复杂度为 O(1) O ( 1 ) 。此外，由于交换位置的两个元素的位置是跳跃的，所以相同关键字的元素位置可能发生交换。例如在上面的序列中，第二个49后面还有一个元素1，那么在第一次排序后，两个49的排列顺序就发生了改变，因此简单选择排序是 不稳定的。

希尔排序

  希尔排序（Shell Sort，又称“缩小量排序”），它也是一种插入排序，但是在时间效率上有了很大的改进。它的基本思想是：假设序列中有n个元素，首先选择一个间隔gap，将全部的序列分为gap个子序列，然后分别在子序列内部进行简单插入排序，得到一个新的主序列；而后缩小gap，再得到子序列，对子序列进行简单插入排序，又再次得到新的主序列，直到gap=1为止。在算法中，排序前期，由于gap值比较大，每个子序列中元素少，排序快，到了排序后期，由于前面的排序导致序列已经基本有序，排序速度也很快。
  希尔排序的时间复杂度与gap的选择有很大的关系，一般时间复杂度是低于 O(n2) O ( n 2 ) 。算法的空间复杂度为 O(1) O ( 1 ) 。由于希尔排序中元素交换位置也是跳跃式的，所以它也是不稳定的。

冒泡排序

  冒泡排序（Bubble Sort）也是一种简单的排序算法，其方法是：首先将第一个关键字与第二个关键字进行比较，若逆序，则交换位置；然后比较第二个与第三个关键字，依次进行比较，直到第n-1个关键字和第n的关键字完成比较为止。上述过程是第一趟冒泡，结果就是值最大的关键字排在了最后面。然后对前n-1个关键字进行第二趟冒泡，如此往复，直到整个序列有序为止。很明显，若果某一趟冒泡过程中没有发生元素位置交换，那么此时整个序列已经是有序的，无需继续下面的操作。
  在最好的情况下，序列已经是有序的，只进行了第一趟冒泡比较，此时算法的时间复杂度为 O(n) O ( n ) 。在最坏的情况下，执行了n-1次冒泡，时间复杂度为 O(n2) O ( n 2 ) 。算法的空间复杂度为 O(1) O ( 1 ) 。在比较上面序列中的第一个49与第二个49时，两者相等，不会进行位置交换，所以算法是稳定的。

快速排序

  快速排序（Quick Sort），快速排序是对冒泡排序的一种改进，它的基本思想如下：通过一趟排序将序列分割成两部分，其中一部分的关键字均大于另一部分，则可以分别对两部分进行排序，从而使整个序列有序。
  实施方案是：首先选择一个关键字作为枢纽（通常为第一个元素的关键字），然后让所有关键字比枢纽小元素放在枢纽前面，比枢纽大的元素放在枢纽后面。这样就根据枢纽最后落在的位置将序列分割成为了两部分。然后进行递归运算，就可以对数列进行排序。
  例如用快速排序上面的序列。起初以49为枢纽，用两个指针分别指向第0个和最后一个元素（i=0，j=7）。从后往前搜索，搜索至27时（i=0，j=6），由于27<49，交换两个元素的位置，序列变成27、38、65、97、76、13、49、49，这时（i=0,j=6）；从前往后搜索，搜索i=2时，65>49，则交换元素的位置，序列变成27、38、49、97、76、13、65、49，此时（i=2,j=6）；再从后往前搜索，搜索至j=5时，13<49, 则交换元素的位置，序列变成27、38、13、97、76、49、65、49，此时（i=3,j=5），从前往后搜索，搜索至i=4时，97>49，交换元素的位置，序列变成27、38、13、49、76、97、65、49，此时（i=4,j=5），再从后往前搜索，由于i=j=4时不会发生交换，所以第一趟搜索结束，此时以49为分界，49前方的数字均大于49后方的数字。然后分别对49的左右两部分进行递归排序。
  快速排序算法递归的次数取决于元素的数目，最理想的情况下，每次划分左右两部分的长度相等，则需要递归次 (nlogn) ( n l o g n ) 次，每次需要比较定位的次数为n，所以最理想的时间复杂度为 O(nlogn) O ( n l o g n ) 。可以证明平均时间复杂度也为 O(nlogn) O ( n l o g n ) ，最坏的情况下它可以被看做冒泡排序，时间复杂度为 O(n2) O ( n 2 ) 。空间复杂度是递归过程中的需要占据的空间，最优情况下空间复杂度为 O(nlogn) O ( n l o g n ) ，很明显它是不稳定的。

堆排序

  对于有n个元素的关键字序列 k1,k2,k3,⋯⋯,kn k 1 , k 2 , k 3 , ⋯ ⋯ , k n ，当且仅当所有关键字满足以下条件时称之为最小堆或者最大堆。

  前者称之为最小堆，后者称之为最大堆。前者任一节点的关键之均小于其左右孩子的关键字，后者任一节点的关键之均大于其左右孩子的关键字，下面以小堆为例进行讲解。
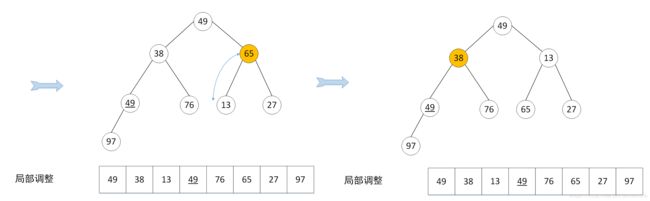
  首先根据上面的数列的关键字构建一个堆，然后找到从下往上的第一个非叶子结点97，对比其与其左右孩子的大小，若有孩子比起小则交换位置。

  然后找到下一个非叶子结点，对比其叶子结点，进行位置交换，这里将65与13交换位置。

  依次对比，直到形成最小堆，此时堆顶为13，输出13，或者将第一位数与最后一位数交换位置。

  如此往复，直到输出所有元素为止。

  堆排序的时间复杂度为 O(nlogn) O ( n l o g n ) ，需要一个临时空间用于交换元素，所以空间复杂度为 O(1) O ( 1 ) ，堆排序的位置交换也是跳跃式的，是一个不稳定的排序方法。

基数排序

  基数排序的思想是按照组成关键字的各个数位进行排序，它是分配排序的一种。假如关键字是十进制数字，那么令r=10，d是所有关键字中的最大位数（位数小于d的数字，在前方补0）。基数排序可以从最低有效位开始，也可以从最高有效位开始。
  基数排序的思想是：设立r个队列，编号分别为0,1,2,3…,r-1。首先按照最低有效位的值，将n个关键字放置到r个队列中，然后从小到大将元素收集起来，再按照次低位的值将元素放置到各个队列中，再进行收集，重复上述过程，直到收集完毕为止。

  对于有n个元素的序列，执行一次放置和收集的时间为 O(n+r) O ( n + r ) ,则其时间复杂度为
O(d(n+r)) O ( d ( n + r ) ) ,空间复杂度为 O(dr) O ( d r ) ，虽然基数排序的位置交换是跳跃的，但是元素放置和收集时都是按照顺序进行的，所以不会打乱顺序，是一种稳定的算法。

归并排序

  之前有写过一篇归并排序的博文，不理解的可以到《【数据结构】二叉树的遍历及应用(https://blog.csdn.net/u013921430/article/details/80252035)》去阅读，讲解的很详细。归并排序的时间复杂度为 O(nlogn) O ( n l o g n ) ，空间复杂度为 O(n) O ( n ) ，是一种稳定的排序算法。

总结

  各个算法的时间复杂度、空间复杂度及稳定性的表格如上图所示（偷个懒，找了本数，把书上的内容拍下来了。）。迄今为止，已有的排序方法远远不止上面的八种，各个方法都有自己的优缺点。选择排序算法时需要考虑很多因素，比如：
  （1）待排序的记录个数；
  （2）记录本身的大小；
  （3）对稳定性的要求；
  （4）关键字的分布；
  （5）语言工具的条件，辅助空间的大小。
依据这几点因素可以得出以下结论：
  （1）当待排序的记录数目n比较小时，可以采用直接插入排序和选择排序
  （2）当记录中的关键字基本有序时，宜采用直接插入排序或者冒泡排序。
  （3）当n较大且排序记录关键字最大位数较小是，宜采用基数排序。
  （4）当n较大，则可以选择时间复杂度为 O(nlogn) O ( n l o g n ) 的排序方法：快速排序、堆排序或者归并排序，前两者不是稳定排序，当要求稳定排序时，可以选择归并排序。

  已完。。

参考书籍

《软件设计师教程》 陈平 褚华 主编
《C++与数据结构》 高飞 主编，白霞 胡进等 副主编