MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution
2020CVPR -- Deep Unfolding Network for Image Super-Resolution
[paper] : Deep Unfolding Network for Image Super-Resolution
[github] : https://github.com/cszn/USRNet
Abstract
Learning-based single image super-resolution (SISR) methods are continuously showing superior effectiveness and efficiency over traditional model-based methods, largely due to the end-to-end training. However, different from model-based methods that can handle the SISR problem with different scale factors, blur kernels and noise levels under a unified MAP (maximum a posteriori) framework, learning-based methods generally lack such flexibility.
提出问题:
首先,肯定了深度学习 SISR 方法的优越表现;然后,指出基于深度学习 SISR 的问题,即:
基于模型的(非深度学习的)SISR 方法在同一标准的最大后验概率(maximum a posteriori,MAP)下,可以对不同的尺度因素,模糊内核和噪音水平的 LR 图像进行研究处理;但基于深度学习的 SISR 缺乏这种灵活度。
To address this issue, this paper proposes an end-to-end trainable unfolding network which leverages both learning-based methods and model-based methods. Specifically, by unfolding the MAP inference via a half-quadratic splitting algorithm, a fixed number of iterations consisting of alternately solving a data subproblem and a prior subproblem can be obtained. The two subproblems then can be solved with neural modules, resulting in an end-to-end trainable, iterative network. As a result, the proposed network inherits the flexibility of model-based methods to super-resolve blurry, noisy images for different scale factors via a single model, while maintaining the advantages of learning-based methods.
解决问题的方法:
为了解决这一问题,本文提出了的端到端可训练展开网络,同时利用了基于学习的方法和基于模型的方法。
具体地,通过半二次分裂算法(half-quadratic splitting algorithm)展开 MAP 推理,可以得到由交替求解一个数据子问题和一个先验子问题组成的固定迭代次数。
这两个子问题可以用神经模块来解决,从而形成一个端到端可训练的迭代网络。
因此,该网络继承了基于模型的方法的灵活性,可以通过单一模型对不同尺度因子的模糊、噪声图像进行超分辨,同时保持了基于学习的方法的优点。
Extensive experiments demonstrate the superiority of the proposed deep unfolding network in terms of flexibility, effectiveness and also generalizability.
实验结果。
Introduction
让我们看看,Introduction 讲了一个什么故事。
Single image super-resolution (SISR) refers to the process of recovering the natural and sharp detailed highresolution (HR) counterpart from a low-resolution (LR) image. It is one of the classical ill-posed inverse problems in low-level computer vision and has a wide range of realworld applications, such as enhancing the image visual quality on high-definition displays [42, 53] and improving the performance of other high-level vision tasks [13].
笼统介绍了 SISR 是干嘛的。
Despite decades of studies, SISR still requires further study for academic and industrial purposes [35, 64]. The difficulty is mainly caused by the inconsistency between the simplistic degradation assumption of existing SISR methods and the complex degradations of real images [16]. Actually, for a scale factor of
, the classical (traditional) degradation model of SISR [17, 18, 37] assumes the LR image
is a blurred, decimated, and noisy version of an HR image
. Mathematically, it can be expressed by
, (1)
where ⊗ represents two-dimensional convolution of
with blur kernel
,
denotes the standard s-fold downsampler, i.e., keeping the upper-left pixel for each distinct
patch and discarding the others, and
is usually assumed to be additive, white Gaussian noise (AWGN) specified by standard deviation (or noise level)
[71]. With a clear physical meaning, Eq. (1) can approximate a variety of LR images by setting proper blur kernels, scale factors and noises for an underlying HR images. In particular, Eq. (1) has been extensively studied in model-based methods which solve a combination of a data term and a prior term under the MAP framework.
继续详细介绍 SISR,从数学模型角度:学术研究和工业应用之间的差异,主要是由于现有SISR方法的退化假设过于简单,与真实图像的复杂退化不一致造成的。后面,就是具体介绍这个问题的数学含义。对于给定的HR图像,LR 图像由模糊内核、比例因子(降维比例)和噪声决定。
Eq.(1) 在基于模型的方法中得到了广泛的研究,这种方法解决了MAP框架下数据项和先验项的组合。
在 Eq.(1) 基础上,将引出下一段关于基于模型和基于深度学习 SISR 算法的问题。
Though model-based methods are usually algorithmically interpretable, they typically lack a standard criterion for their evaluation because, apart from the scale factor, Eq. (1) additionally involves a blur kernel and added noise. For convenience, researchers resort to bicubic degradation without consideration of blur kernel and noise level [14,56, 60]. However, bicubic degradation is mathematically complicated [25], which in turn hinders the development of model-based methods.
For this reason, recently proposed SISR solutions are dominated by learning-based methods that learn a mapping function from a bicubicly downsampled LR image to its HR estimation. Indeed, significant progress on improving PSNR [26, 70] and perceptual quality [31, 47, 58] for the bicubic degradation has been achieved by learning-based methods, among which convolutional neural network (CNN) based methods are the most popular, due to their powerful learning capacity and the speed of parallel computing. Nevertheless, little work has been done on applying CNNs to tackle Eq. (1) via a single model. Unlike model-based methods, CNNs usually lack flexibility to super-resolve blurry, noisy LR images for different scale factors via a single end-to-end trained model (see Fig. 1).
Figure 1. While a single degradation model (i.e., Eq. (1)) can result in various LR images for an HR image, with different blur kernels, scale factors and noise, the study of learning a single deep model to invert all such LR images to HR image is still lacking.
问题提出:
目前的 SISR 无非两类,基于模型的(非深度学习)和基于深度学习的。这两类方法都有各自的问题。
基于模型的问题:采用双三次退化而不考虑模糊核和噪声水平[14,56,60]。然而,双三次退化在数学上是复杂的[25],这反过来又阻碍了基于模型的方法的发展。
基于深度学习的:CNNs通常缺乏灵活性,无法通过单一的端到端训练模型,针对不同的尺度因子来实现模糊、含有噪声的 LR 图像的超分辨。
问题指明了工作内容,下一段讲本文的工作了。
In this paper, we propose a deep unfolding super-resolution network (USRNet) to bridge the gap between learning-based methods and model-based methods. On one hand, similar to model-based methods, USRNet can effectively handle the classical degradation model (i.e., Eq. (1)) with different blur kernels, scale factors and noise levels via a single model. On the other hand, similar to learning-based methods, USRNet can be trained in an end-to-end fashion to guarantee effectiveness and efficiency.
To achieve this, we first unfold the model-based energy function via a halfquadratic splitting algorithm. Correspondingly, we can obtain an inference which iteratively alternates between solving two subproblems, one related to a data term and the other to a prior term. We then treat the inference as a deep network, by replacing the solutions to the two subproblems with neural modules.
Since the two subproblems correspond respectively to enforcing degradation consistency knowledge and guaranteeing denoiser prior knowledge, USRNet is well-principled with explicit degradation and prior constraints, which is a distinctive advantage over existing learning-based SISR methods.
It is worth noting that since USRNet involves a hyper-parameter for each subproblem, the network contains an additional module for hyper-parameter generation. Moreover, in order to reduce the number of parameters, all the prior modules share the same architecture and same parameters.
本文工作:
在介绍本文工作时,作者的思路是这样的:
1. 先介绍本文的核心思想:结合基于学习的方法和基于模型的方法。
一方面,与基于模型的方法类似,USRNet 可以有效地处理经典的退化模型(即,式(1)))通过单一模型,具有不同的模糊核、尺度因子和噪声水平。
另一方面,与基于学习的方法类似,USRNet 可以以端到端的方式进行培训,以保证有效性和效率。
2. 核心思想是怎么实现的:
首先,通过半二次分裂算法展开基于模型的能量函数。相应地,可以得到一个推理,它迭代地交替解决两个子问题,一个与数据项有关,另一个与先验项有关。
然后,将推理作为一个深层网络,用神经模块代替这两个子问题的解。
3. 解释提出的网络:
由于这两个子问题分别对应于强化降解一致性知识(enforcing degradation consistency knowledge)和保证去噪器先验知识(guaranteeing denoiser prior knowledge),所以 USRNe t对于显式退化和先验约束是很有原则的,这是与现有的基于学习的SISR 方法的显著优势。
值得注意的是,由于 USRNet 涉及到每个子问题的超参数,因此网络包含一个额外的模块用于生成超参数。
此外,为了减少参数的数量,所有之前的模块共享相同的架构和相同的参数。
(当然,只读到这里呢,完全不懂这几句在说什么,看看正文吧,或许能看明白。)
The main contributions of this work are as follows:
1) An end-to-end trainable unfolding super-resolution network (USRNet) is proposed. USRNet is the first attempt to handle the classical degradation model with different scale factors, blur kernels and noise levels via a single end-to-end trained model.
2) USRNet integrates the flexibility of model-based methods and the advantages of learning-based methods, providing an avenue to bridge the gap between model-based and learning-based methods.
3) USRNet intrinsically imposes a degradation constraint (i.e., the estimated HR image should accord with the degradation process) and a prior constraint (i.e., the estimated HR image should have natural characteristics) on the solution.
4) USRNet performs favorably on LR images with different degradation settings, showing great potential for practical applications.
本文的主要贡献:(不厚道地直接翻译了)
1) 提出了一种端到端可训练展开超分辨率网络 (USRNet)。USRNet 是第一个尝试处理经典退化模型与不同的尺度因子,模糊内核和噪声水平通过一个单一的端到端训练模型。
2) USRNet 融合了基于模型方法的灵活性和基于学习方法的优点,为弥合基于模型方法和基于学习方法之间的鸿沟提供了途径。
3) USRNet 本质上强加了一个退化约束(即,估计的 HR 图像应符合退化过程) 和一个先验约束 (即,估计的 HR 图像应该具有自然特征) 上的解决方案。
4) USRNet 在不同退化设置的 LR 图像上表现良好,显示出巨大的实际应用潜力。
Related work
略
Method
Degradation model: classical vs. bicubic
Since bicubic degradation is well-studied, it is interesting to investigate its relationship to the classical degradation model. Actually, the bicubic degradation can be approximated by setting a proper blur kernel in Eq. (1). To achieve this, we adopt the data-driven method to solve the following kernel estimation problem by minimizing the reconstruction error over a large HR/bicubic-LR pairs
(2)
Fig. 2 shows the approximated bicubic kernels for scale factors 2, 3 and 4. It should be noted that since the downsamlping operation selects the upper-left pixel for each distinct s × s patch, the bicubic kernels for scale factors 2, 3 and 4 have a center shift of 0.5, 1 and 1.5 pixels to the upper-left direction, respectively.
由于双三次降解已经得到了很好的研究,因此研究其与经典降解模型的关系是很有趣的。实际上,可以通过在式 (1) 中设置合适的模糊核来近似双三次退化。为了实现这一点,采用数据驱动的方法来解决下面的核估计问题,即在一个较大的 HR/ bicubicr - LR 对 ![]() 上最小化重构误差
上最小化重构误差
![]() (2)
(2)
图2显示了比例因子2、3和4的近似双三次核。需要注意的是,由于 downsamlping 操作为每个不同的 ![]() patch 选择左上角像素,因此比例因子2、3和4的双三次核分别向左上角偏移 0.5、1和1.5像素。
patch 选择左上角像素,因此比例因子2、3和4的双三次核分别向左上角偏移 0.5、1和1.5像素。
Figure 2. Approximated bicubic kernels for scale factors 2, 3 and 4 under the classical SISR degradation model assumption. Note that these kernels contain negative values.
Unfolding optimization
According to the MAP framework, the HR image could be estimated by minimizing the following energy function
where
is the data term,
is the prior term, and
is a trade-off parameter.
给出了 MAP 框架。
In order to obtain an unfolding inference for Eq. (3), the half-quadratic splitting (HQS) algorithm is selected due to its simplicity and fast convergence in many applications. HQS tackles Eq. (3) by introducing an auxiliary variable
, leading to the following approximate equivalence
where
is the penalty parameter.
给出了 HQS 算法处理 MAP 的形式。(对 HQS 完全不了解哦,有点像是,把第一项的 x 换成 z,再加入一个 L2(x, z) 的惩罚项,让 z 与 x 尽可能相似。)
Such problem can be addressed by iteratively solving subproblems for
and
According to Eq. (5),
should be large enough so that
and
are approximately equal to the fixed point. However, this would also result in slow convergence. Therefore, a good rule of thumb is to iteratively increase
. For convenience, the
in the
-th iteration is denoted by
.
给出了具体解公式 (4)的方法,即把(4)拆分从两部分(5)和(6)。(5)用来解 ![]() 。(6)用来解
。(6)用来解 ![]() 。
。
其中,![]() 应该足够大,使得和近似等于不动点。然而,这也会导致缓慢的收敛。因此,一个好的经验法则是迭代递增
应该足够大,使得和近似等于不动点。然而,这也会导致缓慢的收敛。因此,一个好的经验法则是迭代递增 ![]() 。为方便起见,第
。为方便起见,第 ![]() 次迭代中的记为
次迭代中的记为 ![]() 。
。
(5)就是前面提到的数据项 data term。
(6)就是前面提到的先验项 prior term。
It can be observed that the data term and the prior term are decoupled into Eq. (5) and Eq. (6), respectively.
For the solution of Eq. (5), the fast Fourier transform (FFT) can be utilized by assuming the convolution is carried out with circular boundary conditions. Notably, it has a closed-form expression [71]
where
is defined as
with
and where the
and
denote FFT and inverse FFT,
denotes complex conjugate of
,
denotes the distinct block processing operator with element-wise multiplication, i.e., applying elementwise multiplication to the
distinct blocks of
,
denotes the distinct block downsampler, i.e., averaging the
distinct blocks,
denotes the standard s-fold upsampler, i.e., upsampling the spatial size by filling the new entries with zeros.
It is especially noteworthy that Eq. (7) also works for the special case of deblurring when
.
For the solution of Eq. (6), it is known that, from a Bayesian perspective, it actually corresponds to a denoising problem with noise level
[10].
给出了公式(5)和(6)的解。(公式(6)的解我没看懂,或许要参考一下文献 [10]。)
公式(5)的求解采用了快速傅里叶变换,求解过程可能需要参考一下文献 [71]。
值得注意的是,当 ![]() 时,公式(7)也可以适用于去模糊算法(deblurring )。
时,公式(7)也可以适用于去模糊算法(deblurring )。
Deep unfolding network
Once the unfolding optimization is determined, the next step is to design the unfolding super-resolution network (USRNet). Because the unfolding optimization mainly consists of iteratively solving a data subproblem (i.e., Eq. (5)) and a prior subproblem (i.e., Eq. (6)), USRNet should alternate between a data module D and a prior module P. In addition, as the solutions of the subproblems also take the hyper-parameters αk and βk as input, respectively, a hyper-parameter module H is further introduced into USRNet. Fig. 3 illustrates the overall architecture of USRNet with K iterations, where K is empirically set to 8 for the speed-accuracy trade-off. Next, more details on D, P and H are provided.
一旦展开优化确定,下一步是设计展开超分辨率网络(USRNet)。因为展开优化主要包括迭代求解一个数据子问题 (即式(5)) 和一个先验子问题 (即公式(6)),USRNet 应该轮流一个数据模块 D 和前一个模块 P。此外,子问题的解决方案也把 hyper-parameters ![]()
![]() 作为输入,分别进一步引入 USRNet hyper-parameter 模块 H。图 3 展示了带有
作为输入,分别进一步引入 USRNet hyper-parameter 模块 H。图 3 展示了带有 ![]() 个迭代的 USRNet 的总体架构,其中
个迭代的 USRNet 的总体架构,其中 ![]() 被经验地设置为 8,以权衡速度-准确性。接下来,提供D、P和H的更多细节。
被经验地设置为 8,以权衡速度-准确性。接下来,提供D、P和H的更多细节。
- Data module D
The data module plays the role of Eq. (7) which is the closed-form solution of the data subproblem. Intuitively, it aims to find a clearer HR image which minimizes a weighted combination of the data term
and the quadratic regularization term
with trade-off hyper-parameter
.
Because the data term corresponds to the degradation model, the data module thus not only has the advantage of taking the scale factor
and blur kernel
as input but also imposes a degradation constraint on the solution. Actually, it is difficult to manually design such a simple but useful multiple-input module. For brevity, Eq. (7) is rewritten as
. (8)
Note that
is initialized by interpolating
with scale factor
via the simplest nearest neighbor interpolation. It should be noted that Eq. (8) contains no trainable parameters, which in turn results in better generalizability due to the complete decoupling between data term and prior term. For the implementation, we use PyTorch where the main FFT and inverse FFT operators can be implemented by torch.rfft and torch.irfft, respectively.
数据模块Eq.(7) 的目的是找到一个更清晰的 HR 图像,使最小化加权组合的数据项和二次正则项。
由于数据项对应于退化模型,因此数据模块不仅具有将比例因子和 blur 内核作为输入的优点,而且对解决方案施加了退化约束。实际上,手工设计这样一个简单但有用的多输入模块是很困难的。
为简洁起见,将式(7)改写为公式(8)。数据模块不包含可训练参数(即数据模块没有用深度学习),由于数据项与先验项完全解耦,因此具有更好的泛化能力。
具体实现,傅里叶变换与反变换可用 torch.rfft and torch.irfft 函数实现。
Figure 3. The overall architecture of the proposed USRNet with
iterations. USRNet can flexibly handle the classical degradation (i.e., Eq. (1)) via a single model as it takes the LR image
, scale factor
, blur kernel
and noise level
as input. Specifically, USRNet consists of three main modules, including the data module D that makes HR estimation clearer, the prior module P that makes HR estimation cleaner, and the hyper-parameter module H that controls the outputs of D and P.
- Prior module P
The prior module aims to obtain a cleaner HR image
by passing
through a denoiser with noise level
. Inspired by [66], we propose a deep CNN denoiser that takes the noise level as input
. (9)
The proposed denoiser, namely ResUNet, integrates residual blocks [21] into U-Net [45]. U-Net is widely used for image-to-image mapping, while ResNet owes its popularity to fast training and its large capacity with many residual blocks. ResUNet takes the concatenated
and noise level map as input and outputs the denoised image
. By doing so, ResUNet can handle various noise levels via a single model, which significantly reduces the total number of parameters. Following the common setting of U-Net, ResUNet involves four scales, each of which has an identity skip connection between downscaling and upscaling operations. Specifically, the number of channels in each layer from the first scale to the fourth scale are set to 64, 128, 256 and 512, respectively. For the downscaling and upscaling operations,
strided convolution (SConv) and
transposed convolution (TConv) are adopted, respectively. Note that no activation function is followed by SConv and TConv layers, as well as the first and the last convolutional layers. For the sake of inheriting the merits of ResNet, a group of 2 residual blocks are adopted in the downscaling and upscaling of each scale. As suggested in [36], each residual block is composed of two
convolution layers with ReLU activation in the middle and an identity skip connection summed to its output.
先验模块的目的是通过带噪声级的降噪器传递 ![]() 来获得更清晰的 HR 图像。受到 [66] 的启发,提出了一种深度CNN降噪器,以噪声水平作为输入。
来获得更清晰的 HR 图像。受到 [66] 的启发,提出了一种深度CNN降噪器,以噪声水平作为输入。
先验模块由 ResUNet 构成。具体细节包括:
1) U-Net 包括 4 层;
2) 每层的下采样用 ![]() 步进卷积 SConv;没有跟激活函数;
步进卷积 SConv;没有跟激活函数;
3) 每层的上采样用 ![]() 反卷积 TConv;没有跟激活函数;
反卷积 TConv;没有跟激活函数;
4) 每个编解码器包括两个 residual block;卷积是 ![]() 的;结构如文献 【2017CVPRW Enhanced deep residual networks for single 9 image super-resolution】,下图这个样子的。
的;结构如文献 【2017CVPRW Enhanced deep residual networks for single 9 image super-resolution】,下图这个样子的。
- Hyper-parameter module H
The hyper-parameter module acts as a ‘slide bar’ to control the outputs of the data module and prior module. For example, the solution
would gradually approach
as
increases. According to the definition of
and
,
is determined by
and
, while
depends on
and
. Although it is possible to learn a fixed
and
, we argue that a performance gain can be obtained if
and
vary with two key elements, i.e., scale factor
and noise level
, that influence the degree of ill-posedness. Let
and
, we use a single module to predict
and
. (10)
The hyper-parameter module consists of three fully connected layers with ReLU as the first two activation functions and Softplus [19] as the last. The number of hidden nodes in each layer is 64. Considering the fact that
and
should be positive, and Eq. (7) should avoid division by extremely small
, the output Softplus layer is followed by an extra addition of 1e-6. We will show how the scale factor and noise level affect the hyper-parameters in Sec. 4.4.
超参数模块由三个完全连接的层组成,ReLU 作为前两个激活函数,Softplus[19] 作为后两个激活函数。每一层的隐藏节点数为 64个。考虑到 ![]() 和
和 ![]() 应该为正,且 Eq.(7) 应该避免被极小除法,输出 Softplus 层后面是额外添加的 1e-6。在第 4.4 节中展示尺度因子和噪声水平如何影响超参数。
应该为正,且 Eq.(7) 应该避免被极小除法,输出 Softplus 层后面是额外添加的 1e-6。在第 4.4 节中展示尺度因子和噪声水平如何影响超参数。
三个模块中,D 用的是基于模型的方法(非深度学习);P 和 H 是深度学习模型;这就是 Introduction 中说的,本文的方法是结合了二者的方法。
End-to-end training
The end-to-end training aims to learn the trainable parameters of USRNet by minimizing a loss function over a large training data set. Thus, this section mainly describe the training data, loss function and training settings. Following [58], we use DIV2K [3] and Flickr2K [55] as the HR training dataset. The LR images are synthesized via Eq. (1). Although USRNet focuses on SISR, it is also applicable to the case of deblurring with
. Hence, the scale factors are chosen from {1, 2, 3, 4}. However, due to limited space, this paper does not consider the deblurring experiments. For the blur kernels, we use anisotropic Gaussian kernels as in [44, 51, 67] and motion kernels as in [5]. We fix the kernel size to 25×25. For the noise level, we set its range to [0, 25].
With regard to the loss function, we adopt the L1 loss for PSNR performance. Following [58], once the model is obtained, we further adopt a weighted combination of L1 loss, VGG perceptual loss and relativistic adversarial loss [24] with weights 1, 1 and 0.005 for perceptual quality performance. We refer to such fine-tuned model as USRGAN. As usual, USRGAN only considers scale factor 4. We do not use additional losses to constrain the intermediate outputs since the above losses work well. One possible reason is that the prior module shares parameters across iterations.
To optimize the parameters of USRNet, we adopt the Adam solver [27] with mini-batch size 128. The learning rate starts from
and decays by a factor of 0.5 every
iterations and finally ends with
. It is worth pointing out that due to the infeasibility of parallel computing for different scale factors, each min-batch only involves one random scale factor. For USRGAN, its learning rate is fixed to
. The patch size of the HR image for both USRNet and USRGAN is set to
. We train the models with PyTorch on 4 Nvidia Tesla V100 GPUs in Amazon AWS cloud. It takes about two days to obtain the USRNet model.
讲了一下网络参数的设置。
USRNet:只采用 L1 Loss。
USRGAN:采用 L1 Loss、VGG Loss、relativistic adversarial Loss。
二者的学习率设置也不同。
Experiments
We choose the widely-used color BSD68 dataset [40, 46] to quantitatively evaluate different methods. The dataset consists of 68 images with tiny structures and fine textures and thus is challenging to improve the quantitative metrics, such as PSNR. For the sake of synthesizing the corresponding testing LR images via Eq. (1), blur kernels and noise levels should be provided. Generally, it would be helpful to employ a large variety of blur kernels and noise levels for a thorough evaluation, however, it would also give rise to burdensome evaluation process. For this reason, as shown in Table 1, we only consider 12 representative and diverse blur kernels, including 4 isotropic Gaussian kernels with different widths (i.e., 0.7, 1.2, 1.6 and 2.0), 4 anisotropic Gaussian kernels from [67], and 4 motion blur kernels from [5, 33]. While it has been pointed out that anisotropic Gaussian kernels are enough for SISR task [44, 51], the SISR method that can handle more complex blur kernels would be a preferred choice in real applications. Therefore, it is necessary to further analyze the kernel robustness of different methods, we will thus separately report the PSNR results for each blur kernel rather than for each type of blur kernels. Although it has been pointed out that the proper blur kernel should vary with scale factor [64], we argue that the 12 blur kernels are diverse enough to cover a large kernel space. For the noise levels, we choose 2.55 (1%) and 7.65 (3%).
评价实验中的一些设置,如数据集的选择,核的选择,噪声等级的选择。
PSNR results
The compared methods include RCAN [70], ZSSR [51], IKC [20] and IRCNN [65]. Specifically, RCAN is stateof-the-art PSNR oriented method for bicubic degradation; ZSSR is a non-blind zero-shot learning method with the ability to handle Eq. (1) for anisotropic Gaussian kernels; IKC is a blind iterative kernel correction method for isotropic Gaussian kernels; IRCNN a non-blind deep denoiser based plug-and-play method.
Table 1. Average PSNR(dB) results of different methods for different combinations of scale factors, blur kernels and noise levels. The best two results are highlighted in red and blue colors, respectively.
对几个典型的 SISR 算法进行介绍和 PSNR 比较。
Although USRNet is not designed for bicubic degradation, it is interesting to test its results by taking the approximated bicubic kernels in Fig. 2 as input. From Table 2, one can see that USRNet still performs favorably without training on the bicubic kernels.
Table 2. The average PSNR(dB) results of USRNet for bicubic degradation on commonly-used testing datasets.
虽然 USRNet 不是为双三次退化设计的,但是以 图2 中近似的双三次核作为输入来测试其结果是很有趣的。从 表2 可以看出,USRNet 在没有经过双三次内核训练的情况下仍然表现良好。
Visual results
Figure 4. Visual results of different methods on super-resolving noise-free LR image with scale factor 4. The blur kernel is shown on the upper-right corner of the LR image. Note that RankSRGAN and our USRGAN aim for perceptual quality rather than PSNR value.
Analysis on D and P
Because the proposed USRNet is an iterative method, it is interesting to investigate the HR estimations of data module D and prior module P in different iterations. Fig. 5 shows the results of USRNet and USRGAN in different iterations for an LR image with scale factor 4. As one can see, D and P can facilitate each other for iterative and alternating blur removal and detail recovery. Interestingly, P can also act as a detail enhancer for high-frequency recovery due to the task-specific training. In addition, it does not reduce blur kernel induced degradation which verifies the decoupling between D and P. As a result, the end-to-end trained USRNet has a task-specific advantage over Gaussian denoiser based plug-and-play SISR. To quantitatively analyze the role of D, we have trained an USRNet model with 5 iterations, it turns out that the average PSNR value will decreases about 0.1dB on Gaussian blur kernels and 0.3dB on motion blur kernels. This further indicates that D aims to eliminate blur kernel induced degradation. In addition, one can see that USRGAN has similar results with USRNet in the first few iterations, but will instead recover tiny structures and fine textures in last few iterations.
Figure 5. HR estimations in different iterations of USRNet (top row) and USRGAN (bottom row). The initial HR estimation
is the nearest neighbor interpolated version of LR image. The scale factor is 4, the noise level of LR image is 2.55 (1%), the blur kernel is shown on the upper-right corner of
.
由于所提出的USRNet是一种迭代方法,因此研究数据模块 D 和先验模块 P 在不同迭代下的 HR 估计是很有意义的。
图5 为比例因子为 4 的 LR 图像的 USRNet 和 USRGAN 在不同迭代下的结果。
D 和 P 可以互相促进迭代和交替模糊去除和细节恢复。有趣的是,由于特定任务的训练,P 也可以作为高频恢复的细节增强剂。此外,它并没有减少模糊核引起的退化,这验证了 D 和 P 之间的解耦,因此,端到端训练的 USRNet 比基于高斯去噪即插即用的SISR 具有任务特定的优势。
为了定量分析 D 的作用,训练了一个 5 次迭代的 USRNet 模型,结果表明,在高斯模糊内核上,平均 PSNR 值会降低约 0.1dB,在运动模糊内核上,平均 PSNR 值会降低约 0.3dB。
这进一步表明 D 的目标是消除模糊核引起的退化。此外,可以看到 USRGAN 在前几个迭代中与 USRNet 有类似的结果,但是在最后几个迭代中将恢复微小的结构和精细的纹理。
Analysis on H
Fig. 6 shows outputs of the hyper-parameter module for different combinations of scale factor
and noise level
. It can be observed from Fig. 6(a) that
is positively correlated with
and varies with s. This actually accords with the definition of
in Sec. 3.2 and our analysis in Sec. 3.3. From Fig. 6(b), one can see that
has a decreasing tendency with the number of iterations and increases with scale factor and noise level. This implies that the noise level of HR estimation is gradually reduced across iterations and complex degradation requires a large
to tackle with the illposeness. It should be pointed out that the learned hyperparameter setting is in accordance with that of IRCNN [65]. In summary, the learned H is meaningful as it plays the proper role.
Figure 6. Outputs of the hyper-parameter module H, i.e., (a)
and (b)
, with respect to different combinations of
and
.
图6显示了不同组合 hyper-parameter 模块的输出比例因子和噪声 ![]() 水平。它可以观察到从图 6 (a),
水平。它可以观察到从图 6 (a),![]() 与
与 ![]() 呈正相关,而与
呈正相关,而与 ![]() 相反。这实际上符合
相反。这实际上符合 ![]() 的定义在3.2节。
的定义在3.2节。
从图 6 (b),一个可以看到 ![]() 随比例因子和噪声水平的增加,有减少的趋势。
随比例因子和噪声水平的增加,有减少的趋势。
综上所述,所学的 H 是有意义的,因为它发挥了适当的作用。
Generalizability
As mentioned earlier, the proposed method enjoys good generalizability due to the decoupling of data term and prior term. To demonstrate such an advantage, Fig. 7 shows the visual results of USRNet and USRGAN on LR image with a kernel of much larger size than training size of 25×25. It can be seen that both USRNet and USRGAN can produce visually pleasant results, which can be attributed to the trainable parameter-free data module. It is worth pointing out that USRGAN is trained on scale factor 4, while Fig. 7(b) shows its visual result on scale factor 3. This further indicates that the prior module of USRGAN can generalize to other scale factors. In summary, the proposed deep unfolding architecture has superiority in generalizability.
Figure 7. An illustration to show the generalizability of USRNet and USRGAN. The sizes of the kernels in (a) and (c) are 67×67 and 70×70, respectively. The two kernels are chosen from [41].
如前所述,由于数据项和先验项的解耦,该方法具有很好的推广性。为了说明这种优势,图7显示了 USRNet 和 USRGAN 在 LR 图像上的视觉结果,其核尺寸比训练尺寸 ![]() 大得多。可以看出,USRNet和USRGAN都可以产生视觉上令人愉悦的结果,这要归功于可训练的无参数数据模块。值得指出的是,USRGAN 在scale factor 4上进行了训练,而 图7(b) 显示了其在 scale factor 3 上的可视化结果。这进一步表明 USRGAN 的先验模块可以推广到其他尺度因子。综上所述,所提出的深度展开结构具有普遍的优越性。
大得多。可以看出,USRNet和USRGAN都可以产生视觉上令人愉悦的结果,这要归功于可训练的无参数数据模块。值得指出的是,USRGAN 在scale factor 4上进行了训练,而 图7(b) 显示了其在 scale factor 3 上的可视化结果。这进一步表明 USRGAN 的先验模块可以推广到其他尺度因子。综上所述,所提出的深度展开结构具有普遍的优越性。
Real image super-resolution
Because Eq. (7) is based on the assumption of circular boundary condition, a proper boundary handling for the real LR image is generally required. We use the following three steps to do such pre-processing. First, the LR image is interpolated to the desired size. Second, the boundary handling method proposed in [38] is adopted on the interpolated image with the blur kernel. Last, the downsampled boundaries are padded to the original LR image. Fig. 8 shows the visual result of USRNet on real LR image with scale factor 4. The blur kernel is manually selected as isotropic Gaussian kernel with width 2.2 based on user preference. One can see from Fig. 8 that the proposed USRNet can reconstruct the HR image with improved visual quality.
Figure 8. Visual result of USRNet (×4) on a real LR image.
由于式 (7) 是基于圆形边界条件的假设,因此通常需要对真实 LR 图像进行适当的边界处理。我们使用以下三个步骤来进行这种预处理。首先,将 LR 图像内插到所需的大小。其次,对带模糊核的插值图像采用了 [38] 中提出的边界处理方法。最后,将下采样边界填充到原始 LR 图像。图8 显示了 USRNet 在实际 LR 图像上的可视结果,比例因子为 4。基于用户喜好,手动选择模糊核作为宽度为 2.2 的各向同性高斯核。从 图8 可以看出,提出的 USRNet 可以重建出视觉质量得到改善的 HR 图像。
之所以加这一小结,是因为本文的摘要、前言提及过对真实图像有效,本节就是对这几句话做出的验证。
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第1张图片](http://img.e-com-net.com/image/info8/9b2143b0222944199e805c0e3d59a792.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第2张图片](http://img.e-com-net.com/image/info8/664945b4d031487a8c87ebf3cacf5ad5.jpg)

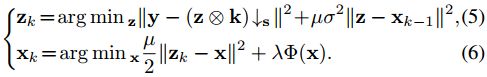
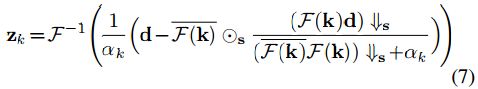
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第3张图片](http://img.e-com-net.com/image/info8/808d1123880047baba57f80bd6cd7b75.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第4张图片](http://img.e-com-net.com/image/info8/7ee5e327d61b4cd2a2e5be61153e3236.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第5张图片](http://img.e-com-net.com/image/info8/67ee9261d41d45fda680dae95b49f029.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第6张图片](http://img.e-com-net.com/image/info8/29fb8ac5ab374204a62a46456166b423.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第7张图片](http://img.e-com-net.com/image/info8/36bfffbeada64f9c983ad6370e24dc03.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第8张图片](http://img.e-com-net.com/image/info8/b8cba26c778a49aba5129cd253078021.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第9张图片](http://img.e-com-net.com/image/info8/555da075faf64dc3820ce4c9fb811df6.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第10张图片](http://img.e-com-net.com/image/info8/0df5797982e74eb5bd11e2bf00a6a88d.jpg)
![MyDLNote-Enhancment: [SR转文] Deep Unfolding Network for Image Super-Resolution_第11张图片](http://img.e-com-net.com/image/info8/f27442897e9948858d1dffb5bdfbc9e9.jpg)