深度学习系列（1）——从线性回归说起

为什么先说线性回归

本文适合入门级同学，老司机绕行。
吴恩达老师的机器学习课程，介绍的第一个模型就是线性回归模型。机器学习（尤其是监督学习），主要围绕分类和回归两类问题展开，而线性回归模型作为最简单的回归模型，与大多数监督学习算法具有相同的建模思路，包括建立损失函数、优化参数、模型评估。可谓麻雀虽小五脏俱全，了解线性回归的建模思想能够有助于理解复杂的深度学习模型。

---

什么是线性回归：一个简单的例子

import numpy as np
from numpy import random
import matplotlib.pyplot as plt

X = random.uniform(0, 30, 100) # 随机生成在[0,30]区间内服从均匀分布的100个数
y = 1.85 * X + random.normal(2, 5, 100) # 对X乘以固定系数后加上随机扰动

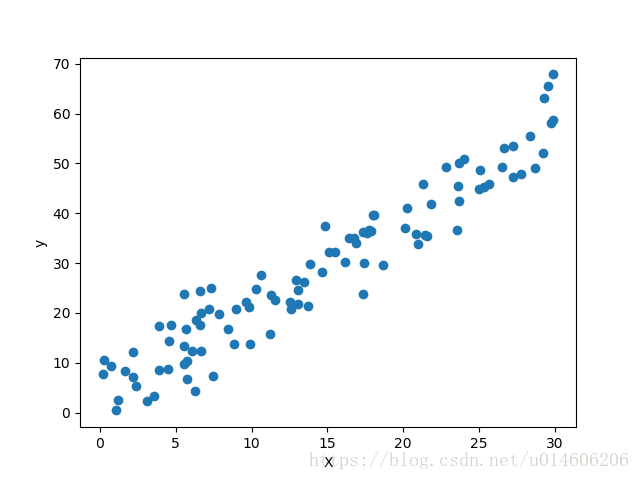
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.show()

以上代码随机生成一组样本X和y，现在给定一组X值，需要预测其对应的y值。

解决这个问题的思路如下：

• 假设X和y之间存在线性关系，即 y=w∗X+b y = w ∗ X + b ;
• y^=wX+b y ^ = w X + b ，其中 y^ y ^ 表示根据线性方程计算得到的 y y 值（称为估计值），为尽可能准确的表达样本中X和y之间的关系，我们需要找到最优的 w∗ w ∗ 和 b∗ b ∗ ，使得 y y 的实际值和估计值之间的误差 |y−y^| | y − y ^ | 最小化。

以上问题中 X X 称为自变量， y y 称为因变量，找到最优直线方程 y=w∗X+b∗ y = w ∗ X + b ∗ ，使得因变量的估计值与实际值之间的误差最小的过程，称为线性回归。

---

线性回归模型的数学推导

• 将所有样本点用坐标表示为 (xi,yi) ( x i , y i ) ， i={1,2,...,m} i = { 1 , 2 , . . . , m } ，即共有m各样本点.
• 假设线性方程形式为 y=wX+b y = w X + b ，则对于所有的 i i ： yi^=wxi+b y i ^ = w x i + b .
• 样本误差可表示为：
  
  loss=∑i=1m|yi^−yi| l o s s = ∑ i = 1 m | y i ^ − y i |
  ⇓ ⇓
  loss=∑i=1m|wxi+b−yi| l o s s = ∑ i = 1 m | w x i + b − y i |
• 找到最优参数 w∗ w ∗ 和 b∗ b ∗ 使得样本误差 loss l o s s 值最小，此时可将 loss l o s s 看成是关于 w w 和 b b 的函数，即求解无约束最优化问题：
  minloss=∑i=1m|wxi+b−yi| m i n l o s s = ∑ i = 1 m | w x i + b − y i |
• 虽然线性回归可采用最小二乘法求解，但是相对梯度下降法来说，最小二乘法在机器学习中具有很大的局限性，因此本文介绍梯度下降法求解线性回归问题，计算梯度需要对目标函数求偏导，而上面这种形式的目标函数不便于求偏导，因而转换成误差平方和形式：
  minloss=∑i=1m(wxi+b−yi)2. m i n l o s s = ∑ i = 1 m ( w x i + b − y i ) 2 .
• 梯度下降法主要思想为通过不断迭代使得解沿着目标函数值下降的方向变化，知道达到指定的精度或是迭代到一定的次数才终止，从而逼近最优解。设函数形式为 f(x,y) f ( x , y ) ，则当前最优解为 [xk,yk] [ x k , y k ] ，梯度计算方式为 [∂f∂x,∂f∂y] [ ∂ f ∂ x , ∂ f ∂ y ] ，设更新最优解得步长为 λ λ ，则更新后的最优解为：
  [xk+1,yk+1]=[xk,yk]−λ[∂f∂x,∂f∂y] [ x k + 1 , y k + 1 ] = [ x k , y k ] − λ [ ∂ f ∂ x , ∂ f ∂ y ]
  实际中常用的梯度下降法为随机梯度下降法（SGD）和批梯度下降法(BGD)，关于梯度下降算法比较复杂，本文不展开讨论，以后补充。

---

Keras实现线性回归

- 导入相关模块

# coding: utf8

import numpy as np
from numpy import random
import matplotlib.pyplot as plt

from keras.layers import Input, Dense
from keras.optimizers import SGD
from keras.models import Model
from keras.utils import plot_model

- 随机生成数据集（与本文最开始重复，但为保证连贯性，此处重写）

X = random.uniform(0, 30, 100)  # 随机生成在[0,30]区间内服从均匀分布的100个数
y = 1.85 * X + random.normal(0, 2, 100)  # 对X乘以固定系数后加上随机扰动

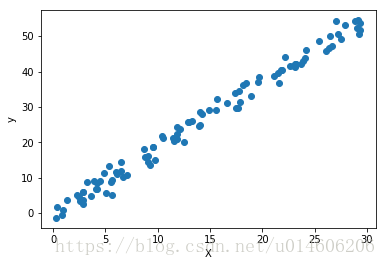
plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
plt.show() # 查看数据散点图

• keras构建线性回归模型

input_shape = (1,)  # 声明输入tensor的shape
input_tensor = Input(shape=input_shape)  # 由于输入必须是tensor，所以通过Input函数根据指定的输入tensor的shape，生成输入tensor
predict = Dense(1, activation='linear', name='output')(input_tensor)  # 通过Dense函数添加回归函数，指定为'linear'即为线性函数，函数输入为输入tensor
model = Model(inputs=input_tensor, outputs=predict)  # 生成model，并指定输入和输出
print(model.summary())  # 查看生成的模型结构

从model.summary()输出的结果可以看到：输入层仅仅是将输入数据转变成tensor，而shape不变，所以输入的shape为(None, 1)，None表示输入的样本数据数量，此处由于没有指定具体的输入，所以对应值为None，shape里面的1表示输入样本的维度；output层的输出shape与输入层一样，表示输出值得维度也为1，与本文线性回归的样本数据维度一致；输出层的参数数为2，表示有2个参数需要训练，对应前文的 w w 和 b b 。

• 训练模型

# 编译模型：loss参数指定损失函数为均方误差，optimizer指定优化算法为随机梯度下降法，学习率为0.01，作为入门，不必过于关心优化算法的参数
model.compile(loss='mse', optimizer=SGD(lr=0.01)) 
# 训练模型：指定样本输入和输出，将训练样本中的20%作为验证集评估模型效果
train_history = model.fit(X, y, validation_split=0.2,
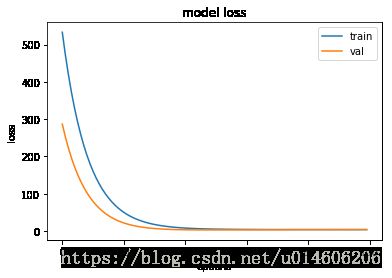
                          epochs=100, batch_size=100, verbose=2)

从上面过程可以看出，在Keras里面搭建模型，就跟搭积木一样，非常方便！

• 查看训练过程中目标函数收敛过程
  

可以看到，在迭代到40次左右，目标函数就收敛到最小值，也就是得到了最有参数 w∗ w ∗ 和 b∗ b ∗ 。

• 查看训练得到的模型参数

[w, b] = model.layers[1].get_weights()
print(w, b)

[[1.8470368]] [0.06696377]

输出结果显示 w∗=1.847,b∗=0.0669 w ∗ = 1.847 , b ∗ = 0.0669 ，而我们生成数据的函数为 y=1.85x y = 1.85 x 加上均值为0标准差为2的随机扰动项，即 w∗=1.85,b∗=0 w ∗ = 1.85 , b ∗ = 0 ，因此可以认为得到的最优权重非常接近真实值。

通过model.layer可以得到模型中所有的层，并通过索引指定特定层，通过get_weights()函数获取对应层的参数。

• 画出拟合直线

plt.scatter(X, y)
plt.xlabel('X')
plt.ylabel('y')
x1 = np.linspace(0, 30, 1000)
y1 = w[0][0]*x1 + b[0]
plt.plot(x1, y1, 'r')

从图可以看出，回归直线与样本数据的变化趋势吻合的非常好！

---

本文结束。