【剑指offer题解 整理版】树
- 树
- 考察点
- 树的下一个结点
- 对称二叉树
- 镜像二叉树
- 把二叉树打印成多行
- 按之字形顺序打印二叉树
- 从上往下打印二叉树
- 序列化与反序列化二叉树
- 二叉树中和为某一值的路径
- 二叉树的深度
- 二叉搜索树的第k个结点
- 二叉搜索树与双向链表
树
考察点
树的数据结构特性
- 树的遍历规律、遍历序列特点: 树的下一个结点
- 树与递归: 对称二叉树、镜像二叉树
- 树与层序遍历:把二叉树打印成多行、按之字打印二叉树、序列化和反序列化二叉树、从上往下打印二叉树
- 二叉树与路径: 二叉树中和为某一值的路径
- 二叉树与深度: 二叉树的深度
- 二叉搜索树:二叉搜索树的第k个结点、二叉搜索树与双向链表
树的下一个结点
从树的中序遍历的规则分析一下,树的下一结点分几种情况?跟什么有关?
树的中序遍历序列的每一个part都遵循左根右(忽略空子树)的顺序规则。
由此可得出一个大致的结论,next结点要么与右子树有关,要么与根结点有关。
下面我们借助几个实例具体分析一下求树的下一个结点的问题,我们设想几种情况,先考虑最简化的情况,一个二层的二叉树:
- pNode为根节点,那么当它右子树不为空时,下一结点为右子树为右子树的最左叶结点,当右子树为空时,next结点为空。
- pNode为根的左结点时,next结点为父结点
- pNode为根的右结点时,next结点为空。
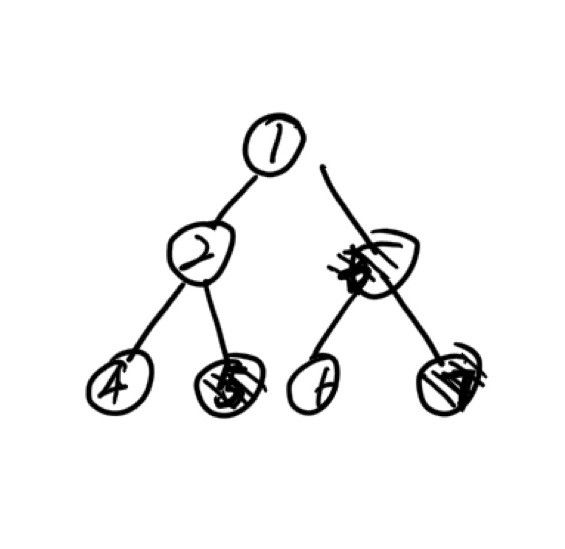
进一步,考虑较为复杂的情况,一个三层的二叉树:
- pNode为根节点,那么当它右子树不为空时,下一结点为右子树为右子树的最左叶结点,当右子树为空时,next结点为空。
- pNode是父结点的左孩子时,next结点为父结点。
- pNode是父结点的右孩子时,next结点为:
- 如pNode有右子树,那么next结点为右子树的最左叶节点
- 如pNode没有右子树,那么next结点分两种情况:
- 父节点的父结点为空,next结点为空(如图中结点3的情况)。
- 父节点是它父节点的左孩子,next结点为祖父结点(如图中结点5的情况)
- pNode的父亲结点是其父节点的右孩子,那么next结点为空(如途中结点7的情况)。
对于三层的二叉树的分析已经接近一般性的二叉树了,我们再自己分析一下就可以推断出,对于更多层数的二叉树也是这样的。
此外,我们可以继续简化上述的规律,我们发现处理情况1和情况3的规则几乎是一样的,因此可以合并一下:
next结点只与右子树、父结点、祖父结点有关,规律如下:
1. pNode为根节点或者pNode是其父结点的右孩子时,next结点为:
- **如果pNode有右子树**,那么next结点为右字树的最左叶节点
- **如果pNode没有右子树**,那么next结点分为3种情况:
- **pNode的父结点为空或祖父结点为空**,next结点为空
- **pNode的父节点是祖父结点的左孩子**,next结点为祖父结点
- **pNode的父亲结点是祖父结点的右孩子**,那么next结点为空。
pNode为根的左结点时:
- 右子树为空,next结点为父结点
- 右子树非空,next结点为右子树的最左边结点
接下来我们就可以开始写程序了。
/*
struct TreeLinkNode {
int val;
struct TreeLinkNode *left;
struct TreeLinkNode *right;
struct TreeLinkNode *next;
TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {
}
};
*/
class Solution {
public:
TreeLinkNode* GetNext(TreeLinkNode* pNode)
{
// 边界情况
if(pNode == NULL) return NULL;
if(pNode->next==NULL || pNode==pNode->next->right)
{
// pNode右子树为空
if(pNode->right == NULL)
{
return GetNextHelper(pNode);
}
// pNode有右子树
else
{
// 右子树的最左叶节点
return GetLeftestLeaf(pNode->right);
}
}
if(pNode == pNode->next->left)
{
// 右子树为空
if(pNode->right == NULL)
return pNode->next;
//右子树非空
else
return GetLeftestLeaf(pNode->right);
}
//为了编译通过
return NULL;
}
TreeLinkNode* GetNextHelper(TreeLinkNode *pRoot)
{
// pNode父节点为空
if(pRoot->next == NULL || pRoot->next->next==NULL) return NULL;
// pNode父节点为组父节点的左孩子
if(pRoot->next == pRoot->next->next->left)
return pRoot->next->next;
// pNode父节点为祖父节点的右孩子
if(pRoot->next == pRoot->next->next->right)
{
return NULL;
}
//为了编译通过
return NULL;
}
TreeLinkNode* GetLeftestLeaf(TreeLinkNode* pRoot)
{
TreeLinkNode *left = pRoot->left;
if(left==NULL)
return pRoot;
else
return GetLeftestLeaf(left);
}
};测试:
int main()
{
TreeLinkNode* p8 = new TreeLinkNode(8);
TreeLinkNode* p6 = new TreeLinkNode(6);
TreeLinkNode* p10 = new TreeLinkNode(10);
TreeLinkNode* p5 = new TreeLinkNode(5);
TreeLinkNode* p7 = new TreeLinkNode(7);
TreeLinkNode* p9 = new TreeLinkNode(9);
TreeLinkNode* p11 = new TreeLinkNode(11);
p8->left = p6;
p8->right = p10;
p6->left = p5;
p6->right = p7;
p6->next = p8;
p10->left = p9;
p10->right = p11;
p10->next = p8;
p5->next = p6;
p7->next = p6;
p9->next = p10;
p11->next = p10;
Solution s;
TreeLinkNode* next = s.GetNext(p6);
// cout<
if(next)
{
std::cout<<next->val<<std::endl;
}
return 0;
} 另一种思路:
上面我们从父节点与祖父结点的关系分类分析,还可以从有无右子树进行分析,ac代码如下,可以对比分析一下:
/*
struct TreeLinkNode {
int val;
struct TreeLinkNode *left;
struct TreeLinkNode *right;
struct TreeLinkNode *next;
TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {
}
};
*/
class Solution {
public:
TreeLinkNode* GetNext(TreeLinkNode* pNode)
{
if(pNode == NULL) return NULL;
if(pNode->right == NULL)
//
{
return GetF(pNode);
}
else
//
return GetLeftestLeaf(pNode->right);
}
TreeLinkNode* GetF(TreeLinkNode *pRoot)
{
if(pRoot->next == NULL) return NULL;
if(pRoot == pRoot->next->left)
return pRoot->next;
if(pRoot == pRoot->next->right)
{
if(pRoot->next->next == NULL || pRoot->next == pRoot->next->next->right)
return NULL;
else
return pRoot->next->next;
}
return NULL;
}
TreeLinkNode* GetLeftestLeaf(TreeLinkNode* pRoot)
{
TreeLinkNode *left = pRoot->left;
if(left==NULL)
return pRoot;
else
return GetLeftestLeaf(left);
}
};对称二叉树
如何判断一颗二叉树是否是对称二叉树?对称二叉树符合什么规则,如何对二叉树进行递归遍历以便判定对称二叉树?
我们先大概设想一下:
一棵树是对称二叉树的话,树中除了根结点外的每个对称位置的结点同时为空或者值相同。
由此可得出一个大概的结论,树的对称位置相同的树是对称二叉树。
下面借助几个具体的实例分析一下判定对称二叉树的问题,我们设想几种情况,先考虑最简化的情况,一个空树和只有一个根结点的树:
它一定是对称二叉树。
- 左右结点都空时(就是一层的二叉树),对称
- 左空右不空或左不空右空,不对称
- 左右都不空但值不相等,不对称
- 左右都不空且值相等,对称
1234规则简而言之:
一棵两层的二叉树是否对称,取决于左?=右
一颗三层的二叉树是否对称,取决于
左?=右
左左?=右右
左右?=右左 对于三层的二叉树的分析已经接近一般性的二叉树了,我们再自己分析一下就可以推断出,对于更多层数的二叉树也有类似的规则,比如一如下的4层二叉树:
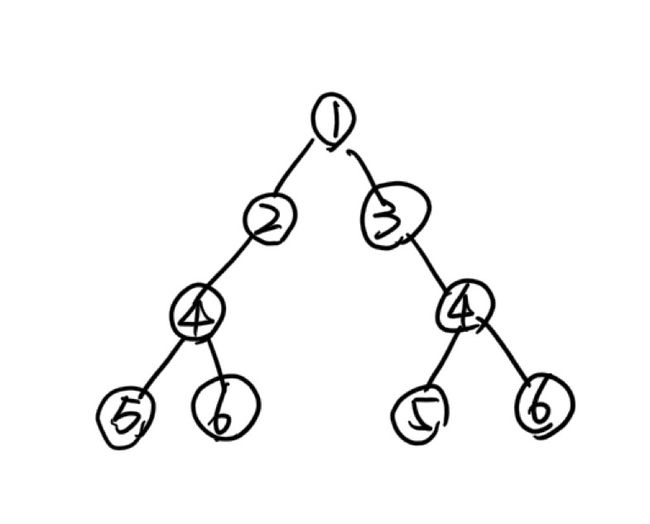
前三层的判定如上所述,第四层是否对称取决于左左左?=右右右,左左右?=右右左
我们归纳出对称二叉树的一般规则;
1. 从根节点出发,判断其左孩子”?=”右孩子,如果相等,前两层是对称的
2. 如果前两层对称,那么我们继续比较下一层,当前结点为根的左孩子和根的右孩子,比较:
-根的左孩子的左孩子”?=”根的右孩子的右孩子
-根的左孩子的右孩子”?=”根的右孩子的左孩子
如果都相等,那么说明该层对称,递归判断下一层(将[左左,右右]作为新的结点重新执行第2布,同理将[左右,右左]作为当前参数进入第2步,两个结果相与就是该层判断对称的结果),如果两个中有一个不等,一定不对称,结束递归返回结果。
简化一下上面的规则:
我们看到1、2的逻辑中,第2层的逻辑和第3层及以后一样,可以合并为:
从根结点出发,当前开始状态为判断根的左孩子和右孩子,比较:
- 左左?=右右
- 左右?=右左
如果都相等,那么说明该层对称,递归判断下一层(将[左左,右右]作为新的结点重新执行第2布,同理将[左右,右左]作为当前参数进入第2步,两个结果相与就是该层判断对称的结果),如果两个中有一个不等,一定不对称,结束递归返回结果。
接下来我们就可以开始写程序了。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
bool isSymmetrical(TreeNode* pRoot)
{
if(pRoot == NULL) return true;
//if(pRoot->left==NULL && pRoot->right==NULL) return true;
//if(pRoot->left==NULL && pRoot->right!=NULL) return false;
//if(pRoot->right==NULL && pRoot->left!=NULL) return false;
//if(pRoot->left->val != pRoot->right->val) return false;
return helper(pRoot->left, pRoot->right);
}
bool helper(TreeNode *left, TreeNode* right)
{
if(left==NULL && right==NULL) return true;
if(left==NULL && right!=NULL) return false;
if(right==NULL && left != NULL) return false;
if(left->val != right->val) return false;
return helper(left->left, right->right)&& helper(left->right,right->left);
}
};镜像二叉树
如何将一颗二叉树镜像化?采用什么遍历顺序?才遍历过程中如何操作。
我们先大致分析一下:
镜像二叉树,实际上是一个将原二叉树每一个结点的左右孩子的值交换形成的二叉树。进行交换操作的结点顺序可以变,只要保证每个结点都要交换且交换一次即可。
最直观的交换顺序就是前序遍历(其实也可以使用后续遍历),在遍历过程中交换左右孩子的指向即可。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
void Mirror(TreeNode *pRoot) {
if(pRoot == NULL) return;
TreeNode *tmp = pRoot->left;
pRoot->left = pRoot->right;
pRoot->right = tmp;
Mirror(pRoot->left);
Mirror(pRoot->right);
}
};为什么不可以中序遍历?
想象一个三层二叉树,如果使用中序遍历并在遍历时交换结点的左右孩子的值,那么根节点的左子树镜像后,根节点交换左右孩子,左子树变为新的右子树,接下来镜像化右子树其实是将左自述又镜像化了一遍。也就是说左右子树交换了位置,左子树被镜像了2次,右子树被镜像化0次。不符合我们的设想。因此中序遍历不行,可以使用前序或者后序遍历。
也可以非递归遍历这个二叉树,并交换每个结点的左右孩子,AC代码如下,可以对比分析一下:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
stack st;
void Mirror(TreeNode *pRoot) {
if(pRoot == NULL)
return;
st.push(pRoot);
while(st.size()>0)
{
TreeNode* top = st.top();
st.pop();
if(top->left)
st.push(top->left);
if(top->right)
st.push(top->right);
TreeNode* temp = top->left;
top->left = top->right;
top->right = temp;
}
}
}; 把二叉树打印成多行
把二叉树打印成多行,换句话说就是要层序遍历二叉树,我们可以借助二叉树的什么特点以及借助什么数据结构层序遍历二叉树呢?
我们先大致分析一下:
“二”叉树,具备本层的每一个结点都对应下一层的两个结点(左孩子和右孩子,孩子可能为空),也就是说,已知本层的结点,就可找到下一层的结点。
下面我们借助实例具体分析一下:
因为问题比较简单,我们直接分析一个具有一般化特点的三层树形结构:
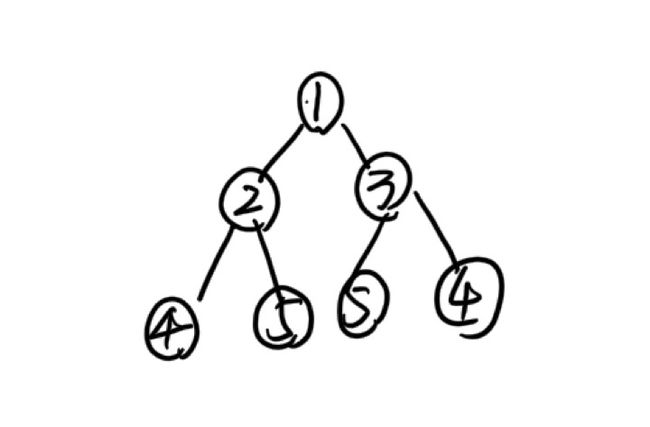
1. 打印第1层,也就是根节点的值
2. 从左到右打印第2层,也就是根的左孩子和右孩子的值
3. 从左到右打印第3层,我们需要找到第2层的结点,分别打印其每个结点的左孩子和右孩子的值。
我们发现,123步骤有一个共有的逻辑,就是打印一层是需要已知上一层结点,然后从上到下一层一层打印,因此,我们借助一个data来保存上一层的结点,比如对于第1层,data为空,对于第2层,data为根结点…,那么data采用什么数据结构,如何操作才能满足这种需求呢?
答案是,使用队列,因为队列具有先进先出的特点,符合题解的情况。先将根结点push进去,从第二层开始,每次将data中上一层存入的元素都pop出去,每pop一个元素,就将该元素(树的结点)的左孩子右孩子push到data中(孩子为空,跳过)。这样就可以让data在遍历过程中保存每一层的结点了,我们也可以借机打印每层结点的值了。
接下来我们就可以开始写程序了。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
vector<vector<int> >result;
vector<vector<int> > Print(TreeNode* pRoot) {
if(pRoot==NULL) return result;
queueval);
if(last_layer_node->left)
layer_nodes.push(last_layer_node->left);
if(last_layer_node->right)
layer_nodes.push(last_layer_node->right);
}
result.push_back(layer_prints);
}
return result;
}
}; 按之字形顺序打印二叉树
同上,只是从上到下遍历到偶数层时,将layer_prints反转一下。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
vector<vector<int> >result;
vector<vector<int> > Print(TreeNode* pRoot) {
if(pRoot==NULL) return result;
queueval);
if(last_layer_node->left)
layer_nodes.push(last_layer_node->left);
if(last_layer_node->right)
layer_nodes.push(last_layer_node->right);
}
if(layer_idx%2==0)
reverse(layer_prints.begin(), layer_prints.end());
result.push_back(layer_prints);
}
return result;
}
}; 从上往下打印二叉树
同上,只是不用分层打印了,更简单
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector<int> PrintFromTopToBottom(TreeNode* root) {
vector<int> result;
if(root==NULL) return result;
queueval);
layer_nodes.pop();
if(top->left)
layer_nodes.push(top->left);
if(top->right)
layer_nodes.push(top->right);
}
}
return result;
}
}; 序列化与反序列化二叉树
序列化与反序列二叉树是一个互相可逆的过程。序列化是将一棵树转化一个载有符合二叉树所需信息的字符串;反序列化,是根据字符串重新生成一棵同样的二叉树。
大致分析一下:
在设想序列化二叉树的方法时,首先需要考虑到从字符串恢复一颗二叉树需要什么信息。
- 我们需要所有结点的val值
- 还要记录二叉树值所在的位置
我们可以采取某种遍历顺序将结点的val转为字符串依次排放(不要跳过空结点存,它空结点存为为字符串’NULL’,这样是为了保持每个结点都有左右两个孩子的一致性结构,相当于将二叉树伪造成满二叉树,这可以简化对结构信息的存储)。由于val转为int后长度时多少char不确定,因此需要为每个每个结点的值之间设定一个分隔符,这里我们设为’,’。
反序列化时,按照序列化时遍历的顺序重新构造一棵同样的二叉树即可。
接下来我们借助实例,具体分析一下:

- 序列化的过程就是:给定了一棵二叉树,层序遍历它,并在遍历过程中将val转为字符串并加上一个’,’
- 反序列化的过程就是:给定一个字符串,从左到右遍历它,将’,’分割的结点值重新转为int(如果字符串’NULL’说明时空结点),并层序遍历构造二叉树。
接下来我们就可以开始写程序了。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
string serialStr;
TreeNode* deserialRoot;
char* Serialize(TreeNode *root) {
queueif(last_layer_node)
layer_vals_str += to_string(last_layer_node->val);
else
layer_vals_str += "NULL";
layer_vals_str += ",";
if(last_layer_node)
layer_nodes.push(last_layer_node->left);
if(last_layer_node)
layer_nodes.push(last_layer_node->right);
}
serialStr += layer_vals_str;
}
return const_cast<char*>(serialStr.c_str());
}
TreeNode* Deserialize(char *str) {
int offset = 0;
deserialRoot = getValFromStr(str, offset);
queueif(node == NULL)
continue;
node->left = getValFromStr(str, offset);
node->right = getValFromStr(str, offset);
if(node->left)
layer_nodes.push(node->left);
if(node->right)
layer_nodes.push(node->right);
}
}
return deserialRoot;
}
TreeNode* getValFromStr(string str, int &offset)
{
// cout<<"offset:"<
for(int i=offset;i<(int)str.size();i++)
{
if(str[i]==',')
{
string val_str = str.substr(offset, i-offset);
offset = i+1;
// cout<<"val_Str:"<
if(val_str == "NULL")
return NULL;
else
return new TreeNode(stoi(val_str));
}
}
// for compile
return NULL;
}
}; 测试:
#include result;
if(root == NULL) return;
queue
for(int i=0;icout <val<<" ";
layer.pop();
if(top->left)
layer.push(top->left);
if(top->right)
layer.push(top->right);
}
cout<// for(int i=0;i
}
class Solution
{
...
};
int main()
{
TreeNode *root = NULL;//new TreeNode(4);
TreeNode *p2 = new TreeNode(2);
TreeNode *p3 = new TreeNode(5);
TreeNode *p4 = new TreeNode(1);
TreeNode *p5 = new TreeNode(3);
root->left = p2;
root->right = p3;
p2->left = p4;
p2->right = p5;
Solution s;
cout<char* serialStr = s.Serialize(root);
printTree(s.Deserialize(serialStr));
return 0;
} 另一种思路:
上面我们使用层序遍历的顺序保存二叉树的信息,还可以使用深度遍历的方法,ac代码如下,可以对比分析一下:
// 所谓序列化指的是遍历二叉树为字符串;
// 所谓反序列化指的是依据字符串重新构造成二叉树。
// 依据前序遍历序列来序列化二叉树,因为前序遍历序列是从根结点开始的。当在遍历二叉树时碰到Null指针时,这些Null指针被序列化为一个特殊的字符“#”。
// 另外,结点之间的数值用逗号隔开。
class Solution
{
public:
char* Serialize(TreeNode* root)
{
string serialStr;
SerializeHelper(root, serialStr);
char* serialChar = new char[serialStr.size()+1];
strcpy(serialChar, serialStr.c_str());
return serialChar;
}
void SerializeHelper(TreeNode* root, string &serialStr)
{
if(root==NULL)
{
serialStr+="#,";
return;
}
serialStr+=to_string(root->val);
serialStr+=",";
SerializeHelper(root->left, serialStr);
SerializeHelper(root->right, serialStr);
}
TreeNode* Deserialize(char* str)
{
string serialStr = str;
vector<string> splits = split(serialStr);
int idx = 0;
return DeserializeHelper(splits, idx);
}
TreeNode* DeserializeHelper(vector<string> eles, int &idx)
{
if(eles[idx]=="#")
return NULL;
TreeNode* root = new TreeNode(atoi(eles[idx].c_str()));
idx++;
root->left = DeserializeHelper(eles, idx);
idx++;
root->right = DeserializeHelper(eles, idx);
return root;
}
vector<string> split(const string& serialStr)
{
cout<vector<string> splits;
int lastIdx = 0;
for(int i=0;iif(serialStr[i]==',')
{
// cout<<"@"<
splits.push_back(serialStr.substr(lastIdx, i-lastIdx));
lastIdx = i+1;
}
}
return splits;
}
}; 二叉树中和为某一值的路径
路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。如何进行遍历?如何在遍历过程中记录路径的长度?
先大致分析一下:
这种从根节点到叶结点的遍历路径和我们递归深度遍历树的时候的遍历顺序是一样的,因此遍历方式就选择深度遍历,这里我们选择其中的先序遍历。我们向下一层时,将结点值加到path中,遍历到叶子结点时比较该路径长度是否与期待值相等。向上一层时(递归函数中与递归关联的code下面的区域,也就是在回溯的部分中),将该结点的值从path中去掉(有点像回溯算法中的恢复原来的值)。
比较清晰了,可以直接开始写代码了。
class Solution {
public:
vector<vector<int> > result;
vector<int> onePath;
vector<vector<int> > FindPath(TreeNode* root,int expectNumber) {
Traverse(root,expectNumber);
return result;
}
void Traverse(TreeNode* root, int expectNumber)
{
if(root==NULL) return;
onePath.push_back(root->val);
if(root->left==NULL && root->right ==NULL)
{
int sum = 0;
for(int i=0; iif(sum == expectNumber)
result.push_back(onePath);
}
Traverse(root->left, expectNumber);
Traverse(root->right, expectNumber);
onePath.pop_back();
}
}; 二叉树的深度
二叉树的深度是指值,树的最长路径。有两种解法:
1. 层序遍历,求层数
2. 深度遍历,求最长路径长度
很简单,直接写code
1.
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
int TreeDepth(TreeNode* pRoot)
{
if(pRoot==NULL) return 0;
queue m_queue;
m_queue.push(pRoot);
int depth = 0;
while(!m_queue.empty())
{
for(int i=0;iif(top->left)
{
m_queue.push(top->left);
}
if(top->right)
{
m_queue.push(top->right);
}
}
depth++;
}
return depth;
}
}; 2.
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
int depth = 0;
vector<int> onePath;
int TreeDepth(TreeNode* pRoot)
{
if(pRoot==NULL) return 0;
Traverse(pRoot);
return depth;
}
void Traverse(TreeNode* root)
{
if(root==NULL) return;
onePath.push_back(root->val);
if(root->left==NULL && root->right ==NULL)
{
depth = depth > onePath.size()?depth:onePath.size();
}
Traverse(root->left);
Traverse(root->right);
onePath.pop_back();
}
};二叉搜索树的第k个结点
如何找出二叉搜索树的第k小的结点?二叉搜索树中结点顺序时怎样的?如何利用顺序规律找到第k个结点。
我们大致分析一下:
二叉搜索树具有任一结点一定比其左子树中每个结点大,比其右子树中每个结点小的特点。且其中序遍历结果是从小到大排序的。因此,找到第k小的结点,其实就是找中序遍历的第k个结点。
借助实例具体分析一下:

由于k值是一个任意给定的值(可能小于等于0,也可能大于搜索树中实际的结点个数),因此,我们可以先分析常规情况,然后对这些特殊情况进行处理。
0. 如果k<=0,第k小结点为NULL
1. 递归中序遍历搜索二叉树,第k小的结点就是遍历的k个结点
2. 如果结束遍历都没有返回结点,说明k大于搜索树中的结点个数,第k小的结点为NULL
接下来就可以写代码了。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
int idx;
TreeNode* KthNode(TreeNode* pRoot, int k)
{
if(pRoot == NULL || k<=0) return NULL;
idx = 0;
TreeNode* kthNode = NULL;
_MidOrder(pRoot, k, kthNode);
return kthNode;
}
void _MidOrder(TreeNode* pRoot, const int &k, TreeNode* &kthNode)
//注意,要在函数中改变指针的指向时,指针参数要加&,否则时函数中改变的指针的copy变量,且随着函数结束这个copy被销毁,传入的指针并没有被改变
{
if(pRoot == NULL) return;
_MidOrder(pRoot->left, k, kthNode);
idx++;
if(idx == k)
{
kthNode = pRoot;
return;
}
_MidOrder(pRoot->right, k, kthNode);
}
};如果MidOrder函数不想要这么多参数,可以将kthNode变量的声明提出函数外,声明为class的全局变量,就可以直接在成员函数无需传参直接修改它了。
class Solution {
public:
int idx;
TreeNode* kthNode = NULL;
TreeNode* KthNode(TreeNode* pRoot, int k)
{
if(pRoot == NULL || k<=0) return NULL;
idx = 0;
// TreeNode* kthNode = NULL;
_MidOrder(pRoot, k, kthNode);
return kthNode;
}
void _MidOrder(TreeNode* pRoot, const int &k)//, TreeNode* &kthNode)
//注意,要在函数中改变指针的指向时,指针参数要加&,否则时函数中改变的指针的copy变量,且随着函数结束这个copy被销毁,传入的指针并没有被改变
{
if(pRoot == NULL) return;
_MidOrder(pRoot->left, k, kthNode);
idx++;
if(idx == k)
{
kthNode = pRoot;
return;
}
_MidOrder(pRoot->right, k, kthNode);
}
};二叉搜索树与双向链表
如何将二叉搜索树转化为双向链表,二叉搜索树的左右指针指向有什么特定?左右指针在搜索树中的指向与双向链表的前驱后继结点有什么联系吗?
先大致分析一下:
二叉搜索树的中序遍历序列中的结点顺序和双向链表的结点顺序一致,如果在遍历过程中,将左右孩子指针的指向调整为双向链表期望的指向就搜索树转化为双向链表了。
接下来,我们借助实例具体分析一下,如何调整左右孩子指针的指向:
首先我们固定了遍历顺序为中序遍历,此外,我们要依次两两获取遍历序列中的相邻结点,这借助变量暂存前1个结点实现(不暂存后1结点的原因时,因为我们还没遍历到后1结点,因此无法获取,而前1结点由于已经遍历过可以轻易获得),以便调整left、right指针的目标值。

1. 从2开始(last_node为1),让last_node->right指向自己
2. 接下来调整3(last_node为2),让自己->left指向last_node
3. 接下来调整4(last_node为3),让last_node->right指向自己,自己->left指向last_node
4. 接下来调整5(last_node为4),让自己->left指向last_node
我们发现1234操作的规则是一样的,总结一下:
中序遍历二叉树,并在中序遍历的过程中调整指针,使得left指向中序的前一结点,中序的前一结点的right指向该结点
接下来就可以写代码了:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* lastVisit = NULL;
midOrder_convertToLink(pRootOfTree, lastVisit);
TreeNode* newHead = pRootOfTree;
if(newHead==NULL) return NULL;
while(newHead->left)
{
newHead = newHead->left;
}
return newHead;
}
// 中序遍历二叉树,并在中序遍历的过程中调整指针,使得left指向中序的前一结点,中序的前一结点的right指向该结点
void midOrder_convertToLink(TreeNode *root, TreeNode *&lastVisit)
{
if(root==NULL) return;
midOrder_convertToLink(root->left, lastVisit);
root->left = lastVisit;
if(lastVisit!=NULL) lastVisit->right = root;
lastVisit = root;
midOrder_convertToLink(root->right, lastVisit);
}
};