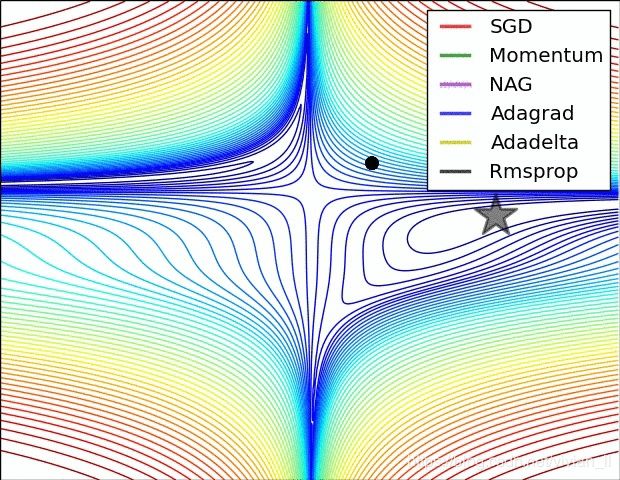
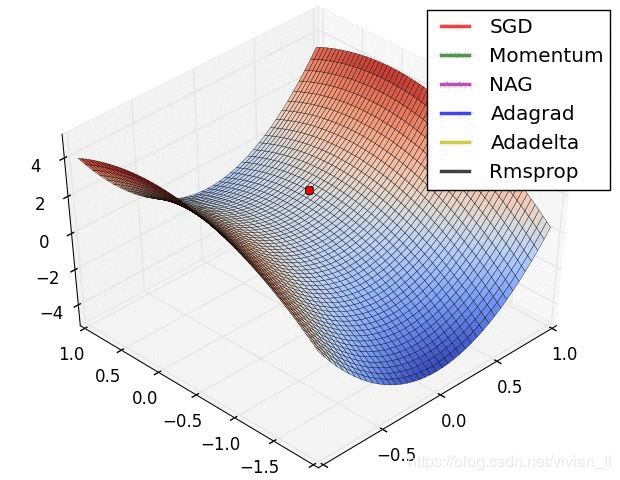
面试准备——机器学习中的优化器算法
一、优化问题
总体来看,机器学习的核心目标是给出一个模型(一般是映射函数),然后定义对这个模型好坏的评价函数(目标函数),求解目标函数的极大值或者极小值,以确定模型的参数,从而得到我们想要的模型。在这三个关键步骤中,前两个是机器学习要研究的问题,建立数学模型。第三个问题是纯数学问题,即最优化方法。
对于形式和特点各异的机器学习算法优化目标函数,我们找到了适合它们的各种求解算法。除了极少数问题可以用暴力搜索来得到最优解之外,我们将机器学习中使用的优化算法依照求解方法的不同,可以分成以下两类:解析解和数值解。
- 解析解给出一个最优化问题精确的公式解,所谓的解析解是一种包含分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式,也称为公式解,一般是理论结果。
- 数值解是在要给出极值点的精确计算公式非常困难的情况下,用数值计算方法近似求解得到最优点。
除此之外,还有其他一些求解思想,如分治法,动态规划等。
一般机器学习和深度学习中都是通过数值计算的方法近似得到最优解,以下方法多为数值解的角度。
二、驻点、鞍点与局部极值
首先来回顾一些优化算法相关的数学问题。
对于一个可导函数,寻找其极值的统一做法是寻找导数为0的点,即费马定理。微积分中的这一定理指出,对于可导函数,在极值点处导数必定为0:
f ′ ( x ) = 0 f^{\prime}(x)=0 f′(x)=0
对于多元函数,则是梯度为0:
∇ f ( x ) = 0 \nabla f(x)=0 ∇f(x)=0
导数为0的点称为驻点。需要注意的是,导数为0只是函数取得极值的必要条件而不是充分条件,它只是疑似极值点。是不是极值,是极大值还是极小值,还需要看更高阶导数。
对于一元函数,假设x是驻点:
-
如果 f ′ ′ ( x ) > 0 f^{\prime\prime}(x)>0 f′′(x)>0,则在该点处取极小值
-
如果 f ′ ′ ( x ) < 0 f^{\prime\prime}(x)<0 f′′(x)<0,则在该点处取极大值
-
如果 f ′ ′ ( x ) = 0 f^{\prime\prime}(x)=0 f′′(x)=0,还要看更高阶导数
海森矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,对函数 f ( x 1 , x 2 , . . . , x n ) f(x_1,x_2,...,x_n) f(x1,x2,...,xn),Hessian矩阵为:
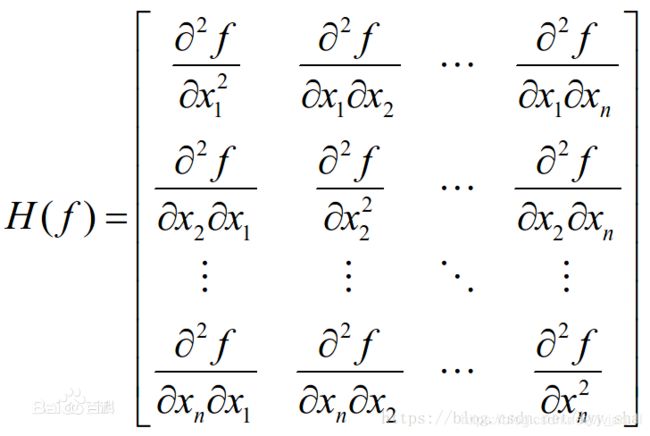
在导数为0的点处,函数可能不取极值,这称为鞍点。下图是鞍点的一个例子(来自SIGAI云端实验室):
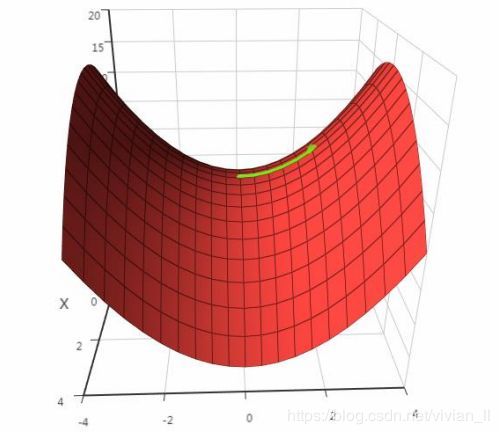
对于多元函数,假设x是驻点:
- 如果Hessian矩阵H正定, H ≻ 0 H \succ 0 H≻0(所有特征值> 0),那么二次型问题在高维空间中呈“碗”形,且严格凸(只有一个全局最小值)。如果 f ′ ( x ) = 0 f^{\prime}(x)=0 f′(x)=0,那么 x x x是全局最小值点。
- 如果半正定, H ⪰ 0 H\succeq 0 H⪰0(所有特征值>=0),则函数是凸的,如果 f ′ ( x ) = 0 f^{\prime}(x)=0 f′(x)=0,则 x x x是局部最小值点。
- 如果负正定 H ≺ 0 H\prec 0 H≺0(所有特征值<0),二次型问题在高维情况下呈倒碗状,并且是严格凹的(只有一个全局最大值)。如果 f ′ ( x ) = 0 f^{\prime}(x)=0 f′(x)=0,那么 x x x就是全局最大值。
- 如果半负定 H ⪯ 0 H⪯0 H⪯0(所有特征值< = 0),那么函数是凹的。如果 f ′ ( x ) = 0 f^{\prime}(x)=0 f′(x)=0,则 x x x是局部最大值。
- 如果H是不定的(在 x x x处的特征值有正有负),这意味着 x x x是局部最小&局部最大,因此 x x x是一个鞍点。
除鞍点外,最优化算法可能还会遇到另外一个问题:局部极值问题,即一个驻点是极值点,但不是全局极值。如果我们对最优化问题加以限定,可以有效的避免这两种问题。典型的是凸优化,它要求优化变量的可行域是凸集,目标函数是凸函数。但是机器学习大部分问题,都不是凸优化问题。
虽然驻点只是函数取得极值的必要条件而不是充分条件,但如果我们找到了驻点,再判断和筛选它们是不是极值点,比之前要容易多了。无论是理论结果,还是数值优化算法,一般都以找驻点作为找极值点的目标。对于一元函数,先求导数,然后解导数为0的方程即可找到所有驻点。对于多元函数,对各个自变量求偏导数,令它们为0,解方程组,即可达到所有驻点。幸运的是,在机器学习中,很多目标函数都是可导的,因此我们可以使用这套方法。
三、优化方法
3.1 梯度下降法
梯度下降最常见的三种变形 Batch Gradient Descent,Stochastic Gradient Descent,Mini-Batch Gradient Descent,这三种形式的区别就是取决于我们用多少数据来计算目标函数的梯度。
由于GD是机器学习最基础的优化方法,因此本文仅以SGD为例进行介绍。
随机梯度下降(SGD)
在这里SGD和mini batch gradient descent是同一个意思,抽取m个小批量(独立同分布)样本,通过计算他们的平均梯度均值。
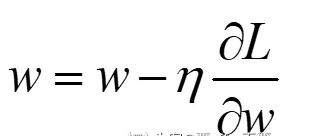
简单好理解,但是其存在的缺陷是,只有当自变量是一个维度的时候,它的前进方向才是真正梯度下降的方向。当存在多维变量时,若某一维度的梯度过大,会使得下降方向在该梯度方向的分量过大,偏离了真正的轨道。
优点:
- 针对大数据集,训练速度很快。从训练集样本中随机选取一个batch计算一次梯度,更新一次模型参数。
缺点:
- 选择恰当的初始学习率很困难。
- 学习率调整策略受限于预先指定的调整规则。
- 相同的学习率被应用于各个参数,如果我们的数据是稀疏的,我们更希望对出现频率低的特征进行大一点的更新。LR会随着更新的次数逐渐变小。leraning rate 选择太小,收敛速度会很慢,如果太大,则loss function会在极小值附近不停的震荡,甚至片偏离。
- 对于非凸函数,还要避免陷于局部极小值处,或者鞍点处,因为鞍点周围的error是一样的,所有维度的梯度都接近于0,SGD很容易被困在这里,即容易收敛到局部最优。
3.2 动量优化法
动量优化方法引入物理学中的动量思想,加速梯度下降,有Momentum和Nesterov两种算法。当我们将一个小球从山上滚下来,没有阻力时,它的动量会越来越大,但是如果遇到了阻力,速度就会变小,动量优化法就是借鉴此思想,使得梯度方向在不变的维度上,参数更新变快,梯度有所改变时,更新参数变慢,这样就能够加快收敛并且减少动荡。
Momentum(动量)
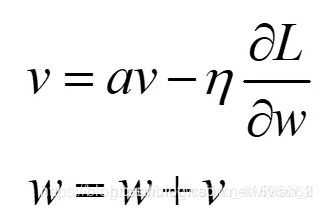
如果一直朝着某个方向前进,那么在这个方向上的梯度会越来越大。当使用SGD时,会出现过度振荡,徘徊前进,而在这个过程中其实那个梯度分量过大的方向的梯度其实在慢慢减小的,原本梯度分量较小的方向在慢慢增大,动量思想可以放大这个过程,使得模型尽快收敛。要是当前时刻的梯度与历史时刻梯度方向相似,这种趋势在当前时刻则会加强;要是不同,则当前时刻的梯度方式减弱,简言之就是通过积累之前的动量来加速当前的梯度。
特点:
- 下降初期时,使用上一次参数更新,下降方向一致,乘上较大的能够进行很好的加速。由于下降方向和梯度方向一致,而使t时刻的动量变大和t时刻的变化量变大,从而达到加速的目的
- 下降中后期时,在局部最小值来回震荡的时候, g r a d i e n t → 0 gradient\to0 gradient→0, μ \mu μ使得更新幅度增大,跳出陷阱
- 在梯度方向改变时,momentum能够降低参数更新速度,从而减少震荡;在梯度方向相同时,momentum可以加速参数更新, 从而加速收敛。总而言之,momentum能够加速SGD收敛,抑制震荡。
NAG(Nesterov)
momentum保留了上一时刻的梯度,对其没有进行任何改变,NAG(Nesterov accelerated gradient)是momentum的改进,在梯度更新时做一个矫正,具体做法就是在当前的梯度上添加上一时刻的动量,避免前进太快,同时提高灵敏度。 将上一节中的公式展开可得:
Δ θ t = − η ∗ μ ∗ m t − 1 − η ∗ g t \Delta{\theta_t}=-\eta*\mu*m_{t-1}-\eta*g_t Δθt=−η∗μ∗mt−1−η∗gt
可以看出,并没有直接改变当前梯度,所以Nesterov的改进就是让之前的动量直接影响当前的动量。即:
g t = ∇ θ t − 1 f ( θ t − 1 − η ∗ μ ∗ m t − 1 ) g_t=\nabla_{\theta_{t-1}}{f(\theta_{t-1}-\eta*\mu*m_{t-1})} gt=∇θt−1f(θt−1−η∗μ∗mt−1)
m t = μ ∗ m t − 1 + g t m_t=\mu*m_{t-1}+g_t mt=μ∗mt−1+gt
Δ θ t = − η ∗ m t \Delta{\theta_t}=-\eta*m_t Δθt=−η∗mt
所以,加上nesterov项后,梯度在大的跳跃后,进行计算对当前梯度进行校正。如下图:
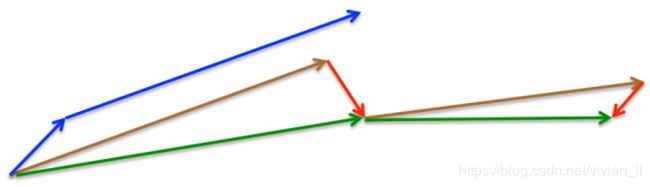
momentum首先计算一个梯度(短的蓝色向量),然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量),nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量),计算梯度然后进行校正(绿色梯向量)。
其实,momentum项和nesterov项都是为了使梯度更新更加灵活,对不同情况有针对性。但是,人工设置一些学习率总还是有些生硬,接下来介绍几种自适应学习率的方法。
3.3 自适应学习率优化算法
在机器学习中,学习率是一个非常重要的超参数,但是学习率是非常难确定的,虽然可以通过多次训练来确定合适的学习率,但是一般也不太确定多少次训练能够得到最优的学习率,玄学事件,对人为的经验要求比较高,所以是否存在一些策略自适应地调节学习率的大小,从而提高训练速度。
AdaGrad
AdaGrad,即Adaptive Gradient。

设置全局学习率之后,每次通过,全局学习率逐参数的除以历史梯度平方和的平方根,使得每个参数的学习率不同。
优点:学习率可以自适应的减小。
缺点:学习率过早、过量的减少。
Adadelta
Adadelta是对Adagrad的扩展,最初方案依然是对学习率进行自适应约束,但是进行了计算上的简化。 Adagrad会累加之前所有的梯度平方,而Adadelta只累加固定大小的项,并且也不直接存储这些项,仅仅是近似计算对应的平均值。即:
n t = ν ∗ n t − 1 + ( 1 − ν ) ∗ g t 2 n_t=\nu*n_{t-1}+(1-\nu)*g_t^2 nt=ν∗nt−1+(1−ν)∗gt2
Δ θ t = − η n t + ϵ ∗ g t \Delta{\theta_t} = -\frac{\eta}{\sqrt{n_t+\epsilon}}*g_t Δθt=−nt+ϵη∗gt
在此处Adadelta其实还是依赖于全局学习率的,但是作者做了一定处理,经过近似牛顿迭代法之后:
E ∣ g 2 ∣ t = ρ ∗ E ∣ g 2 ∣ t − 1 + ( 1 − ρ ) ∗ g t 2 E|g^2|_t=\rho*E|g^2|_{t-1}+(1-\rho)*g_t^2 E∣g2∣t=ρ∗E∣g2∣t−1+(1−ρ)∗gt2
Δ x t = − ∑ r = 1 t − 1 Δ x r E ∣ g 2 ∣ t + ϵ \Delta{x_t}=-\frac{\sqrt{\sum_{r=1}^{t-1}\Delta{x_r}}}{\sqrt{E|g^2|_t+\epsilon}} Δxt=−E∣g2∣t+ϵ∑r=1t−1Δxr
其中,E代表求期望。
此时,可以看出Adadelta已经不用依赖于全局学习率了。
特点:
- 训练初中期,加速效果不错,很快
- 训练后期,反复在局部最小值附近抖动
RMSProp
RMSProp,即Root Mean Square prop。
鉴于神经网络都是非凸条件下的,RMSProp在非凸条件下结果更好,改变梯度累积为指数衰减的移动平均以丢弃遥远的过去历史。
相比于AdaGrad的历史梯度:
![]()
RMSProp增加了一个衰减系数来控制历史信息的获取多少:
![]()

自适应调节学习率。对学习率进行了约束,适合处理非平稳目标和RNN。
Adam(重要)
Adam:Adaptive Moment Estimation
利用梯度的一阶矩估计和二阶矩估计动态调节每个参数的学习率。
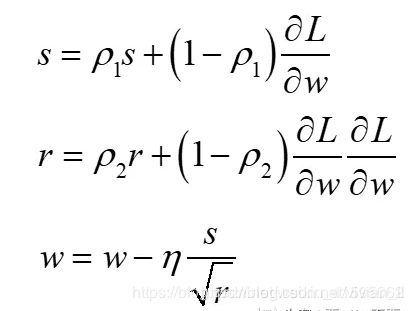
Adam算法可以看作修正后的Momentum+ RMSProp算法。

优点:
- 经过偏置校正后,每一次迭代都有确定的范围,使得参数比较平稳。善于处理稀疏梯度和非平稳目标。
- 对内存需求小
- 对不同内存计算不同的学习率
- 更新的步长能够被限制在大致的范围内(初始学习率)
- 能自然地实现步长退火过程(自动调整学习率)
- 很适合应用于大规模的数据及参数的场景
- 适用于不稳定目标函数
- 适用于梯度稀疏或梯度存在很大噪声的问题
Adam optimiser的局限性是什么?
虽然使用Adam进行训练有助于快速收敛,但结果模型的泛化性能往往不如使用SGD进行动量训练时的泛化性能。另一个问题是,即使Adam有自适应学习率,当使用良好的学习率计划时,它的性能也会提高。特别是在训练的早期,使用较低的学习率来避免发散是有益的。这是因为在一开始,模型的权值是随机的,因此得到的梯度不是很可靠。如果学习率太大,可能会导致模型采取太大的步骤,而没有确定合适的权重。当模型克服了这些初始稳定性问题后,可以提高学习速度,加快收敛速度。这个过程被称为学习率热身,其中一个版本在论文“Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour”中有描述。
AdamW和Adam有什么不同?
AdamW是Adam在权重上使用了L2正则化,这样小的权重泛化性能更好。
Adamax
Adamax是Adam的一种变体,此方法对学习率的上限提供了一个更简单的范围。公式上的变化如下:
n t = m a x ( ν ∗ n t − 1 , ∣ g t ∣ ) n_t=max(\nu*n_{t-1},|g_t|) nt=max(ν∗nt−1,∣gt∣)
Δ x = − m t ^ n t + ϵ ∗ η \Delta{x}=-\frac{\hat{m_t}}{n_t+\epsilon}*\eta Δx=−nt+ϵmt^∗η
可以看出,Adamax学习率的边界范围更简单。
Nadam
Nadam类似于带有Nesterov动量项的Adam。公式如下:
g t ^ = g t 1 − Π i = 1 t μ i \hat{g_t}=\frac{g_t}{1-\Pi_{i=1}^t\mu_i} gt^=1−Πi=1tμigt
m t = μ t ∗ m t − 1 + ( 1 − μ t ) ∗ g t m_t=\mu_t*m_{t-1}+(1-\mu_t)*g_t mt=μt∗mt−1+(1−μt)∗gt
m t ^ = m t 1 − Π i = 1 t + 1 μ i \hat{m_t}=\frac{m_t}{1-\Pi_{i=1}^{t+1}\mu_i} mt^=1−Πi=1t+1μimt
n t = ν ∗ n t − 1 + ( 1 − ν ) ∗ g t 2 n_t=\nu*n_{t-1}+(1-\nu)*g_t^2 nt=ν∗nt−1+(1−ν)∗gt2
n t ^ = n t 1 − ν t m t ˉ = ( 1 − μ t ) ∗ g t ^ + μ t + 1 ∗ m t ^ \hat{n_t}=\frac{n_t}{1-\nu^t}\bar{m_t}=(1-\mu_t)*\hat{g_t}+\mu_{t+1}*\hat{m_t} nt^=1−νtntmtˉ=(1−μt)∗gt^+μt+1∗mt^
Δ θ t = − η ∗ m t ˉ n t ^ + ϵ \Delta{\theta_t}=-\eta*\frac{\bar{m_t}}{\sqrt{\hat{n_t}}+\epsilon} Δθt=−η∗nt^+ϵmtˉ
可以看出,Nadam对学习率有了更强的约束,同时对梯度的更新也有更直接的影响。一般而言,在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。
3.4 牛顿法与拟牛顿法
牛顿法
牛顿法是二阶优化技术,也是求解无约束最优化问题的方法,收敛速度较快(考虑到了二阶导数的信息),利用了函数的一阶和二阶导数信息,直接寻找梯度为0的点。
我们假设点 x ∗ x^∗ x∗为函数 f ( x ) f(x) f(x)的根,那么有 f ( x ∗ ) = 0 f(x^∗)=0 f(x∗)=0。现在我们把函数 f ( x ) f(x) f(x)在点 x k x_k xk处一阶泰勒展开有:
f ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) f(x)=f(x_k)+f'(x_k)(x-x_k) f(x)=f(xk)+f′(xk)(x−xk)
假设点 x k + 1 x_{k+1} xk+1为该方程的根,则有:
f ( x k + 2 ) = f ( x k ) + f ′ ( x k ) ( x k + 1 − x k ) = 0 f(x_{k+2})=f(x_k)+f'(x_k)(x_{k+1}-x_k)=0 f(xk+2)=f(xk)+f′(xk)(xk+1−xk)=0
可以得到:
x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} xk+1=xk−f′(xk)f(xk)
这样我们就得到了一个递归方程,我们可以通过迭代的方式不断的让x趋近于x∗从而求得方程f(x)的解。
已经证明,如果 f ′ f' f′是连续的,并且待求的零点x是孤立的,那么在零点x周围存在一个区域,只要初始值x0位于这个邻近区域内,那么牛顿法必定收敛。 并且,如果 f ′ ( x ) f '(x) f′(x)不为0, 那么牛顿法将具有平方收敛的性能。粗略的说,这意味着每迭代一次,牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。
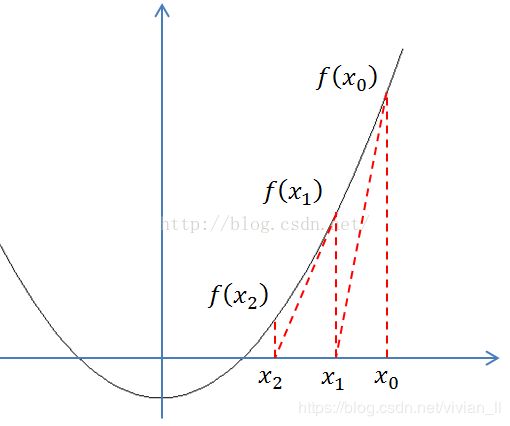
牛顿法的迭代公式为:
X k + 1 = X k − γ H k − 1 g k X_{k+1}=X_k-\gamma H^{-1}_kg_k Xk+1=Xk−γHk−1gk
或表示成:
d i = g ( θ i − 1 ) d_i=g(\theta_{i-1}) di=g(θi−1)
θ i = θ i − 1 − λ H i − 1 − 1 d i \theta_i=\theta_{i-1}-\lambda H^{-1}_{i-1}d_i θi=θi−1−λHi−1−1di
其中 H H H为Hessian矩阵, g k g_k gk为梯度向量。牛顿法不能保证每次迭代时函数值下降,也不能保证收敛到极小值点。在实现时,也需要设置学习率,原因和梯度下降法相同,是为了能够忽略泰勒展开中的高阶项。学习率的设置通常采用直线搜索(line search)技术。
在实现时,一般不直接求Hessian矩阵的逆矩阵,因为计算比较复杂,而是求解下面的线性方程组:
H k d = − g k H_kd=-g_k Hkd=−gk
其解d称为牛顿方向。迭代终止的判定依据是梯度值充分接近于0,或者达到最大指定迭代次数。
牛顿法比梯度下降法有更快的收敛速度,但每次迭代时需要计算Hessian矩阵,并求解一个线性方程组,运算量大。另外,如果Hessian矩阵不可逆,则这种方法失效。
牛顿法在logistic回归,AdaBoost算法等机器学习算法中有实际应用。
拟牛顿法
牛顿法在每次迭代时需要计算出Hessian矩阵,并且求解一个以该矩阵为系数矩阵的线性方程组,Hessian矩阵可能不可逆。为此提出了一些改进的方法,典型的代表是拟牛顿法。拟牛顿法的思路是不计算目标函数的Hessian矩阵然后求逆矩阵,而是通过其他手段得到一个近似Hessian矩阵逆的矩阵。具体做法是构造一个近似Hessian矩阵或其逆矩阵的正定对称矩阵,用该矩阵进行牛顿法的迭代。
拟牛顿法用一个矩阵 G G G来近似代替 H − 1 H^{-1} H−1(或 B B B来代替 H H H),其中 G G G满足拟牛顿条件:
G i + 1 y i = δ i ( B i + 1 δ i = y i ) G_{i+1}y_i=\delta_i(B_{i+1}\delta_i=y_i) Gi+1yi=δi(Bi+1δi=yi)
其中 y i = g ( θ i + 1 ) − g ( θ i ) y_i=g(\theta_{i+1})-g(\theta_i) yi=g(θi+1)−g(θi), δ i = x i + 1 − x i \delta_i=x_{i+1}-x_i δi=xi+1−xi。因此按照拟牛顿条件,每次只需更新 G i + 1 G_{i+1} Gi+1(或 B i + 1 B_{i+1} Bi+1)即可,使得 G i + 1 = G i + Δ G i G_{i+1}=G_i+\Delta G_i Gi+1=Gi+ΔGi。
牛顿法有多种的具体实现,其中DFP算法选择更新 G G G,BFGS选择更新 B B B,这里就不细讲了。
3.5 坐标轴下降法
坐标下降法的基本思想是每次对一个变量进行优化,这是一种分治法。坐标轴下降法和梯度下降法具有同样的思想,都是沿着某个方向不断迭代,但是梯度下降法是沿着当前点的负梯度方向进行参数更新,而坐标轴下降法是沿着坐标轴的方向。
假设要求解的优化问题为:
m i n f ( x ) , x = ( x 1 , x 2 , . . . , x n ) T min f(x),x=(x_1,x_2,...,x_n)^T minf(x),x=(x1,x2,...,xn)T
坐标下降法求解流程为每次选择一个分量 x i x_i xi进行优化,将其他分量固定住不动,这样将一个多元函数的极值问题转换为一元函数的极值问题,这样也避免了Lasso回归的损失函数不可导的问题。如果要求解的问题规模很大,这种做法能有效的加快速度。
坐标轴下降法等非梯度优化的方法可以解决L1正则化不可导的问题。
3.6 *NLP中大型预训练模型常用优化器
按照时间上的迭代顺序,近些年神经网络先后出现了 GD、Momentum、AdaGrad、RMSprop、Adam等上述优秀的优化器。到如今,大部分 NLP 预训练模型已不再使用这些方法,而是使用AdamW和去年首度亮相的 LAMB。
AdamW
AdamW即Adam Weight Decay Regularization
Adam虽然收敛速度快,但没能解决参数过拟合的问题。学术界讨论了诸多方案,其中包括在损失函数中引入参数的 L2 正则项。这样的方法在其他的优化器中或许有效,但会因为 Adam 中自适应学习率的存在而对使用 Adam 优化器的模型失效。AdamW 的出现便是为了解决这一问题,达到同样使参数接近于 0 的目的。具体的举措,是在最终的参数更新时引入参数自身:
m t = β 1 m t − 1 + ( 1 − β 1 ) Δ W m_t=\beta_1m_{t-1}+(1-\beta_1)\Delta W mt=β1mt−1+(1−β1)ΔW
v t = β 2 v t − 1 + ( 1 − β 2 ) Δ W 2 v_t=\beta_2v_{t-1}+(1-\beta_2)\Delta W^2 vt=β2vt−1+(1−β2)ΔW2
m t ^ = m t 1 − β 1 t \hat{m_t}=\frac{m_t}{1-\beta_1^t} mt^=1−β1tmt
v t ^ = v t 1 − β 2 t \hat{v_t}=\frac{v_t}{1-\beta_2^t} vt^=1−β2tvt
W t ← W t − 1 − α ( m t ^ v t ^ + ϵ + λ W t − 1 ) W_t\leftarrow W_{t-1}-\alpha\big(\frac{\hat{m_t}}{\sqrt{\hat{v_t}}+\epsilon}+\lambda W_{t-1}\big) Wt←Wt−1−α(vt^+ϵmt^+λWt−1)
λ \lambda λ即为权重衰减因子,常见的设置为 0.005/0.01。这一优化策略目前正广泛应用于各大预训练语言模型。
LAMB
LAMB即Layer-wise Adaptive Moments optimizer for Batching training,是 2019 年出现的一匹新秀。 LAMB 出现的目的是加速预训练进程,这个优化器也成为 NLP 社区为泛机器学习领域做出的一大贡献。在使用 Adam 和 AdamW 等优化器时,一大问题在于 batch size 存在一定的隐式上限,一旦突破这个上限,梯度更新极端的取值会导致自适应学习率调整后极为困难的收敛,从而无法享受增加的 batch size 带来的提速增益。LAMB 优化器的作用便在于使模型在进行大批量数据训练时,能够维持梯度更新的精度:
m t = β 1 m t − 1 + ( 1 − β 1 ) Δ W m_t=\beta_1m_{t-1}+(1-\beta_1)\Delta W mt=β1mt−1+(1−β1)ΔW
v t = β 2 v t − 1 + ( 1 − β 2 ) Δ W 2 v_t=\beta_2v_{t-1}+(1-\beta_2)\Delta W^2 vt=β2vt−1+(1−β2)ΔW2
r t = m t v t + ϵ r_t=\frac{m_t}{\sqrt{v_t}+\epsilon} rt=vt+ϵmt
W t ← W t − 1 − α ⋅ ϕ ( ∣ ∣ W t − 1 ∣ ∣ ∣ ∣ r t + λ W t − 1 ∣ ∣ ) ( r t + λ W t − 1 ) W_t\leftarrow W_{t-1}-\alpha\cdot\phi\big(\frac{||W_{t-1}||}{||r_t+\lambda W_{t-1}||}\big)(r_t+\lambda W_{t-1}) Wt←Wt−1−α⋅ϕ(∣∣rt+λWt−1∣∣∣∣Wt−1∣∣)(rt+λWt−1)
其中, ϕ \phi ϕ是一个可选择的映射函数,一种是 ϕ ( z ) = z \phi(z)=z ϕ(z)=z,另一种则为起到归一化作用的 ϕ ( z ) = min ( max ( z , γ l ) \phi(z)=\min(\max(z, \gamma_l) ϕ(z)=min(max(z,γl), γ u \gamma_u γu和 γ u \gamma_u γu为预先设定的超参数,分别代表参数调整的下界和上界。这一简单的调整所带来的实际效果非常显著。使用 AdamW 时,batch size 超过 512 便会导致模型效果大幅下降,但在 LAMB 下,batch size 可以直接提到 32,000 而不会导致精度损失。
由于在下游微调预训练模型时,通常无需过大的数据集,因而 LAMB 仅在预训练环节使用。遗憾的是,LAMB 在 batch size 512 以下时无法起到显著作用,目前只能作为大体量财团的工具。
总结
以上仅为面试中常见的优化器,给出这些算法的分类和它们之间的关系如下图:
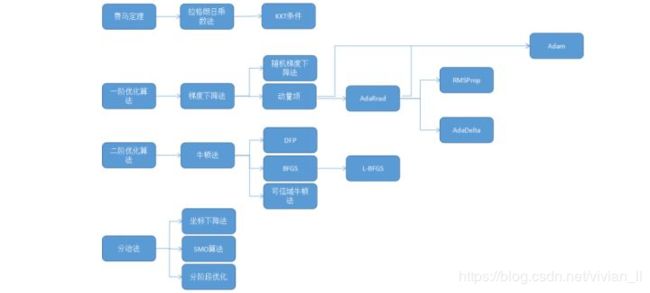
- 对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,而且最好采用默认值
- RMSprop, Adadelta, Adam 在很多情况下的效果是相似的
- 随着梯度变的稀疏,Adam 比 RMSprop 效果会好。
- SGD通常训练时间更长,但是在好的初始化和学习率调度方案的情况下,结果更可靠
- 如果在意更快的收敛,并且需要训练较深较复杂的网络时,推荐使用学习率自适应的优化方法。
- Adadelta,RMSprop,Adam是比较相近的算法,在相似的情况下表现差不多。
- 在想使用带动量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果
参考网址:
机器学习中优化算法总结(较多原理及图示)
深度学习几种优化器的比较(较全)
An overview of gradient descent optimization algorithms(很全,包含了SGD的一些变种)
机器学习各优化算法的简单总结(不全,但简单明了)
深度学习——优化器算法Optimizer详解(BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam)(较全,有动图)
坐标轴下降法(解决L1正则化不可导的问题)
AdamW, LAMB: 大型预训练模型常用优化器
机器学习中的最优化算法总结
牛顿法和拟牛顿法(原理讲解)
【机器学习】优化算法
最全的机器学习中的优化算法介绍