线性回归之最小二乘法

线性回归

线性回归是很常见的一种回归，线性回归可以用来预测或者分类，主要解决线性问题。

最小二乘法

线性回归过程主要解决的就是如何通过样本来获取最佳的拟合线。最常用的方法便是最小二乘法，它是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。

代数推导：

1. 假设拟合直线为 y=ax+b
2. 对任意样本点 (xi,yi)
3. 误差为 e=yi−(axi+b)
4. 当 S=∑ni=1ei2 为最小时拟合度最高，即 ∑ni=1(yi−axi−b)2 最小。
5. 分别求一阶偏导
   
   ∂S∂b=−2(∑i=1nyi−nb−a∑i=1nxi)

∂S∂a=−2(∑i=1nxiyi−b∑i=1nxi−a∑i=1nxi2)

6.分别让上面两式等于0，并且有 nx¯=∑ni=1xi ， ny¯=∑ni=1yi

7.得到最终解

a=∑ni=1(xi−x¯)(yi−y¯)∑ni=1(xi−x¯)2

b=y¯−ax¯

结果也可以如下

a=n∑xiyi−∑xi∑yin∑xi2−(∑xi)2

b=∑xi2∑yi−∑xi∑xiyin∑xi2−(∑xi)2

代码实现

import numpy as np
import matplotlib.pyplot as plt

def calcAB(x,y):
    n = len(x)
    sumX,sumY,sumXY,sumXX =0,0,0,0
    for i in range(0,n):
        sumX  += x[i]
        sumY  += y[i]
        sumXX += x[i]*x[i]
        sumXY += x[i]*y[i]
    a = (n*sumXY -sumX*sumY)/(n*sumXX -sumX*sumX)
    b = (sumXX*sumY - sumX*sumXY)/(n*sumXX-sumX*sumX)
    return a,b,

xi = [1,2,3,4,5,6,7,8,9,10]
yi = [10,11.5,12,13,14.5,15.5,16.8,17.3,18,18.7]
a,b=calcAB(xi,yi)
print("y = %10.5fx + %10.5f" %(a,b))
x = np.linspace(0,10)
y = a * x + b
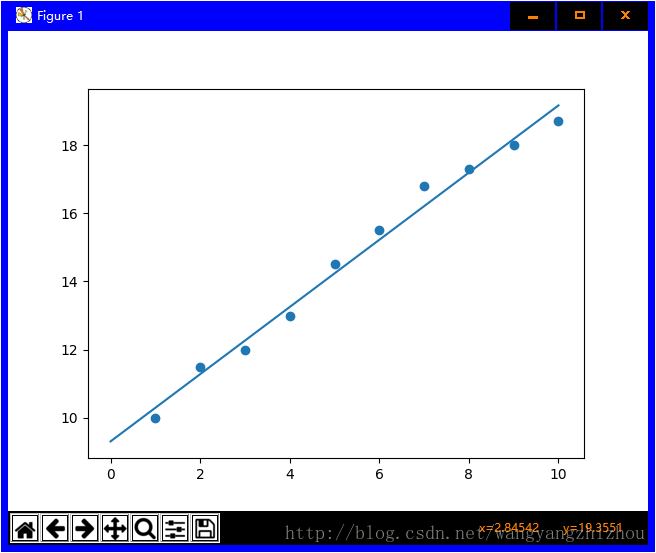
plt.plot(x,y)
plt.scatter(xi,yi)
plt.show()

运行结果

矩阵推导

1. 对于 y=ax+b 转为向量形式
   
   W=[w0w1]$‘，‘$X=[1x1]
2. 于是 y=w1x1+w0=WTX
3. 损失函数为
   
   L=1n∑i=1n(yn−(WTX)2)=1n(y−XW)T(y−XW)
   
   最后可化为

1nXTWTXW−2nXTWTy+1nyTy

1. 令偏导为0

∂L∂W=2nXTXW−2nXTy=0

另外， (XTX)−1XTX=E ， EW=W
则，

(XTX)−1XTXW=(XTX)−1XTy

W=(XTX)−1XTy

代码实现

import numpy as np
import matplotlib.pyplot as plt

x = [1,2,3,4,5,6,7,8,9,10]
y = [10,11.5,12,13,14.5,15.5,16.8,17.3,18,18.7]

A = np.vstack([x,np.ones(len(x))]).T

a,b = np.linalg.lstsq(A,y)[0]
print("y = %10.5fx + %10.5f" %(a,b))
x = np.array(x)
y = np.array(y)

plt.plot(x,y,'o',label='data',markersize=10)
plt.plot(x,a*x+b,'r',label='line')
plt.show()

运行结果

========广告时间========

公众号的菜单已分为“分布式”、“机器学习”、“深度学习”、“NLP”、“Java深度”、“Java并发核心”、“JDK源码”、“Tomcat内核”等，可能有一款适合你的胃口。

鄙人的新书《Tomcat内核设计剖析》已经在京东销售了，有需要的朋友可以购买。感谢各位朋友。

为什么写《Tomcat内核设计剖析》

=========================