9. 改变图像的对比度和亮度（OpenCV 官方文档翻译）

官方文档链接：https://docs.opencv.org/4.2.0/d3/dc1/tutorial_basic_linear_transform.html

---

目标 (Goal)

本教程学习：

• 访问像素值
• 用 0 初始化矩阵
• cv::saturate_cast 的作用
• 有关像素转换的信息
• 提高图像亮度的实例研究

---

理论 (Theory)

注意 (Note)

下面的理论解释来自 Richard Szeliski 的 《计算机视觉：算法与应用》 一书。

 

图像处理 (Image Processing)

• 一个通用的图像处理运算即是一个函数，它获取一个或多个输入图像并生成输出图像。
• 图像变换可以看作：
  • 点算子（像素变换）
  • 领域（基于区域）算子

---

像素变换 (Pixel Transforms)

• 在这种图像处理变换中，每个输出像素的值仅依赖于相应的输入像素值（加上一些可能全局收集的信息或参数）。
• 此类运算符的实例包括亮度和对比度调整以及颜色校正和转换。

---

亮度和对比度调整 (Brightness and contrast adjustments)

• 两个常用的点过程是带常数的乘法和加法：

$$g(x)=\alpha f(x)+\beta$$

• 参数 α>0 和 β 通常被称为 增益 和 偏置参数；有时这些参数被称为分别控制 对比度 和 亮度。
• 可以将 f(x) 是为源图像像素，将 g(x) 视为输出图像像素。然后，我们可以更方便地将表达式写成：

$$\begin{gathered} g(i,j)=\alpha \cdot f(i,j)+\beta \\ 其中i和j表示像素位于第i行和第j列中。 \end{gathered}$$

---

代码 (Code)

• 下面的代码执行的过程是

$$g(i,j)=\alpha \cdot f(i,j)+\beta$$

#include 

#include 
#include 
#include 
#include 

int main(int argc, char** argv)
{
	cv::Mat image = cv::imread(cv::samples::findFile("lena.jpg"));

	if (image.empty())
	{
		std::cout << "Could not open or find the image!\n" << std::endl;
		return -1;
	}

	cv::Mat new_image = cv::Mat::zeros(image.size(), image.type());

	double alpha = 1.0;		/*< Simple contrast control */
	int beta = 0;					/*< Simple brightness control */

	std::cout << " Basic Linear Transforms " << std::endl;
	std::cout << "----------------------------" << std::endl;
	std::cout << "* Enter the alpha value [1.0-3.0] : ";	std::cin >> alpha;
	std::cout << "* Enter the beta value [0-100] : ";		std::cin >> beta;

	for(int y = 0; y<image.rows; y++)
		for(int x = 0; x < image.cols; x++)
			for (int c = 0; c < image.channels(); c++)
			{
				new_image.at<cv::Vec3b>(y, x)[c] =
					cv::saturate_cast<uchar>(alpha * image.at<cv::Vec3b>(y, x)[c] + beta);
			}

	cv::imshow("Original Image", image);
	cv::imshow("New Image", new_image);

	cv::waitKey(0);
	return 0;
}

 

---

解释 (Explanation)

• 我们使用 cv::imread 加载图像并将其保存在 Mat 对象中：

    cv::Mat image = cv::imread(cv::samples::findFile("lena.jpg"));

	if (image.empty())
	{
		std::cout << "Could not open or find the image!\n" << std::endl;
		return -1;
	}

 

• 现在，因为我们将对这个图像进行一些转换，我们需要一个新的 Mat 对象来存储它。此外，我们也希望它具有以下功能：
  • 初始像素值等于 0
  • 与原始图像大小和类型相同

    cv::Mat new_image = cv::Mat::zeros(image.size(), image.type());

 

可以看到 cv::Mat::zeros 会基于 image.size() 和 image.type() 也就是图像的尺寸和类型返回一个 Matlab 风格的零初始值设定项。

• 然后要求用户输入 α 和 β 值：

	double alpha = 1.0;		/*< Simple contrast control */
	int beta = 0;					/*< Simple brightness control */

	std::cout << " Basic Linear Transforms " << std::endl;
	std::cout << "----------------------------" << std::endl;
	std::cout << "* Enter the alpha value [1.0-3.0] : ";	std::cin >> alpha;
	std::cout << "* Enter the beta value [0-100] : ";		std::cin >> beta;

 

• 现在，为了执行操作 g(i, j) = α · f(i, j) + β，我们将访问图像中的每个像素。由于我们使用的是 BGR 图像，因此每个像素有三个值 (B、G 和 R)，因此我们也将分别访问它们，代码如下：

    for(int y = 0; y<image.rows; y++)
    	for(int x = 0; x < image.cols; x++)
    		for (int c = 0; c < image.channels(); c++)
    		{
    			new_image.at<cv::Vec3b>(y, x)[c] =
    				cv::saturate_cast<uchar>(alpha * image.at<cv::Vec3b>(y, x)[c] + beta);
    		}

 

使用 C++ 编写代码时注意以下几点：

• 要访问图像中的每个像素，我们使用以下语法：image.atcv::Vec3b(y, x)[c]，其中 y 是行，x 是列，c 是 B、G 或 R（0、1 或 2）。
• 因为操作 α · p(i, j) + β 可以给出超出范围的值或不是整数（如果 α 是浮点数的话），因此我们使用 cv::saturate_cast 来确保这些值是有效的。
• 最后，我们创建窗口并以通常的方式显示图像。

	cv::imshow("Original Image", image);
	cv::imshow("New Image", new_image);

	cv::waitKey(0);

 

注意 (Note)

我们不必使用 for 循环来访问每个像素，只需使用以下命令：

    image.convertTo(new_image, -1, alpha, beta);

其中 cv::Mat::convertTo 将有效地执行 *new_image = α*image + β*。但是，之前的代码是想展示如何访问每个像素。无论如何，这两种方法都给出了相同的结果，但 convertTo 更优化，工作速度更快。

---

结果 (Result)

• 运行代码并使用 以下三组值：

α	β
1.5	30
2.5	30
2.5	50

• 得到的结果如下：

---

实例 (Practical example)

在这个部分，我们将把我们所学的通过调整图像的亮度和对比度来纠正曝光不足的图像的方法付诸实践。我们还将看到另一种校正图像亮度的技术，称为伽马校正。

 

亮度和对比度调整 (Brightness and contrast adjustments)

增大（或减小） β 值将为每个像素加上（或减去）一个常量值。超出 [0, 255] 范围的像素值将饱和（即高于（小于）255（0）的像素值）将被限制为 255（0）。

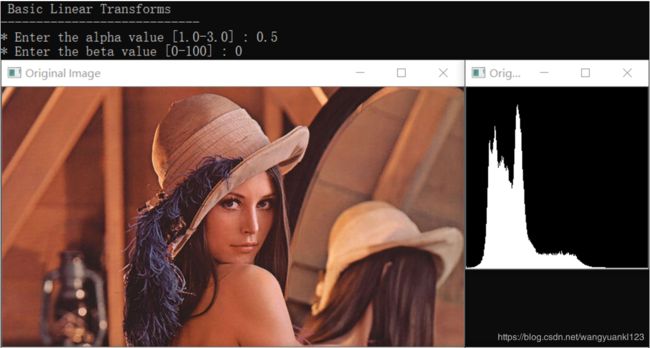
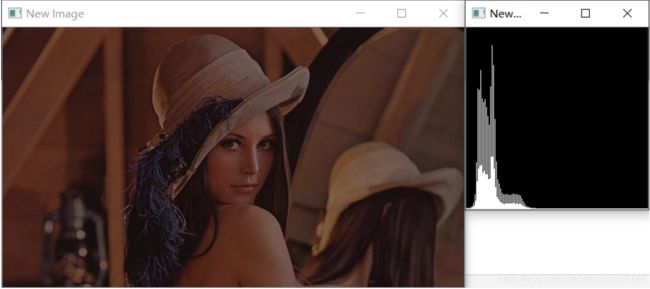
通过上述直方图可以看到当 α = 1，β = 80 时的源图像与转换后的图像以及各自的直方图。

直方图表示在图像中每个灰度级的像素个数。一幅深色的图像会有许多低颜色值的像素，因此直方图会在其左侧出现峰值。当添加一个恒定的偏移量时，即 β，直方图右移，因为我们已经向所有像素添加了一个恒定的偏移量。

 

α 参数将修改灰度级的扩散方式。如果 α < 1，则灰度级将被压缩，结果将是对比度较低的图像。

上图中，当 α = 0.5 时，变换之后的图像的直方图显示，灰度级被压缩了。

 

使用 β 偏置可以提高亮度，但同时随着对比度的降低，图像会出现轻微的面纱 （veil 不知道应该如何翻译，我理解的应该是图像会像是蒙上了一层薄雾一样的效果）。α 增益可以用来减小这种效应，但由于饱和，我们会丢失一些原始亮区的细节。

---

伽马校正 (Gamma correction)

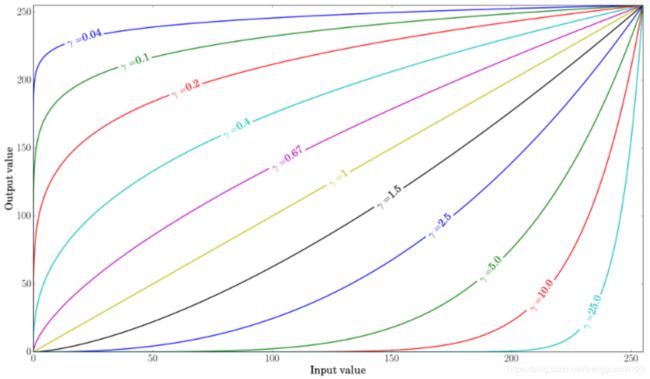
伽马校正可用于校正图像的亮度，方法是在输入值和映射输出值之间使用非线性变换：

$$O=(\frac{I}{255}{)}^{\gamma }\times 255$$

由于这种关系是非线性的，因此对所有像素的效果不尽相同，这也取决于它们的原始值。

当 γ < 1 时，原始的暗区将变亮，直方图右移；而 γ > 1 时则相反。

---

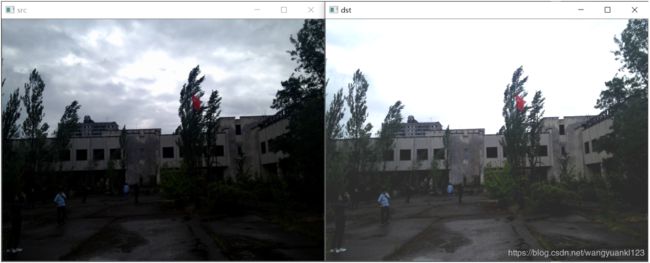
校正曝光不足的图像 (Correct an underexposed image)

一下图像已经校正为：α = 1.3 和 β = 40。结果如下：

 

整体亮度有所提高，但可以注意到，由于（摄影中的高光剪裁）数值饱和，云现在已经大大饱和，直接导致照片中的主体灰度级偏暗。

下面是用伽马校正对照片进行校正，选择 γ = 0.4。

由于映射是非线性的，并且不可能像以前的方法那样存在数值饱和，因此伽马校正只会增加较少的饱和效应。

上图比较了三幅图像的直方图。左图是 α β 校正之后的直方图，中间是原始图像的直方图，右侧是伽马校正后的直方图。可以注意到，大多数像素值位于原始图像直方图的下部。经过 α β 校正后，由于饱和而右移，可以看到在灰度级为 255 是会有一个大的峰值。经过伽马校正后，直方图向右移动，但暗区域中的像素比亮区域中的像素移动的更多。

---

在本教程中，可以看到两种简单的方法来调整图像的对比度和亮度。

---

代码 (Code)

伽马校正的代码：

    cv::Mat lookUpTable(1, 256, CV_8U);
    uchar* p = lookUpTable.ptr();
    for( int i = 0; i < 256; ++i)
        p[i] = cv::saturate_cast<uchar>(pow(i / 255.0, gamma_) * 255.0);
    cv::Mat res = img.clone();
    cv::LUT(img, lookUpTable, res);

查找表用于提高计算性能，只需要计算一次 256 个值。