机器学习问题总结(03)
文章目录
- 1.struct和class区别,你更倾向用哪个
- 2.kNN,朴素贝叶斯,SVM的优缺点,各种算法优缺点
- 2.1 KNN算法
- 2.2 朴素贝叶斯
- 2.3SVM算法
- 2.4 ANN算法
- 2.5 DT算法
- 3. 10亿个整数,1G内存,O(n)算法,统计只出现一次的数。
- 4、海量数据排序
- 4.1 数据库排序
- 4.2 分段排序
- 4.3 **bit位操作 **
- 5、项目中的数据是否会归一化处理,哪个机器学习算法不需要归一化处理
- 6、RBF核与高斯核的区别
- 7、L1和L2的区别
- 7.1 L1正则化
- 7.2 L2正则化
- 8、有哪些聚类方法?
- 8.1 常用聚类算法:
- 8.2 K-means聚类
- 8.3 层次聚类
- 9、什么是模糊聚类,还有划分聚类,层次聚类等
- 10、哪些模型容易过拟合,模型怎么选择
- 10.1 出现过拟合
- 10.2 模型选择方法
- 11、CART、GBDT
- 11.1 KNN(分类与回归)
- 11.2 CART
- 11.3 Logistics(推导)
- 11.4 GBDT
- 11.5 RF
- 12、写SVM的优化形式,用拉格朗日公式推导SVM kernel变换
- 13、数据结构当中的树,都有哪些
- 14、二分查找算法,递归、非递归实现,分析时间复杂度
- 15、几个排序算法,必须写出(快排)
- 15.1 快速排序
1.struct和class区别,你更倾向用哪个
结构与类共享几乎所有相同的语法,但结构比类受到的限制更多:
1、尽管结构的静态字段可以初始化,结构实例字段声明还是不能使用初始值设定项。
2、结构不能声明默认构造函数(没有参数的构造函数)或析构函数。
3、结构的副本由编译器自动创建和销毁,因此不需要使用默认构造函数和析构函数。实际上,编译器通过为所有字段赋予默认值(参见默认值表)来实现默认构造函数。结构不能从类或其他结构继承。
4、结构是值类型——如果从结构创建一个对象并将该对象赋给某个变量,变量则包含结构的全部值。
结构具有以下特点:
- 结构是值类型,而类是引用类型。
- 向方法传递结构时,结构是通过传值方式传递的,而不是作为引用传递的。
- 与类不同,结构的实例化可以不使用 new 运算符。
- 结构可以声明构造函数,但它们必须带参数。
- 一个结构不能从另一个结构或类继承,而且不能作为一个类的基。
- 所有结构都直接继承自 System.ValueType,后者继承自 System.Object。
- 结构可以实现接口。
- 在结构中初始化实例字段是错误的
2.kNN,朴素贝叶斯,SVM的优缺点,各种算法优缺点
2.1 KNN算法
KNN算法非常简单而且非常有效。 KNN的模型用整个训练数据集表示。 是不是特简单?
通过搜索整个训练集内K个最相似的实例(邻居),并对这些K个实例的输出变量进行汇总,来预测新的数据点。 对于回归问题,新的点可能是平均输出变量,对于分类问题,新的点可能是众数类别值。
成功的诀窍在于如何确定数据实例之间的相似性。如果你的属性都是相同的比例,最简单的方法就是使用欧几里德距离,它可以根据每个输入变量之间的差直接计算。
优点:
- 简单、有效。
- 重新训练的代价较低
- 计算时间和空间 线性于 训练集的规模
- 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
- 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
缺点:
- KNN算法是懒散学习方法(lazy learning,基本上不学习),一些积极学习的算法要快很多。
- 类别评分不是规格化的(不像概率评分)。
- 输出的可解释性不强,例如决策树的可解释性较强。
- 该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
- 计算量较大。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本
2.2 朴素贝叶斯
朴素贝叶斯是一种简单但极为强大的预测建模算法。
该模型由两种类型的概率组成,可以直接从你的训练数据中计算出来:1)每个类别的概率; 2)给定的每个x值的类别的条件概率。 一旦计算出来,概率模型就可以用于使用贝叶斯定理对新数据进行预测。 当你的数据是数值时,通常假设高斯分布(钟形曲线),以便可以轻松估计这些概率。
朴素贝叶斯被称为朴素的原因,在于它假设每个输入变量是独立的。 这是一个强硬的假设,对于真实数据来说是不切实际的,但该技术对于大范围内的复杂问题仍非常有效。
优点:
- 朴素贝叶斯模型发源于古典数学理论,有着坚实的数学基础,以及稳定的分类效率。
- NBC模型所需估计的参数很少,对缺失数据不太敏感,算法也比较简单
缺点:
- 理论上,NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为NBC模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的(可以考虑用聚类算法先将相关性较大的属性聚类),这给NBC模型的正确分类带来了一定影响。在属性个数比较多或者属性之间相关性较大时,NBC模型的分类效率比不上决策树模型。而在属性相关性较小时,NBC模型的性能最为良好。
- 需要知道先验概率。
- 分类决策存在错误率
2.3SVM算法
支持向量机也许是最受欢迎和讨论的机器学习算法之一。
超平面是分割输入变量空间的线。 在SVM中,会选出一个超平面以将输入变量空间中的点按其类别(0类或1类)进行分离。在二维空间中可以将其视为一条线,所有的输入点都可以被这条线完全分开。 SVM学习算法就是要找到能让超平面对类别有最佳分离的系数。
超平面和最近的数据点之间的距离被称为边界,有最大边界的超平面是最佳之选。同时,只有这些离得近的数据点才和超平面的定义和分类器的构造有关,这些点被称为支持向量,他们支持或定义超平面。在具体实践中,我们会用到优化算法来找到能最大化边界的系数值。在小数据集上可以表现比较好
优点:
- 可以解决小样本情况下的机器学习问题。
- 可以提高泛化性能。
- 可以解决高维问题。
- 可以解决非线性问题。
- 可以避免神经网络结构选择和局部极小点问题。
缺点: - 对缺失数据敏感。
- 对非线性问题没有通用解决方案,必须谨慎选择Kernel function来处理。
2.4 ANN算法
优点:
- 分类的准确度高
- 并行分布处理能力强,分布存储及学习能力强
- 对噪声神经有较强的鲁棒性和容错能力
- 能充分逼近复杂的非线性关系,具备联想记忆的功能等。
缺点: - 神经网络需要大量的参数,如网络拓扑结构、权值和阈值的初始值;
- 不能观察之间的学习过程,输出结果难以解释,会影响到结果的可信度和可接受程度;
- 学习时间过长,甚至可能达不到学习的目的
2.5 DT算法
决策树是机器学习的一种重要算法。
决策树模型可用二叉树表示。对,就是来自算法和数据结构的二叉树,没什么特别。 每个节点代表单个输入变量(x)和该变量上的左右孩子(假定变量是数字)
决策树学习速度快,预测速度快。 对于许多问题也经常预测准确,并且你不需要为数据做任何特殊准备。
优点:
- 决策树易于理解和解释.人们在通过解释后都有能力去理解决策树所表达的意义。
- 对于决策树,数据的准备往往是简单或者是不必要的.其他的技术往往要求先把数据一般化,比如去掉多余的或者空白的属性。
- 能够同时处理数据型和常规型属性。其他的技术往往要求数据属性的单一。
- 决策树是一个白盒模型。如果给定一个观察的模型,那么根据所产生的决策树很容易推出相应的逻辑表达式。
- 易于通过静态测试来对模型进行评测。表示有可能测量该模型的可信度。
- 在相对短的时间内能够对大型数据源做出可行且效果良好的结果。
- 可以对有许多属性的数据集构造决策树。
- 决策树可很好地扩展到大型数据库中,同时它的大小独立于数据库的大小。
缺点:
- 对于那些各类别样本数量不一致的数据,在决策树当中,信息增益的结果偏向于那些具有更多数值的特征。
- 决策树处理缺失数据时的困难。
- 过度拟合问题的出现。
- 忽略数据集中属性之间的相关性。
3. 10亿个整数,1G内存,O(n)算法,统计只出现一次的数。
4、海量数据排序
4.1 数据库排序
将文本文件导入到数据库,让数据库进行索引排序操作后提取数据到文件
优点:操作简单
缺点:运算速度慢,而且需要数据库设备。
4.2 分段排序
操作方式:
规定一个内存大小,比如200M,200M可以记录(20010241024/4) = 52428800条记录,我们可以每次提取5000万条记录到文件进行排序,要装满9位整数需要20次,所以一共要进行20次排序,需要对文件进行20次读操作
缺点:
编码复杂,速度也慢(至少20次搜索)
关键步骤:
先将整个9位整数进行分段,亿条数据进行分成20段,每段5000万条
在文件中依次搜索05000万,500000011亿……
将排序的结果存入文件
4.3 **bit位操作 **
思考下面的问题:
一个最大的9位整数为999999999
这9亿条数据是不重复的
可不可以把这些数据组成一个队列或数组,让它有0~999999999(10亿个)元素
数组下标表示数值,节点中用0表示这个数没有,1表示有这个数
判断0或1只用一个bit存储就够了
声明一个可以包含9位整数的bit数组(10亿),一共需要10亿/8=120M内存
把内存中的数据全部初始化为0, 读取文件中的数据,并将数据放入内存。比如读到一个数据为341245909这个数据,那就先在内存中找到341245909这个bit,并将bit值置为1遍历整个bit数组,将bit为1的数组下标存入文件
5、项目中的数据是否会归一化处理,哪个机器学习算法不需要归一化处理
一般基于梯度下降的算法都需要进行归一化处理
量纲问题:归一化有利于优化迭代速度(梯度下降),提高精度(KNN)
SVM需要归一化
LDA、DT 不需要归一化
6、RBF核与高斯核的区别
7、L1和L2的区别
7.1 L1正则化
- 计算绝对值之和,用以产生稀疏性,因为它是L0范式的一个最优凸近似,容易优化求解
- L1优点是能够获得sparse模型,对于large-scale的问题来说这一点很重要,因为可以减少存储空间。缺点是加入L1后目标函数在原点不可导,需要做特殊处理。可以做特征筛选
7.2 L2正则化
- 计算平方和再开根号,L2范数更多是防止过拟合,并且让优化求解变得稳定很快速(这是因为加入了L2范式之后,满足了强凸)
- L2优点是实现简单,能够起到正则化的作用。缺点就是L1的优点:无法获得sparse模型。实际上L1也是一种妥协的做法,要获得真正sparse的模型,要用L0正则化。
8、有哪些聚类方法?
8.1 常用聚类算法:
- K-means聚类
- 层次聚类
- SOM聚类(SOM神经网络)
- FCM聚类
- 谱聚类
- 模糊聚类
8.2 K-means聚类
**优点: **
简单直接,易于理解,在低维数据集上有不错的效果。
缺点:
对于高维数据,其计算速度十分慢,主要是慢在计算距离上,它的另外一个缺点就是它需要我们设定希望得到的聚类数k,若我们对于数据没有很好的理解,那么设置k值就成了一种估计性的工作。
8.3 层次聚类
优点:
1,距离和规则的相似度容易定义,限制少;
2,不需要预先制定聚类数;
3,可以发现类的层次关系(在一些特定领域如生物有很大作用);
缺点:
1,计算复杂度太高(考虑并行化);
2,奇异值也能产生很大影响;
3,算法很可能聚类成链状(一层包含着一层);
9、什么是模糊聚类,还有划分聚类,层次聚类等
模糊聚类分析一般是指根据研究对象本身的属性来构造模糊矩阵,并在此基础上根据一定的隶属度来确定聚类关系,即用模糊数学的方法把样本之间的模糊关系定量的确定,从而客观且准确地进行聚类。
聚类就是将数据集分成多个类或簇,使得各个类之间的数据差别应尽可能大,类内之间的数据差别应尽可能小,即为“最小化类间相似性,最大化类内相似性”原则 。
10、哪些模型容易过拟合,模型怎么选择
10.1 出现过拟合
- 决策树
- 神经网络
- KNN
10.2 模型选择方法
从训练集划分点数据出来形成验证集来近似测试误差;
对训练误差进行某种转化来近似测试误差。

11、CART、GBDT
11.1 KNN(分类与回归)
- 分类:取K近邻中所属类别数最多的那个类别
- 回归:取K近邻中所有样本的平均值最为该样本的预测值
11.2 CART
- 回归树用平方误差最小化准则
- 分类树用基尼指数最小化准则
11.3 Logistics(推导)
11.4 GBDT
- 利用损失函数的负梯度在当前模型的值作为回归问题提升树算法中的残差的近似值,拟合一个回归树
11.5 RF
- Bagging+CART
12、写SVM的优化形式,用拉格朗日公式推导SVM kernel变换
- SVM 凸优化问题
- 拉格朗日对偶(min和max交换顺序得到对偶问题)
引入拉格朗日因子
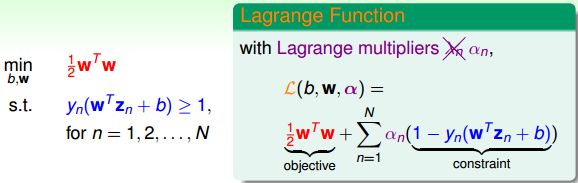
最小化问题中,包含着最大化问题,对偶后得到
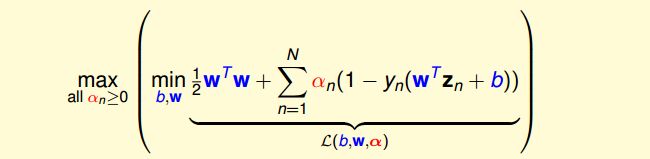
求导=0,带入后得到(被称为KKT条件)
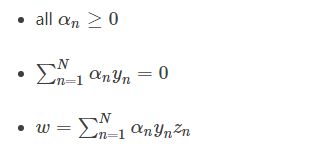
SVM最佳化形式转化为只与αn有关
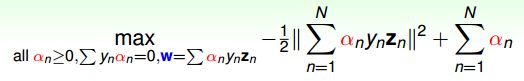
其中,满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT)
13、数据结构当中的树,都有哪些
二叉树、满二叉树、完全二叉树、二叉排序树、平衡二叉树
B树、B+树、红黑树、键树、字典树、区间树与线段树、败者树与胜者树
14、二分查找算法,递归、非递归实现,分析时间复杂度
#include
using namespace std;
/*
二分查找思想:
1、数组从小到大排序;
2、查找的key每次和中间数比较,如果key小于mid 查找mid左侧的数组部分;
如果key大于mid,则查找mid右侧的数组部分;如果相等,则直接返回mid。
输入:排序数组-array,数组大小-aSize,查找值-key
返回:返回数组中的相应位置,否则返回-1
*/
//非递归查找
int BinarySearch(int *array, int aSize, int key)
{
if (array == NULL || aSize == 0 )
return -1;
int low = 0;
int high = aSize - 1;
int mid = 0;
while ( low <= high )
{
mid = (low + high )/2;
if ( array[mid] < key)
low = mid + 1;
else if ( array[mid] > key )
high = mid - 1;
else
return mid;
}
return -1;
}
//递归
int BinarySearchRecursive(int *array, int low, int high, int key)
{
if ( low > high )
return -1;
int mid = ( low + high )/2;
if ( array[mid] == key )
return mid;
else if ( array[mid] < key )
return BinarySearchRecursive(array, mid+1, high, key);
else
return BinarySearchRecursive(array, low, mid-1, key);
}
int main()
{
int array[10];
for (int i=0; i<10; i++)
array[i] = i;
cout<<"No recursive:"< 15、几个排序算法,必须写出(快排)
15.1 快速排序
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
算法步骤:
1 从数列中挑出一个元素,称为 “基准”(pivot)
2 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
3 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。 递归的最底部情形,是数列的大小是0或1,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会退出,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
快速排序是基于分治模式处理的,对一个典型子数组A[p…r]排序的分治过程为三个步骤:
1.分解:
A[p…r]被划分为俩个(可能空)的子数组A[p …q-1]和A[q+1 …r],
使得 A[p …q-1] <= A[q] <= A[q+1 …r]
2.解决:
通过递归调用快速排序,对子数组A[p …q-1]和A[q+1 …r]排序。
3.合并。
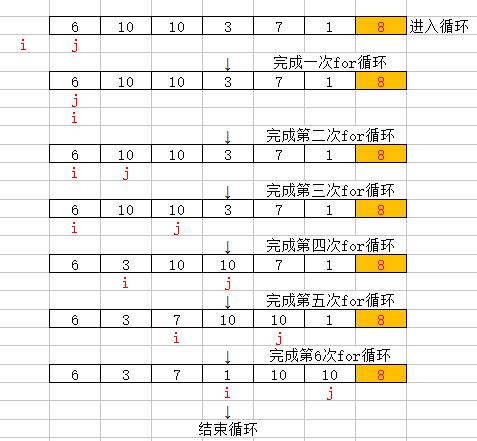
Partition过程:假设数组{6,10,10,3,7,1,8}
(1)从前都和8比较,6小于8,自己和自己交换,不变
(2)10大于8,不进入if
(3)10大于8,不进入if
(4)3小于8,交换到10之前
(5)7小于8,交换到10之前
(6)1小于8,交换到10之前
#include
using namespace std;
int Partition(int a[], int low, int high)
{
int x = a[high]; // 将输入数组的最后一个数作为主元,用它来对数组进行划分
int i = low - 1; // i是最后一个小于主元的数的下标
for (int j = low; j < high; j++) //遍历下标由low到high-1的数
{
if (a[j] < x) // 如果数小于主元的话就将i向前挪动一个位置
{ // 并且交换j和i所分别指向的数
int temp;
i++;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
// 经历上面的循环之后下标为从low到i(包括i)的数就均为小于x的数了
// 现在将主元和i+1位置上面的数进行交换
a[high] = a[i + 1];
a[i + 1] = x;
return i + 1;
}
void QuickSort(int a[], int low, int high)
{
if (low < high)
{
int q = Partition(a, low, high);
QuickSort(a, low, q - 1);
QuickSort(a, q + 1, high);
}
}
int main()
{
int buf[10] = { 12, 4, 34, 6, 8, 65, 3, 2, 988, 45 };
cout << "排序前:" << endl;
for(int i=0;i<10;i++)
cout << buf[i] <<" ";
QuickSort(buf, 0, 9);
cout << "\n\n排序后:" << endl;
for(int i=0;i<10;i++)
cout << buf[i] <<" ";
}
排序前: 12 4 34 6 8 65 3 2 988 45
排序后: 2 3 4 6 8 12 34 45 65 988