图卷积网络(GCN)简单理解

1. 预备知识

1.1 图网络的种类、区别和联系

Graph Embedding

Graph Embedding指图嵌入，属于表示学习的范畴，也可以称为网络嵌入、图表示学习、网络表示学习等等。

具体可以参考博主之前整理的关于图嵌入相关内容的资料：链接。

Graph Neural Network (GNN)

GNN指神经网络在图上应用的模型的统称，根据采用的技术不同和分类方法的不同，又可以分为很多不同种类。如从传播的方式来看，图神经网络可以分为图卷积网络（GCN），图注意力网络（GAT）等。

具体来说GNN指的是神经网络模型在图领域所用到的方法的统称。

Graph Convolutional Network

GCN属于GNN的一类，是采用卷积操作的图神经网络。这种方法属于一类采用图卷积的神经网络，可以应用于图嵌入的方法中。

上述三者的关系可以用下图来表示：

1.2 离散卷积

离散卷积本质就是一种加权求和。如下图所示，CNN中的卷积本质上就是一个共享参数的过滤器，通过计算中心像素点及相邻像素点的加权来构成feature map实现空间特征的提取。
其中卷积核的系数，通过随机化初值，然后根据loss反向传播梯度下降迭代优化。卷积核的函数通过优化求出才能实现特征提取的作用，GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。

1.3 为什么要研究GCN

CNN是计算机视觉领域的法宝，究其原因，是因为1.2中提到的，卷积核可以有效地提取出图像或视频数据中排列整齐的像素点矩阵，如下图所示。

相对应的，在科学研究中存在非欧式模型的数据，如下图所示，这是一个社交网络的数据结构。

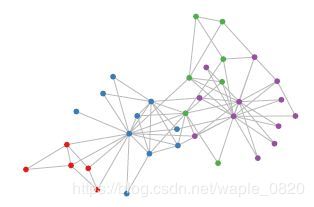
实际上，这样的网络结构就是图论中抽象意义上的拓扑图。所以，GCN中G代表用顶点和边建立相应关系的拓扑图。

研究GCN的主要原因有以下几点：

1. CNN无法处理Non Euclidean Structure的数据，学术上的表达是传统的离散卷积在这类数据上无法保持平移不变性。通俗讲就是在拓扑图中每个顶点的相邻顶点数目都可能不同，无法使用同样尺寸的卷积核来进行运算。
2. 我们希望在这种类似于拓扑图的结构上有效地提取空间特征来进行机器学习。
3. 广义上来说任何问题在赋范空间内都可以建立拓扑关联，谱聚类就是应用了这样的思想。这句话意思就是我们熟知的CV/NLP等问题实际上都可以通过建立拓扑关联转化为拓扑图的形式。所以说拓扑连接是一种广义的数据结构，GCN有很大的应用空间。

1.4 谱聚类

谱聚类（Spectral Clustering）是一种针对图结构的聚类方法，它跟其他聚类算法的区别在于，他将每个点都看作是一个图结构上的点，所以判断两个点是否属于同一类的依据就是，两个点在图结构上是否有边相连，可以是直接相连也可以是间接相连。举个例子，一个紧凑的子图（完全图）一定比一个松散的子图更容易聚成一类。

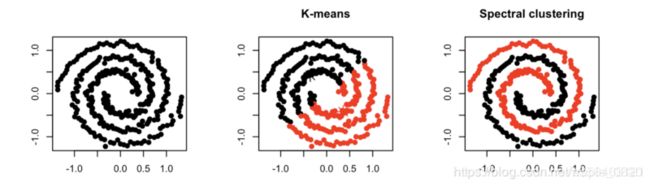
如上图，在k-means算法中会把空间分布距离较近的归为一类，而谱聚类则会把更紧凑的点聚为一类。

2. 图卷积预备定理

2.1 Motivation

图嵌入理论中我们说明了如果想把拓扑图转化为模型的输入，就必须将每个节点用其特征进行向量表示。而在试图得到节点表示的时候，容易想到的最方便的手段就是利用它周围的节点，也就是他的邻居节点等。

主要问题

1. 我们需要按照什么条件去找neighbors？
2. 确定感受野之后，按照什么方式处理包含不同数目的节点特征？

2.2 傅里叶变换

为了解决在拓扑图上无法有效地进行卷积计算的问题，我们需要了解Fourier变换的作用。

首先GCN中C(Convolution)的数学定义：
$$(f\ast g)(t)={\int }_{\Re }f(x)g(t-x)dx$$
一般称g为作用在f上的filter或kernel

根据卷积定理，卷积公式还可以写成： $$f\ast g={\mathcal{F}}^{-1}\{\mathcal{F}\{f\}\cdot \mathcal{F}\{g\}\}$$
这样我们只需要定义图上的傅里叶变换，就可以定义出图上的卷积变换。

到这里，我们首先需要推导上面的定理。

首先看看傅里叶变换的定义：
$$\mathcal{F}\{f\}(v)={\int }_{\Re }f(x)e^{-2\pi ix\cdot v}dx$$
其逆变换（Inverse Fourier）则是：
$${\mathcal{F}}^{-1}\{f\}(x)={\int }_{\Re }f(v)e^{2\pi ix\cdot v}dx$$

根据Fourier变换及其逆变换的定义，我们可以证明卷积定理。定义h是f和g的卷积，那么：
$$h(z)={\int }_{\Re }f(x)g(z-x)dx$$
有：
$$\begin{array}{rl}\mathcal{F}\{f\ast g\}(v)& =\mathcal{F}\{h\}(v)\\ & ={\int }_{\Re }h(z)e^{-2\pi iz\cdot v}dz\\ & ={\int }_{\Re }{\int }_{\Re }f(x)g(z-x)e^{-2\pi iz\cdot v}dxdz\\ & ={\int }_{\Re }f(x)({\int }_{\Re }g(z-x)e^{-2\pi iz\cdot v}dz)dz\end{array}$$
可以令$y=z-x;dy=dz$，得到：
$$\begin{array}{rl}\mathcal{F}\{f\ast g\}(v)& ={\int }_{\Re }f(x)({\int }_{\Re }g(y)e^{-2\pi i(y+x)\cdot v}dy)dx\\ & ={\int }_{\Re }f(x)e^{-2\pi ix\cdot v}({\int }_{\Re }g(y)e^{-2\pi iy\cdot v}dy)dx\\ & ={\int }_{\Re }f(x)e^{-2\pi ix\cdot v}dx{\int }_{\Re }g(y)e^{-2\pi iy\cdot v}dy\\ & =\mathcal{F}\{f\}(v)\cdot \mathcal{F}\{g\}(v)\end{array}$$
最后等式两边同时作用${\mathcal{F}}^{-1}$，得到：
$$f\ast g={\mathcal{F}}^{-1}\{\mathcal{F}\{f\}\cdot \mathcal{F}\{g\}\}$$

2.3 Laplacian算子

一阶导数定义为：
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
laplacian算子简单来说就是二阶导数：
$$\Delta f(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-2f(x)+f(x-h)}{h^2}$$
在graph上，我们可以定义一阶导数为：
$$f_{\ast g}^{\prime }(x)=f(x)-f(y)$$
其中y是x的邻居节点

那么对应的Laplacian算子可以定义为：
$${\Delta }_{\ast g}{f}^{\prime }(x)=\sum _{y\sim x}f(x)-f(y)$$

定义$D$是$N\times N$的度数矩阵(degree matrix)
$$D(i,j)=\{\begin{array}{rl}{d}_i& ifi=j\\ 0& otherwise\end{array}$$

定义$A$为$N\times N$的邻接矩阵(adjacency matrix)
$$A(i,j)=\{\begin{array}{rl}1& if{x}_i\sim x_j\\ 0& otherwise\end{array}$$

这里的两个矩阵定义都可以参考2.4中的例子来理解。

那么拉普拉斯算子可以写成：
$$L=D-A$$
标准化之后可以得到：
$$L=I_N-D^{-1/2}A{D}^{-1/2}$$

定义Laplacian算子的目的是为了找到Fourier变换的基，比如传统的Fourier变换的基$e^{2\pi ix\cdot v}$就是Laplacian算法的一组特征向量：
$$\Delta e^{2\pi ix\cdot v}=\lambda e^{2\pi ix\cdot v}$$
其中$\lambda$是一个常数。

那么上面的Fourier基就是$L$矩阵的n个特征向量$U=[u_1,...,u_n]$，$L$可以分解为：
$$L=U\Lambda U^T$$
其中$\Lambda$是特征值组成的对角矩阵

	传统Fourier变换	Graph Fourier变换
Fourier变换基	$e^{-2\pi ixv}$	$U^T$
逆Fourier变换基	$e^{2\pi ixv}$	$U$
维度	$\infty$	点的个数$n$

那么Graph Fourier变换可以定义为：
$$\mathcal{G}\mathcal{F}\{f\}({\lambda }_l)=\sum _{i=1}^{n}f(i)u_l^{\ast }(i)$$

其中$fi$可以看做是作用在第$i$个点上的signal，用向量$x=(f(1)\dots f(n))\in {\Re }^n$来表示。$u_l^{\ast }$是$u_l$的对偶向量，$u_l^{\ast }$是矩阵$U^T$的第$l$行，$u_l$是矩阵$U$的第$l$行。

那么我们可以用矩阵形式来表示Graph Fourier变换：
$$\mathcal{G}\mathcal{F}\{x\}=U^{T}x$$
类似的，Inverse Graph Fourier变换定义为：
$$\mathcal{I}\mathcal{G}\mathcal{F}\hat{f}(i)=\sum _{l=0}^{n-1}\hat{f}({\lambda }_l)u_l(i)$$
它的矩阵形式表达为：
$$\mathcal{I}\mathcal{G}\mathcal{F}\{x\}=Ux$$

2.4 相关矩阵定义

图中拉普拉斯矩阵就是由度矩阵D-邻接矩阵A构造出的。

3. 推导Graph Convolution

首先我们可以根据2中推导的卷积定理：
$$f\ast g={\mathcal{F}}^{-1}\{\mathcal{F}\{f\}\cdot \mathcal{F}\{g\}\}$$
那么图的卷积公式可以表示为：
$$g\ast x=U(U^{T}g\cdot U^{T}x)$$
作为图卷积的filter函数$g$，我们希望具有很好的局部性。就像CNN模型里的filter一样，只影响到一个像素附近的像素。那么我们可以把$g$定义成一个laplacian矩阵的函数$g(L)$。

作用一次laplacian矩阵相当于在图上传播了一次邻居节点。进一步我们可以把$U^{T}g$看做是$g_{\theta }(\Lambda )$一个laplacian特征值的函数。

改写上面的图卷积公式，我们就可以得到论文SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS（链接）的公式：
$$g_{\theta }\ast x=U{g}_{\theta }{U}^{T}x=U{g}_{{\theta }^{\prime }}(\Lambda )U^{T}x$$
可以看到这个卷积计算的复杂度非常高，涉及到求Laplacian矩阵的特征向量，和大量的矩阵计算。下面我们考虑对filter函数做近似，目标是省去特征向量的求解：
$$g_{{\theta }^{\prime }}(\Lambda )\approx \sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\tilde{\Lambda })$$
其中$T_k$是Chebyshev多项式。这里可以把简单$g_{\theta }(\Lambda )$简单看成是$\Lambda$的多项式。

因为：
$$U{\Lambda }^k{U}^T=(U\Lambda U^T{)}^k=L^k$$
所以上面filter函数可以写成$L$的函数：
$$g_{{\theta }^{\prime }}(\Lambda )\approx \sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\tilde{L})$$
设定$K=1$，卷积公式可以简化为：
$$\begin{array}{rl}{g}_{{\theta }^{\prime }}\ast x& \approx \theta (I_N+L)x\\ & =\theta (I_N+D^{-1/2}A{D}^{-1/2})x\end{array}$$
令$\tilde{A}=A+I_N$，${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$可以得到：
$$g_{{\theta }^{\prime }}\ast x=\theta ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2})x$$
那么再加上激活层，我们就可以得到最终的GCN公式：
$$H^{l+1}=\sigma ({\tilde{D}}^{-1/2}\tilde{A}{\tilde{D}}^{-1/2}{H}^{(l)}{W}^{(l)})$$

以上。