【Paper Reading】【CVPR2020】加法网络：AdderNet

AdderNet: Do We Really Need Multiplications in Deep Learning?
作者团队： 北京大学 & 华为诺亚实验室

0.相关资源

论文地址：arvix （如果arvix速度过慢，推荐使用中科院的镜像链接：cn.arvix）
开源代码: github
知乎关于论文的讨论：

• 如何评价Reddit热议的论文AdderNet？
• 另一篇简评

1. TL; DR

这是一篇CVPR2020的论文，作者针对神经网络中大量的乘法的问题设计了修改思路，提出了一种新的加法网络结构AdderNet。

将卷积网络中的乘法规则变成加法，需要对网络中的多种规则进行修改：

• 使用L1距离作为各层卷积核与输入特征之间输出的计算方法，并详尽分析了这种近似方法对神经网络的影响。(详见3.2)
• 为AdderNet设计了一种改进的带正则梯度的反向传播算法。(详见3.3)
• 提出一种针对神经网络每一层数量级不同的适应性学习率调整策略。(详见3.4)

实验结果表明，在ImageNet上使用ResNet-50可以达到SOTA的效果。但作者并没有给出实际运行时间或运行效率的对比结果。

2. Motivation

我们都知道，在计算机的计算单元里，浮点数的乘法计算复杂度比加法高得多，正式由于大量的乘法运算，也限制了它在移动设备上大规模使用的可能性。这是因为虽然GPU本身是一张卡中很小的一部分，但是仍然需要许多其他的硬件来支撑它的使用，如存储芯片、能源器件等，因此，神经网络需要尽可能地减少其计算开销。

对于这种思想，开创性的工作是Matthieu等人提出的二值网络¹，此后有众多学者提供了针对二值网络的参数优化改进方法。但是这些网络最大的问题就在于无法达到理想的效果，并且在训练的过程中无法保证稳定。

因此，作者希望设计一种基于加法的网络，在保证计算不包括乘法运算的同时减小二值网络中精度的损失。

3. Model

3.1. L1距离的可视化分析

作者首先讨论了使用L1距离的合理性。在对AdderNets和CNN的特征图可视化中（图1），可以看到CNN中不同的类别根据之间的角度进行区分（Softmax），而相反，在AdderNets中会根据类的中心点聚成一簇。这就说明了L1距离能够作为一个合适的指标去量化特征值和输入之间的距离。

图1. AdderNets和CNN的特征图可视化结果

3.2. Adder Networks

对于原始的CNN一层卷积运算，我们假定$F$是卷积核，$X$是输入特征，$Y$是输出特征，那么相互之间的计算关系可以表示为：
$$Y(m,n,t)=\sum _{i=0}^d\sum _{j=0}^d\sum _{k=0}^{c_{in}}S(X(m+i,n+j,k),F(i,j,k,t)),$$
其中$S(\cdot ,\cdot )$是一种定义好的相似性度量方法。如果是互相关函数(cross correlation)，则$S(x,y)=x\times y$，这个时候就是卷积的操作。

如果将这里的互相关替换成L1距离，那么上面的公式就变成了：
$$Y(m,n,t)=-\sum _{i=0}^d\sum _{j=0}^d\sum _{k=0}^{c_{in}}|X(m+i,n+j,k)-F(i,j,k,t)|,$$
其中的减法在运算中可以用补码的方式转化为加法，这样就能够得到不包含乘法运算的相似性度量方法。

这里需要注意的是，由于经过上述处理后的输出均为负数，作者把输出的结果过了一层BN，虽然这里的BN需要乘法运算，但是运算量相较于卷积中的运算可以忽略不计。

3.3. 优化方法

在CNN中，输出层对卷积核求偏导为：
$$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)}=X(m+i,n+j,k),$$
一般采用SGD去更新这些参数。

而在AdderNet中，这个偏导为：
$$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)}=sgn(X(m+i,n+j,k)-F(i,j,k,t)),$$
其中$sgn(\cdot )$是符号函数。

然而这个导数只能通过signSGD²进行更新，但signSGD会随着特征维数的增加而降低性能，并且永远不会沿着最陡的方向下降，并不适用于此。因此，作者采用了一种替代的方法(full-precision gradient)，即去掉外层$sgn(\cdot )$函数：
$$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)}=X(m+i,n+j,k)-F(i,j,k,t),$$
然而这样对输入特征$X$的梯度计算存在问题：如果使用full-precision gradient计算，那么在反向传播过程中，当每一级的梯度均大于+1或小于-1时，就会不可避免的造成梯度爆炸问题。因此，还需要对梯度的值进行约束。作者这里采用的方法是采用裁剪函数，当梯度值不在$[-1,+1]$范围内，就裁剪到边界值，即HardTanh函数：
$$HT(x)=\{\begin{array}{rl}& xif-1<x<1,\\ & 1x>1,\\ & -1x<-1.\end{array}$$
修改后的对输入特征的梯度变为：
$$\frac{\partial Y(m,n,t)}{\partial X(m+i,n+j,k)}=HT(F(i,j,k,t)-X(m+i,n+j,k)),$$

3.4. 学习率调整方法

首先通过对CNN和AdderNet的输出方差计算：
$$Var[Y_{CNN}]=\sum _{i=0}^d\sum _{j=0}^d\sum _{k=0}^{c_{in}}Var[X\times F]=d^2{c}_{in}Var[X]Var[F].$$

$$Var[Y_{AdderNet}]=\sum _{i=0}^d\sum _{j=0}^d\sum _{k=0}^{c_{in}}Var[|X-F|]=(1-\frac{2}{\pi })d^2{c}_{in}(Var[X]+Var[F]),$$
实际上$Var[F]$的值非常小，对普通的CNN大概在$10^{-3}$或$10^{-4}$这个量级，这样AdderNet的输出方差就远大于CNN的。

根据梯度传播的公式可以知道这时AdderNet的梯度远小于CNN的。作者在LeNet-5中测试两种网络的梯度大小，如图2所示。

图2. 第一次迭代每一层的梯度值

可以看到在AdderNet中卷积核的梯度远小于CNN中的，这可能会导致在训练AdderNet过程中参数更新过慢。

最直观的解决方法就是给AdderNets一个比较大的学习率，然而可以看到图2中，AdderNets的每一层梯度差距比较大，同样的速率可能不能适合所有的层，因此需要对每一层设定不同的学习率${\alpha }_l$，每一层更新的计算方法即：
$$\Delta F_l=\gamma \times {\alpha }_l\times \Delta L(F_l)，$$
其中$\gamma$是用于控制全局的学习率（如adder和BN层），$\Delta L(F_l)$是$l$层的梯度，并且类似于RMSProp中的学习率调整，采用的策略是根据卷积核$F_l$中梯度的L2正则：
$${\alpha }_l=\frac{\eta \sqrt{k}}{||\Delta L(F_l)|{|}_2}，$$
其中k是卷积核中元素的个数，用于平均L2正则的值，$\eta$是用于控制adder单元学习率的超参。

3.5. 算法流程

图3. 算法流程

4. Experiment

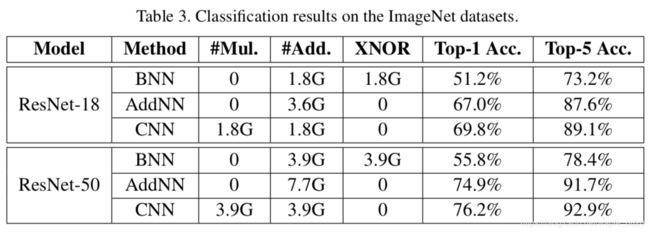
4.1. 分类任务上的性能对比

图4. 在CIFAR中分类的结果

图5. 在ImageNet任务上的准确率

从上面两个结果可以看到AdderNet在图像分类任务上可以在不做乘法运算（BN层忽略不计）基础上达到接近CNN的结果。

4.2. 可视化结果

图6. 两个不同网络在MNIST上第一层卷积核可视化的结果

可以看到虽然使用不同的距离度量指标，其中仍然有许多相似的特征模块，也证明了AdderNets能够很有效地从图像中提取信息。

除此之外，作者可视化了LeNet-5-BN网络中第三层参数的分布，如图7所示。

图7. AdderNet和CNN参数数值分布比较

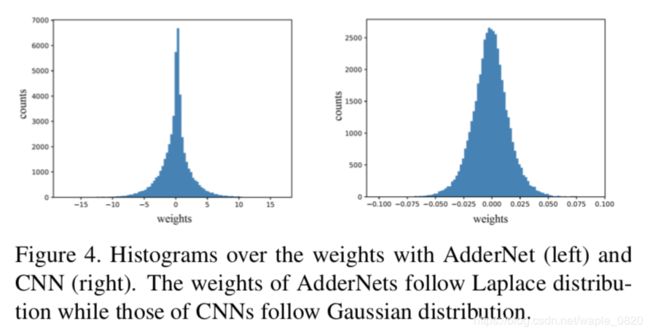
可以看到经过L1正则的AdderNet参数服从拉普拉斯分布(Laplace Distribution)，经过L2正则的CNN参数服从高斯分布(Gaussian Distribution)。

4.3. 消融实验

在这里作者讨论了求梯度的两种方法full-precision grad(FP)和sign grad(Sgn)，及学习率调整的两种方法Adaptive learning rate(ALR)和Increased learning rate(ILR)的训练情况，如图8所示。

图8. 对不同梯度计算方法和学习率调整方法的讨论

从上面的acc及loss的变化来看，ILR能够更快地让网络达到比较好的效果，但在训练后期会出现瓶颈无法提高，而ALR波动较大，但能随着epoch的增长达到更好的效果；梯度计算方法上，FP显著优于Sgn。

5. Thoughts

• 这篇文章突破了传统卷积需要大量乘法导致计算困难的问题，如果这种网络在大部分CV任务上都能够达到SOTA，就很有可能替代传统的乘法网络。

• 个人认为，本文中的一些优化的方法比较简单粗暴，比如对full-precision gradient可能会造成梯度爆炸问题的优化方法是直接采用HardTanh函数去裁剪。对这些问题的优化方法是否还可以挖掘更深的理论讨论空间？

• 另外，在Reddit论坛中讨论的比较厉害的一个问题就是本篇核心在于用加法来优化网络的运行效率，但是在结果中并没有给出实际的运行时间。不知道是作者疏忽了还是实际加法网络在现有的环境下依然有其他耗时瓶颈。

Reference

---

1. Matthieu Courbariaux, Yoshua Bengio, and Jean-Pierre David. Binaryconnect: Training deep neural networks with binary weights during propagations. In NeuriPS, pages
   3123–3131, 2015. ↩︎

2. Jeremy Bernstein, Yu-Xiang Wang, Kamyar Azizzade- nesheli, and Anima Anandkumar. signsgd: Compressed optimisation for non-convex problems. arXiv preprint arXiv:1802.04434, 2018. ↩︎