李航《统计学习方法》第四章——用Python实现朴素贝叶斯分类器（MNIST数据集）

相关文章:

• 李航《统计学习方法》第二章——用Python实现感知器模型（MNIST数据集）
• 李航《统计学习方法》第三章——用Python实现KNN算法（MNIST数据集）
• 李航《统计学习方法》第五章——用Python实现决策树（MNIST数据集）
• 李航《统计学习方法》第六章——用Python实现逻辑斯谛回归（MNIST数据集）
• 李航《统计学习方法》第六章——用Python实现最大熵模型（MNIST数据集）
• 李航《统计学习方法》第七章——用Python实现支持向量机模型（伪造数据集）
• 李航《统计学习方法》第八章——用Python+Cpp实现AdaBoost算法（MNIST数据集）
• 李航《统计学习方法》第十章——用Python实现隐马尔科夫模型

个人认为朴素贝叶斯比较适合特征维度较小的情况，但是MNIST数据已到达上百唯的特征,概率联乘起来超过Python float能表示的极限，因此需要一些trick来保证精度。

朴素贝叶斯

按照传统不详述该算法，具体内容可以看《统计学习方法》第四章。

这里只将书中算法贴出来

朴素贝叶斯认为所有特征都是独立的，然后得出一个样本出现的概率使其所有特征出现概率的联乘。

数据集

数据集没什么可以说的，和感知器模型那个博文用的是同样的数据集。

但这次我们可以多分类，因此用原始训练数据即可
数据地址：https://github.com/WenDesi/lihang_book_algorithm/blob/master/data/train.csv

特征

将整个图片作为特征

代码

这里要说明一下，由于Python 浮点数精度的原因，784个浮点数联乘后结果变为Inf，而Python中int可以无限相乘的，因此可以利用python int的特性对先验概率与条件概率进行一些改造。

先验概率： 由于先验概率分母都是N，因此不用除于N，直接用分子即可。
条件概率： 条件概率公式如下图所示，我们得到概率后再乘以10000，将概率映射到[0,10000]中，但是为防止出现概率值为0的情况，人为的加上1，使概率映射到[1,10001]中。

代码已放到Github上

#encoding=utf-8

import pandas as pd
import numpy as np
import cv2
import random
import time

from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score

# 二值化
def binaryzation(img):
    cv_img = img.astype(np.uint8)
    cv2.threshold(cv_img,50,1,cv2.cv.CV_THRESH_BINARY_INV,cv_img)
    return cv_img

def Train(trainset,train_labels):
    prior_probability = np.zeros(class_num)                         # 先验概率
    conditional_probability = np.zeros((class_num,feature_len,2))   # 条件概率

    # 计算先验概率及条件概率
    for i in range(len(train_labels)):
        img = binaryzation(trainset[i])     # 图片二值化
        label = train_labels[i]

        prior_probability[label] += 1

        for j in range(feature_len):
            conditional_probability[label][j][img[j]] += 1

    # 将概率归到[1.10001]
    for i in range(class_num):
        for j in range(feature_len):

            # 经过二值化后图像只有0，1两种取值
            pix_0 = conditional_probability[i][j][0]
            pix_1 = conditional_probability[i][j][1]

            # 计算0，1像素点对应的条件概率
            probalility_0 = (float(pix_0)/float(pix_0+pix_1))*1000000 + 1
            probalility_1 = (float(pix_1)/float(pix_0+pix_1))*1000000 + 1

            conditional_probability[i][j][0] = probalility_0
            conditional_probability[i][j][1] = probalility_1

    return prior_probability,conditional_probability

# 计算概率
def calculate_probability(img,label):
    probability = int(prior_probability[label])

    for i in range(len(img)):
        probability *= int(conditional_probability[label][i][img[i]])

    return probability

def Predict(testset,prior_probability,conditional_probability):
    predict = []

    for img in testset:

        # 图像二值化
        img = binaryzation(img)

        max_label = 0
        max_probability = calculate_probability(img,0)

        for j in range(1,10):
            probability = calculate_probability(img,j)

            if max_probability < probability:
                max_label = j
                max_probability = probability

        predict.append(max_label)

    return np.array(predict)


class_num = 10
feature_len = 784

if __name__ == '__main__':

    print 'Start read data'

    time_1 = time.time()

    raw_data = pd.read_csv('../data/train.csv',header=0)
    data = raw_data.values

    imgs = data[0::,1::]
    labels = data[::,0]

    # 选取 2/3 数据作为训练集， 1/3 数据作为测试集
    train_features, test_features, train_labels, test_labels = train_test_split(imgs, labels, test_size=0.33, random_state=23323)
    # print train_features.shape
    # print train_features.shape

    time_2 = time.time()
    print 'read data cost ',time_2 - time_1,' second','\n'

    print 'Start training'
    prior_probability,conditional_probability = Train(train_features,train_labels)
    time_3 = time.time()
    print 'training cost ',time_3 - time_2,' second','\n'

    print 'Start predicting'
    test_predict = Predict(test_features,prior_probability,conditional_probability)
    time_4 = time.time()
    print 'predicting cost ',time_4 - time_3,' second','\n'

    score = accuracy_score(test_labels,test_predict)
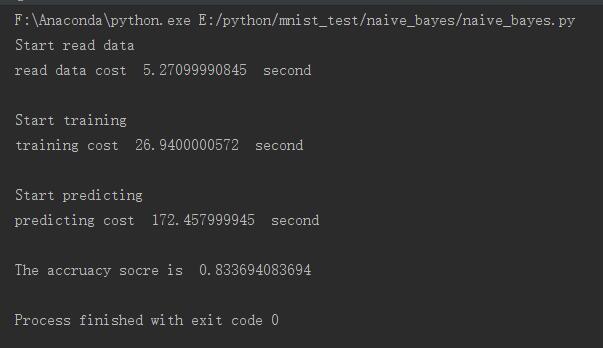
    print "The accruacy socre is ", score

运行结果如下所示
’

效果挺一般的，只有83%左右，比不上KNN，但运行时间要比KNN快的多