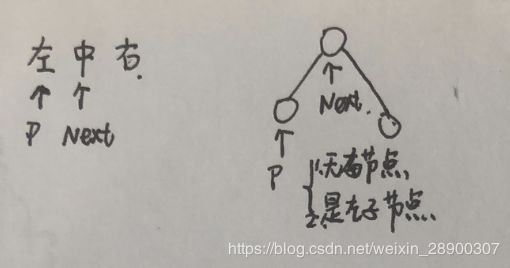
【前端js】实现剑指offer|leetcode(四)——二叉树题目集合
文章目录
- 一、遍历
- 1. 前序遍历
- 2. 中序遍历
- 3. 后序遍历
- 4. 二叉树的层序遍历
- 5. 二叉树的反向层序遍历
- 6.重建二叉树
- 二、深度/宽度
- 1. 二叉树的深度
- 三、查找节点
- 1. 二叉树的下一个结点
- 1. 二叉树的最近公共父节点
- 四、树的排序
- 1. 最大二叉树
- 五、树的路径
- 1. 二叉树中和为某一值的路径
- 2. 求根到叶子节点数字之和(leetcode 129. )
一、遍历
1. 前序遍历
leetcode 144. Binary Tree Preorder Traversal
https://leetcode.com/problems/binary-tree-preorder-traversal/
先访问根节点,再序遍历左子树,最后序遍历右子树

思路
和中序其他都相似,要先访问根节点要后访问左节点,所以在根节点入栈的时候加入result数组
- 特殊情况:根节点为空,返回空数组
- 利用
栈来存放访问过的根节点——定义一个指针指向要访问的节点,先访问根节点。将遍历到的结点值存入result数组,结点存入栈中。 - stack存放遍历过的根,左节点,
以便回溯访问右节点 - 然后指针一直向下访问
左节点 - 当根节点没有左节点时,将根节点退栈,然后指针指向
右节点,访问右节点 - 直到栈为空而且指针为空,所有节点遍历完成,退出循环,返回结果
var preorderTraversal = function(root) {
if (root === null) return []; //空树
var result = [],
stack = []; //result储存结果,stack存放遍历过的根,左节点,以便回溯访问右节点
var p = root; //p指向当前遍历的节点
//当有未访问的右节点(stack不空)||还有左节点没有访问(p不空)时进入循环
while (stack.length != 0 || p != null) {
//还有左节点没有访问(p不空)
if (p != null) {
result.push(p.val); //遍历根节点
stack.push(p); //把遍历过的节点放入stack保管
p = p.left; //访问左节点
}
//左节点访问完
else {
p = stack.pop().right; //栈顶节点退栈,访问右节点
}
}
return result;
};
2. 中序遍历
leetcode 94. Binary Tree Inorder Traversal
https://leetcode.com/problems/binary-tree-inorder-traversal/
先中序遍历左子树,再访问根节点,最后中序遍历右子树
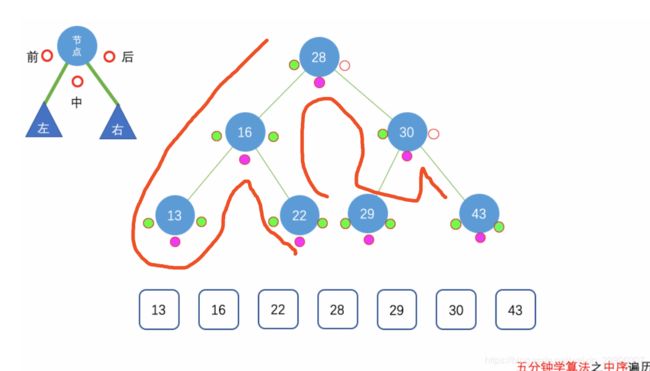
思路
和前序其他都相似,左节点要先访问根节点要后访问,所以在根节点出栈的时候加入result数组
- 特殊情况:根节点为空,返回空数组
- 利用
栈来存放访问过的根节点——定义一个指针指向要访问的节点,先访问根节点。,结点存入栈中。 - stack存放遍历过的根,左节点,
以便回溯访问右节点 - 然后指针一直向下访问
左节点 - 当根节点没有左节点时,将根节点退栈,将遍历到的
结点值存入result数组,然后指针指向右节点,访问右节点 - 直到栈为空而且指针为空,所有节点遍历完成,退出循环,返回结果
var inorderTraversal = function(root) {
if (root === null) return []; //空树
var result = [],
stack = []; //result储存结果,stack存放遍历过的根,左节点,以便回溯访问右节点
var p = root; //p指向当前遍历的节点
//当有未访问的右节点(stack不空)||还有左节点没有访问(p不空)时进入循环
while (stack.length != 0 || p != null) {
//还有左节点没有访问(p不空)
if (p != null) {
stack.push(p); //把遍历过的节点放入stack保管
p = p.left; //访问左节点
}
//左节点访问完
else {
let node = stack.pop();//栈顶节点退栈,
result.push(node.val); //遍历左节点-根节点
p = node.right; //访问右节点
}
}
return result;
};
3. 后序遍历
leetcode 94. Binary Tree Inorder Traversal
https://leetcode.com/problems/binary-tree-postorder-traversal/submissions/
先后序遍历左子树,再后序遍历右子树,最后访问根节点
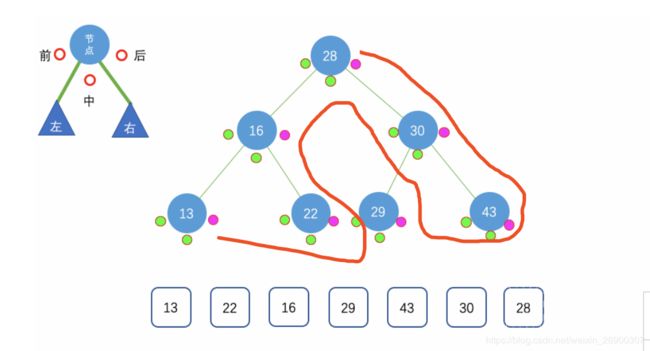
思路
和前序其他都相似,result数组要求顺序左节点-右节点-根节点
所以可以考虑从result头插入
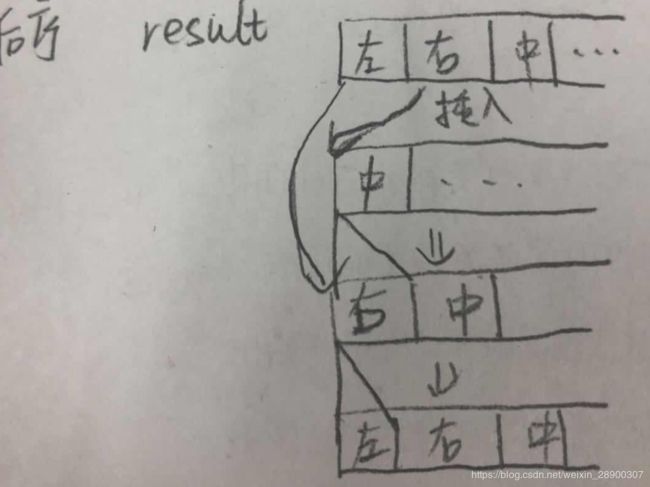
- 特殊情况:根节点为空,返回空数组
- 利用
栈来存放访问过的根节点——定义一个指针指向要访问的节点,先访问根节点。,结点存入栈中。 - stack存放遍历过的根,右节点,
以便回溯访问左节点 - 然后指针一直向下访问
右节点 - 当根节点没有右节点时,将根节点退栈,将遍历到的
结点值存入result数组,然后指针指向右节点,访问右节点 - 直到栈为空而且指针为空,所有节点遍历完成,退出循环,返回结果
var postorderTraversal = function(root) {
if (root === null) return []; //空树
var result = [],
stack = []; //result储存结果,stack存放遍历过的根,左节点,以便回溯访问右节点
var p = root; //p指向当前遍历的节点
//当有未访问的左节点(stack不空)||还有右节点没有访问(p不空)时进入循环
while (stack.length != 0 || p != null) {
//还有左节点没有访问(p不空)
if (p != null) {
stack.push(p); //把遍历过的节点放入stack保管
result.unshift(p.val); //从result数组头部插入根节点-右节点-左节点
//最后result顺序为左节点-右节点-根节点
p = p.right; //访问右节点
}
//右节点访问完
else {
p = stack.pop().left; //栈顶节点退栈,访问左节点
}
}
return result;
};
4. 二叉树的层序遍历
题目:
思路
- 特殊情况 ,根节点为null,深度为0,return 0
借助队列,队列储存每一层的所有节点,- 先
保存数组长度,用于控制依次遍历循环——遍历每一个节点保存值,该节点的所有子结点从队尾入队,访问过的节点从头出队 - 注意——需要先把
width存下来,用于for循环的结束标志,因为for循环里面直接操作了queue,不能去都不敢动态获取 - 队列初始值为
root,对每一层都要进行上述遍历——while循环控制,队列空代表叶节点这一层遍历完成,此时遍历结束,退出循环 - 每次循环开始前初始化一个
curNodes储存该层所有节点,每次循环结束,将curNodes压入result
var levelOrder = function(root) {
if (root === null) return []; //空树
var result = [],
queue = [root];
while (queue.length) {
let width = queue.length; //需要先把width存下来,用于for循环,for循环里面直接操作了数组
let curNodes = [];
for (let i = 0; i < width; i++) {
let node = queue.shift();
curNodes.push(node.val);
node.left ? queue.push(node.left) : "";
node.right ? queue.push(node.right) : "";
}
result.push(curNodes);
}
return result;
};
5. 二叉树的反向层序遍历
题目 给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
思路
- 参考正向层序遍历,改变结果数组的插入顺序即可
var levelOrderBottom = function(root) {
if (root === null) return []; //空树
var result = [],
queue = [root];
while (queue.length) {
let width = queue.length; //需要先把width存下来,用于for循环,for循环里面直接操作了数组
let curNodes = [];
for (let i = 0; i < width; i++) {
let node = queue.shift();
curNodes.push(node.val);
node.left ? queue.push(node.left) : "";
node.right ? queue.push(node.right) : "";
}
result.unshift(curNodes);//从头部插入,先插入顶部的,后插入底部的额
}
return result;
};
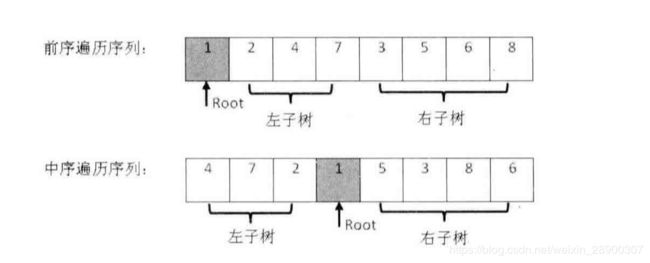
6.重建二叉树
题目 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。
思路
- 前序遍历:
根+左子树+右子树,中序遍历:左子树+根+右子树, - 根据规律,先从前序遍历第一个节点是
根节点,然后在中序遍历里定位这个节点,来划分前中序列,得到左右子树序列的前序+中序 递归法,每一次执行,只需要得到一个根节点和他的左右节点- 因此输入左子树的
前序+中序可以得到左子树的根节点,也就当前根节点的左节点,右边同理
特殊情况,前中序列有一个为空数组- 前序数组只有一个元素,说明是
叶节点,不需要找左右子树 - 前序数组只有多个元素,说明是
非叶节点,需要找左右子树——定位root,然后划分序列,递归调用输入划分的序列,得到左右子树
完整代码
function reConstructBinaryTree(pre, vin) {
if (pre.length === 0 || vin.length === 0) return null; // 前序/中序又一个为空,就返回空值
let root = new TreeNode(pre[0]); //新建节点,作为根节点
if (pre.length === 1) return root; //是叶节点直接返回root,不需要计算子树
//不是叶节点,先递归得到左右节点
let rootIdx = vin.indexOf(pre[0]); //根节点在中序的位置
root.left = reConstructBinaryTree(
// 递归调用得到左子树的根节点
pre.slice(1, rootIdx + 1),
vin.slice(0, rootIdx)
);
root.right = reConstructBinaryTree(
// 递归调用得到右子树的根节点
pre.slice(rootIdx + 1),
vin.slice(rootIdx + 1)
);
return root;
}
二、深度/宽度
1. 二叉树的深度
题目:
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
思路
- 特殊情况 ,根节点为null,深度为0,return 0
- 递归法,递归法获取左右子树的深度,
- root的深度是左右子树的深度最大值+1,返回深度
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
function TreeDepth(pRoot) {
// write code here
if (!pRoot) return 0; //根节点为空,深度为0
var left = TreeDepth(pRoot.left); //左深度等于左子树深度+1
var right = TreeDepth(pRoot.right); //右深度等于右子树深度+1
return 1 + Math.max(left, right); //该节点深度为左右深度中的max,返回
}
三、查找节点
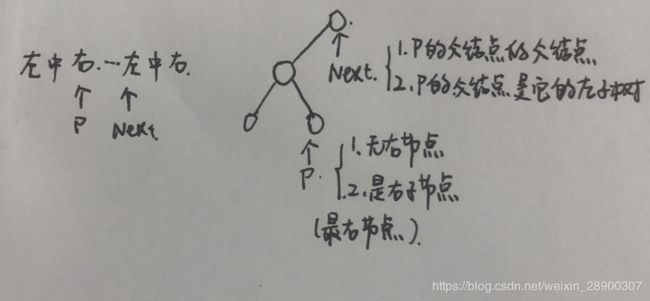
1. 二叉树的下一个结点
牛客网-剑指 offer-题目:
给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
思路
-
特殊情况空节点 -
情况三,没有右子结点,有父节点,当前节点是父节点的右节点,此时父节点一下都已经访问完,下一个访问父节点的父节点中,满足从左边连接的第一个
-
情况二和情况三可以归为一类——父节点存在时,设一个指针cur指向pnode父节点,- 如果pnode是cur的
左节点,返回; - 如果pnode是cur的
右节点,pnode向上指, - 如果退出循环,查找到根节点都
没有返回,就表示没有满足条件的节点,返回null
- 如果pnode是cur的
代码
function GetNext(pNode) {
// write code here
if (!pNode) return null; //空节点
var cur = null;
//有右节点,下一个访问右子树里的最左边节点
if (pNode.right) {
cur = pNode.right;
while (cur.left) {
cur = cur.left;
}
return cur;
}
//没有右节点,有父节点,
while (pNode.next) {
cur = pNode.next; //cur指向父节点
//如果pnode是cur的左节点,下一个访问的就是cur
if (cur.left === pNode) return cur;
//如果pnode不是cur的左节点,pnode指向父节点,向上继续查找
pNode = cur;
}
return null; //查找到根节点也没有符合条件的节点
}
1. 二叉树的最近公共父节点
leetcode-236. Lowest Common Ancestor of a Binary Tree:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
思路
递归法,拆分到每一个节点
特殊情况root为空节点,root等于q/p,此时父节点就是root

情况一,root的左右子树中均找到了p/q,此时父节点就是root情况二,root的左右子树中只有一个找到了p/q,此时父节点就是p/q-
情况三,root的左右子树中都没有找到了p/q,此时父节点就是p/q
情况二和情况三可以归为一类——父节点存在时,设一个指针cur指向pnode父节点,- 如果pnode是cur的
左节点,返回; - 如果pnode是cur的
右节点,pnode向上指, - 如果退出循环,查找到根节点都
没有返回,就表示没有满足条件的节点,返回null
- 如果pnode是cur的
代码
function GetNext(pNode) {
// write code here
if (!pNode) return null; //空节点
var cur = null;
//有右节点,下一个访问右子树里的最左边节点
if (pNode.right) {
cur = pNode.right;
while (cur.left) {
cur = cur.left;
}
return cur;
}
//没有右节点,有父节点,
while (pNode.next) {
cur = pNode.next; //cur指向父节点
//如果pnode是cur的左节点,下一个访问的就是cur
if (cur.left === pNode) return cur;
//如果pnode不是cur的左节点,pnode指向父节点,向上继续查找
pNode = cur;
}
return null; //查找到根节点也没有符合条件的节点
}
四、树的排序
1. 最大二叉树
题目:
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
二叉树的根是数组中的最大元素。
左子树是通过数组中最大值左边部分构造出的最大二叉树。
右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
思路
- 递归法实现构建二叉树
- 递归出口,数组长度为0,return null,返回空节点
- 根节点为传入数组的max值,
- 左节点为递归调用,传入以max为分割点的左边数组的返回值,
- 右节点为递归调用,传入以max为分割点的右边数组的返回值,
slice(left,right)分割数组,索引为left的元素划分进去,索引为right的元素不划分进去。
var constructMaximumBinaryTree = function(nums) {
if (nums.length <= 0) return null;
let max = Math.max(...nums);
let i = nums.indexOf(max);
let root = new TreeNode(max);
root.left = constructMaximumBinaryTree(nums.slice(0, i));
root.right = constructMaximumBinaryTree(nums.slice(i + 1));
return root;
};
五、树的路径
1. 二叉树中和为某一值的路径
题目:
输入一颗二叉树的跟节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
方法一:递归法
思路
- 因为要先访问最长的路径,所以考虑`
递归深度遍历:对根节点调用递归函数curPath保存当前路径,sum保存当前和,每访问一个节点,更新路径和和,- 更新之后,判断是否满足
叶节点+和为指定值,如果满足,压入结果数组 - 注意:因为
curPath是一个引用类型,它的值一直在变化,所以压入数组时需要先进行深拷贝,如果不拷贝会导致结果输出为最后的curPath空数组。 - 左右节点存在时,对左右节点递归遍历
- 当前节点和所有子节点遍历完成,当前节点退出路径
function FindPath(root, expectNumber) {
// write code here
if (!root) return [];
var res = [], //所有满足条件路径
curPath = [], //当前路径
p = root, //访问指针
sum = 0; //当前路径和
dfs(p, curPath, sum, res, (exp = expectNumber));
return res;
}
function dfs(p, curPath, sum, res, exp) {
if(!p&&curPath.length===0) return;//所有节点访问完毕,退出递归
curPath.push(p.val); //节点值加入路径
sum += p.val; //更新和
if (!p.left && !p.right && sum === exp) {
//栈顶节点是叶节点且路径满足条件
res.push(curPath.slice(0)); //路径加入结果
}
p.left ? dfs(p.left, curPath, sum, res, exp) : "";
p.right ? dfs(p.right, curPath, sum, res, exp) : "";
curPath.pop(); //节点和所有子树访问完毕,退出路径
}
方法二:非递归法
2. 求根到叶子节点数字之和(leetcode 129. )
题目:
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。例如,从根到叶子节点路径 1->2->3 代表数字 123。计算从根到叶子节点生成的所有数字之和。
方法一:递归法
思路
递归输入当前节点和上一层的和,初始为root和0- 如果节点空返回0
- 更新sum,是叶节点的话直接返回这个值
- 不是叶节点再加上左右节点的递归返回值
var sumNumbers = function(root) {
return dfs(root,0);
};
var dfs = function(p,sum) {
if(!p) return 0;
sum=sum*10+p.val;
if(!p.left&&!p.right) return sum;
return dfs(p.left,sum)+dfs(p.right,sum);
};