hdu--2586--lca_tarjan

开篇 敬仰下 大师-tarjan 发明的这些算法太流弊了=-=使用这个lca_tarjan之前 可以先去学习下使用tarjan解决scc强连通问题

我本来是去做到hdu-4912-发现做不来=-= 去网上搜了下 都说是神马lca的....那就去学下吧 而且很多也将这题当做入门题..

lca分离线和在线 这边我介绍的是离线算法 是要先将所有的询问一起处理 而不是单个单个地去处理  处理完成之后 你自己选择一种方式将答案存储下来

然后再进行一遍输出答案

我再网上没有找到一篇好的博客来推荐给大家 所以这边我就不写 传送门的故事了 -.-

学习下它 对于你的思想 是很有帮助的 很多时候 都是这样

这边我们需要用到 并查集来优化这个算法

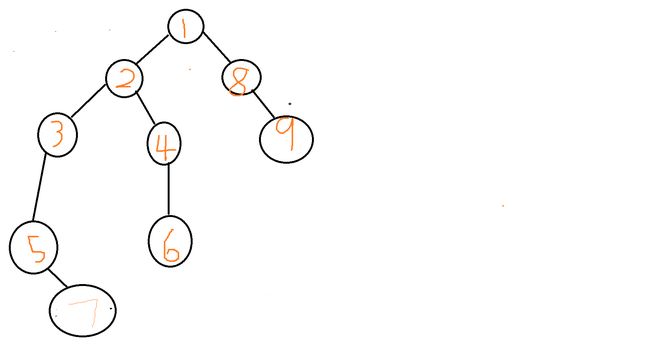
我们结合下图 进行分析

 

现在 我们以上图为例 建立的边<无向>

1<-->2   2<-->3   2<--->4   3<--->5   5<--->7   2<--->4  4<--->6  1<--->8  8<--->9

我们的询问就是

lca:<2,3>  ,   <5,6>    ,    <7,4>      ,    <9,3>

这4组查询结果也算都是有一些特点的吧  虽然我们很容易地可以从上图中得到结果

2 3肯定是2啊 因为3是2的子树下的结点

5 6就是2了 他们同时是2的子树的结点 你也当然会说他们也是1的子树的结点啊 但是2的深度更大 离根结点更远

还有2个就先不说了.....

既然 这是树 那我们解决的时候首先就自己确定一个根结点 按习惯上 我们都喜欢默认1当做根结点 当然你也可以2 3 ……n

草。。我突然发现 不会分析下去了..

就是要注意下 假设你当前访问到的结点是u 现在有一个结点是v与u相邻 那么假如v没有被访问过 那就再lca_tarjan(v)即去访问v 这边的后续操作要明白 既然u与v相邻 那我们可以将他们看成是在同一棵子树上的 所以我们将v所在的集合并在u所在的集合之下 这时 就需要用到并查集了 

 

很多人会习x = find(u)  y = find(v) father[y] = x;

但其实 我觉得 直接father[v] = u就足够了 因为你find的结果肯定是自身结点 如若不是 那就是成环了 这样本来就不可以使用tarjan去解决了

//我也不确定上面我的理解是否正确 如若错误 一定要告诉我啊...

当然 在我们接下去询问求u v的lca的时候 是一定要用 find(v)的 因为v是比u先遍历到的 离根结点更近 因为可能会出现如 上图询问《5,6>这样的情况 这时候 father[5]=3 这是没有错的 但<5,6>的lca就是2了 所以我们这边必须是要find(v)的 就是用来针对这种情况 假如这棵子树的根结点是A 假设只有B C与它相连 而我们是询问B C这2棵子树下的lca 而我们递归回溯过来更新father[]是更新到直接与它相邻的为止 so 需要进行find操作 在2棵不同的子树情况下

这边最好去理解下 子树的概念 这在数据结构有涉及到 这个可以是递归定义的

可能有些 言不达意 =-= 都是自我理解 大家可以多参考一些博客 然后自己模拟画画 就是了

 

  1 #include 
  2 #include 
  3 using namespace std;
  4 
  5 int cnt1 , cnt2;
  6 const int size1 = 40010;
  7 const int size2 = 210;
  8 struct graph
  9 {
 10     int from;
 11     int to;
 12     int val;
 13     int next;
 14     int lca;
 15 };
 16 graph edge[size1*2];
 17 int Ehead[size1];
 18 graph node[size2*2];
 19 int Nhead[size1];
 20 bool vis[size1];
 21 int dist[size1];
 22 int father[size1];
 23 
 24 void init( )
 25 {
 26     memset( Ehead , -1 , sizeof(Ehead) );
 27     memset( Nhead , -1 , sizeof(Nhead) );
 28     memset( dist , 0 , sizeof(dist) );
 29     memset( vis , false , sizeof(vis) );
 30 }
 31 
 32 int find( int x )
 33 {
 34     return x == father[x] ? x : father[x] = find( father[x] );
 35 }
 36 
 37 
 38 void addEdge( int from , int to , int val )
 39 {
 40     edge[cnt1].to = to;
 41     edge[cnt1].val = val;
 42     edge[cnt1].next = Ehead[from];
 43     Ehead[from] = cnt1 ++;
 44 }
 45 
 46 void addQueryEdge( int from , int to )
 47 {
 48     node[cnt2].from = from;
 49     node[cnt2].to = to;
 50     node[cnt2].next = Nhead[from];
 51     Nhead[from] = cnt2 ++;
 52 }
 53 
 54 void lca_tarjan( int u , int val )
 55 {
 56     int v , x , y;
 57     vis[u] = true;
 58     dist[u] = val;
 59     father[u] = u;
 60     for( int i = Ehead[u] ; ~i ; i = edge[i].next )
 61     {
 62         v = edge[i].to;
 63         if( !vis[v] )
 64         {
 65             lca_tarjan( v , edge[i].val + val );
 66             x = find(u);
 67             y = find(v);
 68             if( x!=y )
 69             {
 70                 father[y] = x;
 71             }
 72         }
 73     }
 74     for( int i = Nhead[u] ; ~i ; i = node[i].next )
 75     {
 76         v = node[i].to; 
 77         if( vis[v] )
 78         {
 79             node[i].lca = node[i^1].lca = find(v);
 80         }
 81     }
 82 }
 83 
 84 int main()
 85 {
 86     cin.sync_with_stdio(false);
 87     int t , from , to , val , ans , id;
 88     int n , m;
 89     cin >> t;
 90     while( t-- )
 91     {
 92         init( );
 93         cin >> n >> m;
 94         cnt1 = cnt2 = 0;
 95         for( int i = 1 ; i )
 96         {
 97             cin >> from >> to >> val;
 98             addEdge( from , to , val );
 99             addEdge( to , from , val );
100         }
101         for( int i = 0 ; i )
102         {
103             cin >> from >> to;
104             addQueryEdge( from , to );
105             addQueryEdge( to , from );
106         }
107         lca_tarjan( 1 , 0 );
108         for( int i = 0 ; i )
109         {
110             id = i * 2;
111             ans = dist[ node[id].from ] + dist[ node[id].to ] - 2*dist[ node[id].lca ];
112             cout << ans << endl;
113         }
114     }
115     return 0;
116 }

View Code

忘了一个很重要的...lca是基于 无向无环图的 也可以说多叉树吧 我是觉得差不多的

 

today:

　　我们最大的敌人就是自己

　　我们的恐惧来源于对自己的否定

　　信心才是最重要的

 

转载于:https://www.cnblogs.com/radical/p/3945072.html