最近想学习Libra数字货币的MOVE语言,发现它是用Rust编写的,所以先补一下Rust的基础知识。学习了一段时间,发现Rust的学习曲线非常陡峭,不过仍有快速入门的办法。
学习任何一项技能最怕没有反馈,尤其是学英语、学编程的时候,一定要“用”,学习编程时有一个非常有用的网站,它就是“欧拉计划”,网址: https://projecteuler.net
英文如果不过关,可以到中文翻译的网站:
http://pe-cn.github.io/
这个网站提供了几百道由易到难的数学问题,你可以用任何办法去解决它,当然主要还得靠编程,编程语言不限,论坛里已经有Java、C#、Python、Lisp、Haskell等各种解法,当然如果你直接用google搜索答案就没任何乐趣了。
学习Rust最好先把基本的语法和特性看过一遍,然后就可以动手解题了,解题的过程就是学习、试错、再学习、掌握和巩固的过程,学习进度会大大加快。
- 第1~6题
- 第7~12题
- 第13~16题
- 第17~21题
第26题
问题描述:
单位分数指分子为1的分数。
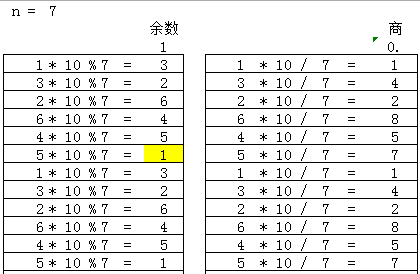
1/6= 0.1(6) 表示0.166666…,括号内表示有一位循环节。
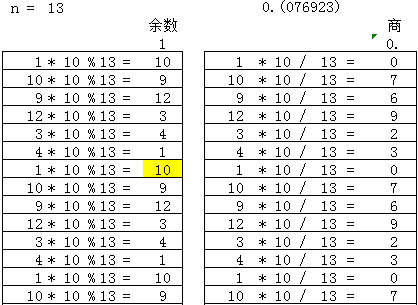
1/7= 0.(142857),1/7有六位循环节。
找出正整数d < 1000,其倒数的十进制表示小数部分有最长的循环节。
通过手算找到规律,
再找一个分母大于10的:
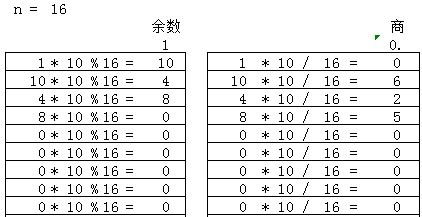
再找一个能除尽的:
可以发现几个特点:
1)分子为1,表示一开始的余数为1
2)余数为0时,表示可以除尽,循环要终止
3)当余数重复出现时,表示找到了循环节,2个重复出现的位置就是循环节
按照这个逻辑,循环节的长度可以求出,这里用两个向量分别存储余数remainders和商digits。
fn reciprocal_cycle(d: u32) -> u32 {
let mut remainders : Vec = vec![1]; //余数
let mut digits : Vec = vec![]; //商
let mut numerator = 1; //分子
while numerator != 0 {
digits.push(numerator * 10 / d);
numerator = numerator * 10 % d; //余数
let pos = remainders.iter().position(|&x| x==numerator);
match pos {
Some(x) => { //余数重复出现时
return (digits.len() - x) as u32;
}
None => {
remainders.push(numerator);
}
}
}
0 //除尽的时候,表示循环节为0
} 这里在向量里查找一个元素的位置索引时用了position函数,返回是一个Option类型,用match语句针对不同的情况进行处理。
主程序就简单了:
let mut max_cycle: u32 = 0;
for n in 2..1000 {
let rc = reciprocal_cycle(n);
if rc > max_cycle {
println!("n={} cycle={}", n, rc);
max_cycle = rc;
}
}
println!("max reciprocal cycle: {}", max_cycle);优化:实际上商并不需要存储,可以减少一个向量,求循环节的函数还可以精简一下。
fn reciprocal_cycle(d: u32) -> u32 {
let mut remainders : Vec = vec![1]; //余数
let mut numerator = 1; //分子
while { numerator = numerator * 10 % d; numerator != 0} {
let pos = remainders.iter().position(|&x| x==numerator);
match pos {
Some(x) => { //余数重复出现时
return (remainders.len() - x) as u32;
}
None => {
remainders.push(numerator);
}
}
}
0 //除尽的时候,表示循环节为0
}