三.treap树
Treap树是把BST和Heap结合起来了,即具有BST的性质又利用堆维持树的平衡。因此树的节点需要储存一个优先级项(优先级具有随机性,在节点创立时生成)来维持堆的属性。
Treap树同样有查找、插入和删除操作。它插入和删除的期望时间为O(logN),但查找的时间却同查找非平衡二叉树一样慢。
图3-1 treap树的示意图
相对,treap树的插入和删除代码则相对简单一些,如下,
四.后缀数组
在进行模式匹配,如找出为本T中是否存在子串与P匹配、模式P在T中出现的次数或者是模式P都在文本T中的哪些地方出现。而这些问题都可以利用后缀数组很好的进行解决。
后缀数组就是文本T依次排列的所有后缀的数组,而LCP是后缀数组中,每对相邻子串的最长公共前缀,可以加速模式匹配问题的处理速度,
| 顺序 |
下标 |
LCP |
所表示的子串 |
| 0 |
5 |
- |
a |
| 1 |
3 |
1 |
ana |
| 2 |
1 |
3 |
anana |
| 3 |
0 |
0 |
banana |
| 4 |
4 |
0 |
na |
表4-1 “banana”的后缀数和LCP
关于文本T的后缀数组的构建有一种线性时间的构建方法,构建步骤如下。
第一步:将源字符串的字符排序,从1开始顺序地给这些字符分配数字;
第二步:把文本分成3组:
比如,文本ABRACADABRA的三元字符组为
第三步:把S1和S2连接起来并递归地计算后缀数组。
如,文本ABRACADABRA的S1和S2得到的后缀数组,如下
| S1S2 |
[BAR] |
[CAD] |
[ABR] |
[A$$] |
[RAC] |
[ADA] |
[BRA] |
| 整数 |
4 |
5 |
2 |
1 |
6 |
3 |
4 |
| SA[S1S2] |
3 |
2 |
5 |
6 |
0 |
1 |
4 |
| 下标 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
第四步:计算S0的后缀数组,S1中建立的排名可以直接用在S0的第一趟基数排序上,第二趟是对S0中的单个字符排序,字符相匹配的利用第一趟的排序处理。
如,文本ABRACADABRA的S0的后缀计算,
|
|
S0 |
|||
|
|
[ABR] |
[ACA] |
[DAB] |
[RA$] |
| 文本中下标 |
0 |
3 |
6 |
9 |
| 第2个元素的下标 |
1 |
4 |
7 |
10 |
| 第一趟基数排序 |
5 |
6 |
2 |
1 |
| 第二趟基数排序 |
1 |
2 |
3 |
4 |
| 组中名次 |
1 |
2 |
3 |
4 |
| 使用文本中下标表示的SA |
0 |
3 |
6 |
9 |
第五步:使用合并两个排序的表的标准算法合并S0和S1S2的后缀数组,
|
|
A |
A |
D |
R |
| S0的后缀数组 |
0 |
3 |
6 |
9 |
|
|
A |
A |
A |
B |
B |
C |
R |
| S1S2的后缀数组 |
10 |
7 |
5 |
8 |
1 |
4 |
2 |
| 最终文本的后缀数组 |
10 |
7 |
0 |
3 |
5 |
8 |
1 |
4 |
6 |
9 |
2 |
| 文本 |
A |
B |
R |
A |
C |
A |
D |
A |
B |
R |
A |
| 下标 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
五.k-d树
k-d树是对数据点在k维空间中进行划分的一种数据结构,主要应用于多维空间关键数据的搜索(如:范围搜索和最邻近搜索)。k-d树实质上也是一种二叉树。
2-d树,即二维查找树,其具有以下性质:在奇数层上按照第一个关键字进行分支,在偶数层上则按照第二个关键字进行。
2-d树和随机二叉查找树一样,平均高度为O(logN),但最坏情形是O(N)。然而,2-d树不存在类似旋转的操作使其高度维持在O(logN)水平上。因此,2-d树的查找和插入等操作的平均时间复杂度为O(logN),最坏情形为O(N)。
范围查找是k-d树的一项应用,即找出第k个关键字符合给定范围的所有项。2-d树的范围查找也即找出第一个关键字符合给定范围且第二个关键字也在给定范围内的所有的项,2-d树的范围查找例程如下,
图5-1 2-d树的范围查找
六.配对堆
配对堆被表示成堆序树,即用左儿子,右兄弟的表示方法。配对堆的性能分析未解决,但decreaseKey操作胜过其他对结构,同样对于配对堆,其插入和删除的基本操作都是基于合并。
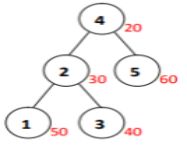
图6-1 配对堆的抽象表示法(左)和树形表示法(右)
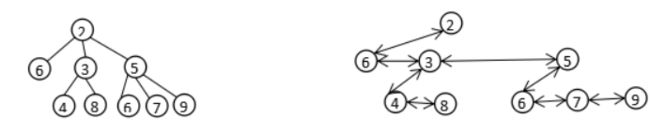
下图为两个子堆的合并过程示意图,其中第二个子堆可以有兄弟的情况,合并即让较大根的子堆成为另一个子堆的最左的儿子。
图6-2 两个子堆合并示意图
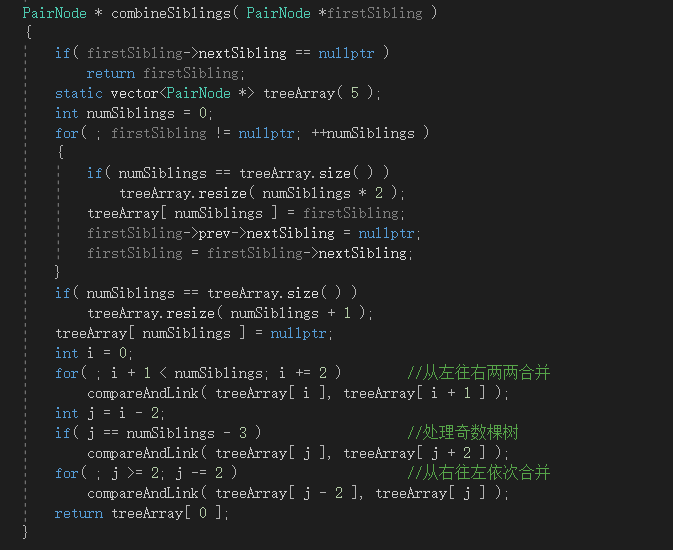
由配对堆的合并过程较简单,其代码的实现如下,
图6-3 配对堆的合并代码
配对堆的删除操作则相对复杂些,在DeleteMin后,会留下根的一堆子堆,需要将这些子堆最终合并为一个堆。而合并这些子堆所利用的方法为两趟合并法。
第一趟从左往右,两个堆两个堆地合并。第二趟则从右往左,依此往右合并,直至最终合并成一个堆。
图6-4 配对堆删除操作后的合并子堆代码