作者 | 文永亮
学校 | 哈尔滨工业大学(深圳)
研究方向 | 目标检测、GAN
推荐理由
这是一篇发表于CVPR2019的paper,是浙江大学和香港中文大学的工作,这篇文章十分有趣,网友戏称:“无痛涨点,实现简单,良心paper。”,在我看来确实是这样的,没有太大的改造结构,不需增加计算成本的条件下,居然能涨两个点mAP。除了本文解读的Libra R-CNN(天秤座 RCNN)[1],我还记得陈恺他们港中文的实验室今年还中了一篇CVPR2019是《Region Proposal by Guided Anchoring》[2],这篇也是不错的,看题目就知道是指导anchor的形状涨分的了。
这两篇改进的源码都会在github上放出,作者表示还在完善中,地址是:https://github.com/open-mmlab/mmdetection
三个不平衡
纵观目前主流的目标检测算法,无论SSD、Faster R-CNN、Retinanet这些的detector的设计其实都是三个步骤:
- 选择候选区域
- 提取特征
- 在muti-task loss下收敛
往往存在着三种层次的不平衡:
- sample level
- feature level
- objective level
这就对应了三个问题:
- 采样的候选区域是否具有代表性?
- 提取出的不同level的特征是怎么才能真正地充分利用?
- 目前设计的损失函数能不能引导目标检测器更好地收敛?
其实如果不对detector的结构做功夫的话,针对这些imbalance改进的其实就是为了把detector的真正功效给展现出来,就是如果把一个目标检测器train好的问题。
对应的三个改进
IoU-balanced Sampling
作者认为sample level的不平衡是因为随机采样造成的,Ross Girshick后面提出了OHEM(online hard example mining,在线困难样本挖掘)是一个hard negative mning的一种好方法,但是这种方法对噪音数据会比较敏感。随机采样造成的不平衡可以看下图:
作者发现了如果是随机采样的话,随机采样到的样本超过70%都是在IoU在0到0.05之间的,有人会问不是随机吗?为什么大部分样本都落在了IOU较小的部分了呢?因为样本的分布在IoU上并不是均匀分布的,生成候选框时随机采样会造成背景框远远大于框中GT的框,一张图这么大,是目标物体的区域只占很小一部分,背景占了绝大多数的位置,所以大部分样本都挤在了IoU在0到0.05的区间了,作者觉得这里就是不科学的地方,统计得到的事实是60%的hard negative都落在IoU大于0.05的地方,但是随机采样只提供了30%。所以作者提出了IoU-balanced Sampling。
随机采样就是比如你要选N个hard negative,有M个候选框,选中的概率就是:
\[ p = \frac{N}{M} \]
如果一共还是要采样N个,通过IoU的值划分为K个区间,每个区间中的候选采样数为\(M_k\),则IoU-balanced sampling的采样公式即为:
\[ p_{k}=\frac{N}{K} * \frac{1}{M_{k}}, \quad k \in[0, K) \]
作者通过在IoU上均匀采样, 把hard negative在IoU上均匀分布,在COCO数据集上达到的效果比OHEM的要好,并且这样简单很多。
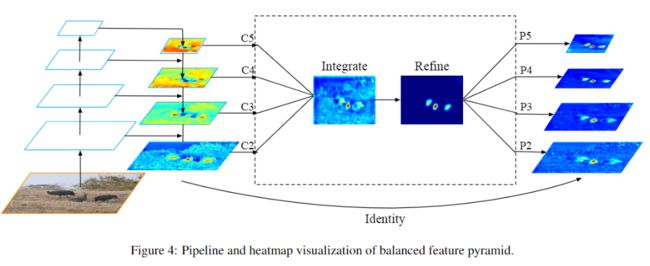
Balanced Feature Pyramid
feature level的不平衡表现在low/high level特征的利用上,如何利用不同分辨率的特征,分为了四步:rescaling,integrating,refining,strengthening。
rescaling & integrating :
假设\(C_l\)表示第\(l\)层特征,越高层分辨率越低,若有\({}{C_2, C_3, C_4, C_5}\)的多层特征,\(C_2\)分辨率最高,我们知道低层特诊分辨率高往往学习到的是细节特征,高层特征分辨率低学习到语义特征,把四层特征resize到中间层次的\(C_4\)的size,然后后面再做简单的相加取平均操作:
\[ C=\frac{1}{L} \sum_{l=l_{\min }}^{l_{\max }} C_{l} \]
就是这样简单的操作并没有引入什么计算就可以实现,最终在AP上也得到了验证是有效的。
refining & strengthening:
rescaling后取平均提取到的的特征还可以进一步地refine成更discriminative,作者这里用到了non-local模块,paper中使用了Gaussian non-local attention [4]增强integrate后的特征。
就像Figure 4画的一样,这样提取的特征其实与FPN可以一同使用,是作为feature pyramid的补充,作为一种增强手段。
Balanced L1 Loss
Fast R-CNN [5]中是通过multi-task loss解决Classification(分类)和Localization(定位)的问题的,定义如下:
\[ L_{p, u, t^{u}, v}=L_{c l s}(p, u)+\lambda[u \geq 1] L_{l o c}\left(t^{u}, v\right) \]
\(L_{cls}\) 和\(L_{loc}\) 分别对应着分类和定位的损失函数, \(p\) , \(u\) 分别是\(L_{cls}\) 的预测和目标,\(t^u\)是对应\(u\)类的回归结果。 \(v\)是回归目标。 \(\lambda\)用于在多任务学习下调整损失权重。
之所以会提出Balanced L1 loss,是因为这个损失函数是两个loss的相加,如果分类做得很好地话一样会得到很高的分数,而导致忽略了回归的重要性,一个自然的想法就是调整\(\lambda\) 的值。我们把样本损失大于等于1.0的叫做outliers,小于的叫做inliers。由于回归目标是没有边界限制的,直接增加回归损失的权重将会使模型对outliers更加敏感。对于outliers会被看作是困难样本(hard example),这些困难样本会产生巨大的梯度不利于训练得过程,而inliers被看做是简单样本(easy example)只会产生相比outliers大概0.3倍的梯度。
首先我们看Smooth L1 Loss:
\[ L1_{smooth} = \left\{\begin{array}{ll}0.5x^2 & {\text{|x|<1} (inliers)}\\|x|-0.5 & {\text{otherwise(outliers)}}\end{array}\right. \]
\[ \frac{\partial L1_{smooth}}{\partial x} = \left\{\begin{array}{lll} x & \text{|x|<1}\\ -1 & \text{x<-1} \\ 1 & \text{x>1} \end{array}\right. \]
所以作者从常见的Smooth L1 Loss中推导出了Balanced L1 Loss:
\[ L_{l o c}=\sum_{i \in\{x, y, w, h\}} L_{b}\left(t_{i}^{u}-v_{i}\right) \]
它的梯度计算遵从下面的准则:
\[ \frac{\partial L_{l o c}}{\partial w} \propto \frac{\partial L_{b}}{\partial t_{i}^{u}} \propto \frac{\partial L_{b}}{\partial x} \]
作者从需求出发,想要得到一个梯度当样本在\(|x|<1\)附近产生稍微大点的梯度,作者设计了下面这个函数,从Figure 5可以看出\(\alpha\ln (b|x|+1)\)大于x。
\[ \frac{\partial L_{b}}{\partial x}=\left\{\begin{array}{ll}{\alpha \ln (b|x|+1)} & {\text { if }|x|<1} \\ {\gamma} & {\text { otherwise }}\end{array}\right. \]
根据梯度反求出\(L_{b}(x)\) 表达式:
\[ L_{b}(x)=\left\{\begin{array}{ll}{\frac{\alpha}{b}(b|x|+1) \ln (b|x|+1)-\alpha|x|} & {\text { if }|x|<1} \\ {\gamma|x|+C} & {\text { otherwise }}\end{array}\right. \]
还有很重要的一点就是为了函数的连续性,需要满足x=1时\(L_{b}(1)=\gamma\):
\[ \alpha \ln (b+1)=\gamma \]
其实意思就是\(b=e^{\frac{\gamma}{\alpha}}\).
这个函数不得不说非常妙,成功掰弯了梯度,我也不知道他怎么想出来的。
实验结果
在COCO test-dev数据集上与目前state-of-the-art的目标检测的方法对比,能比Faster R-CNN、RetinaNet、Mask R-CNN要高2+的AP。
三种解决方案的各种组合情况的对比实验:
值得注意的是,作者对IoU-balanced samping做实验时对K的取值做了实验证明该方法对K的取值并不敏感,即对IoU分多少个区间并不敏感。
这是IoU-balanced sampling的候选框的可视化效果:
总结
paper逻辑清晰,紧紧抓住三个层次去做改进,三个问题对应三个解决方案,结构清晰一目了然,实验充分,相比两个单阶段和两阶段检测器的两个代表Faster R-CNN和RetinaNet分别高了2+的AP,图画得也不错,我觉得是篇好论文,而且应该是作者在比赛中实际运用到的才写出了这篇paper,以后目标检测的比赛我觉得都可以参考这篇去做改进。
参考文献
[1]. Pang J, Chen K, Shi J, et al. Libra R-CNN: Towards Balanced Learning for Object Detection[J]. arXiv preprint arXiv:1904.02701, 2019.
[2]. Wang J, Chen K, Yang S, et al. Region proposal by guided anchoring[J]. arXiv preprint arXiv:1901.03278, 2019.
[3]. Shrivastava A, Gupta A, Girshick R. Training region-based object detectors with online hard example mining[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 761-769.
[4]. Wang X, Girshick R, Gupta A, et al. Non-local neural networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 7794-7803.
[5]. Ross Girshick. Fast r-cnn. In IEEE Conference on Computer Vision and Pattern Recognition, 2015.