2 模型
2.1 距离测量
2.2 k值选择
2.3 分类决策规则
3 kNN的实现——kd树
3.1 构造kd树
3.2 kd树搜索
1 k近邻算法
k nearest neighbor,k-NN,是一种基本分类与回归的方法,输入为实例的特征向量——对应空间的点,输出为实例的类别,可取多类。kNN假定一个训练集,实例类别已确定,分类时,对新的实例根据其k个最近邻训练集实例的类别,通过多数表决的方式进行预测。不具有显式学习过程。利用训练集对特征空间划分,并作为其分类的model。三要素是k值的选择,距离度量,分类决策规则。1968年Cover和Hart提出。
算法:

I为指示函数,即当yi=cj时I=1,否则I=0
2 模型
kNN的model对应于特征空间的划分,有三个要素:k选择,距离度量,分类决策。对于每个实例x,当三要素确定后,就能得到其所在的对特征空间的划分单元cell。
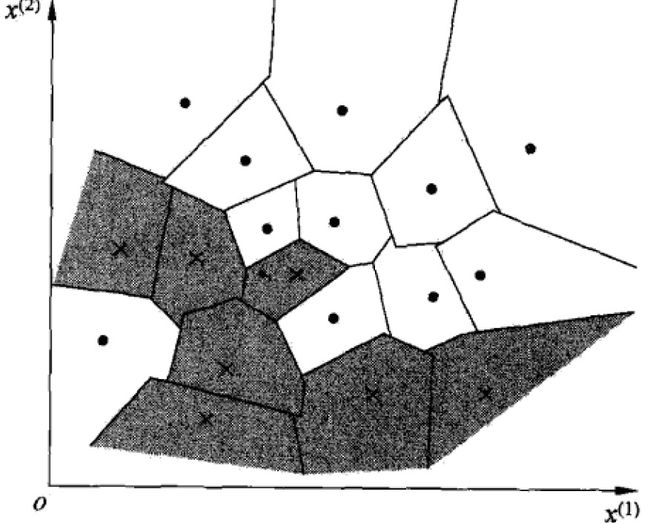
2.1 距离测量
特征空间中,两个实例点的距离其实是相似度的反应,距离越近越相似。一般对于特征空间Rn,常用欧氏距离(Euclidean distance),也可以更一般的Lp距离或Minkowski距离。
几种距离度量方法:



2.2 k值选择
k选择较小的时候,对实例较小的邻域进行预测,近似误差(approximation error)会减小,只有与输入实例较近的训练实例才会起作用。缺点是估计误差(estimation error)会增大,预测结果对近邻的实例点会非常敏感。总之,k值减小,意味着模型复杂度增大,容易发生过拟合。
同样的,较大k值意味着较大邻域训练,近似误差增大,估计误差减少,离实例点较远的点也会对预测起作用,使预测发生错误,意味着模型过于简单。
在实际应用中,常取较小的k值,采用交叉验证来选取最优 k值。
2.3 分类决策规则
kNN采用多数表决规则(majority voting rule):由输入实例的k个近邻的训练实例中,多数类决定输入实例的类别。
多数表决规则数学含义是经验风险最小化:
证明:
若loss function是0-1损失函数,分类函数为:f:Rn——>{c1,c2,…,ck}
误分类率是:P(Y!=f(X)) = 1-P(Y=f(X))

可以看到误分类率最小就是经验风险最小,就要 使得右边Sigma(I(yi=cj))最大,即多数表决!
3 kNN的实现——kd树
KNN最简单的实现是线性扫描(linear scan),要求计算输入实例与训练实例的每一个距离,当训练集很大时,这样扫描十分耗时,因此考虑到如何对特征空间和维数大,容量大的训练数据进行快速的搜索,十分必要。可以考虑特殊的存储结构训练数据,以减少计算距离的次数,比如kd树(kd tree)方法。
3.1 构造kd树
kd树是一种对k维空间实例点进行存储以便于快速检索的数据结构。kd树是二叉树,表示对k维空间的一个划分(partition)。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间划分,构成一系列k维超矩形区域,kd树的每个节点对应于一个k维超矩形区域。
构造方法:首先构造根节点——对应于k维空间中包含所有实例点的超矩形区域;通过递归方法,不断对k维空间进行划分生成子节点,在此超矩形区域上选择一个坐标轴和一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子节点),这时实例被分到两个子区域,这个过程持续到区域内没有实例时终止,终止时节点为叶子结点。在此过程中将实例保存在相应的结点上。
通常,依次选择坐标轴对空间切分,选择训练实例点在选定坐标轴的中位数(median)为切分点,得到平衡kd树——但是不一定是搜索效率最优。
平衡kd树算法:


针对高维数据需要对每一维都进行二分,更好的方法是对方差最大的特征进行比较和划分。(具体可看文末的博文推荐)
3.2 kd树搜索
利用kd树进行k近邻搜索
给定一个目标点,搜索其最近邻。首先找到包含该目标点的叶子结点,然后从叶子结点出发,一次回退到父结点;不断查找与目标结点最近邻的结点,当确定不可能存在更近的结点时终止。这样搜索就会限制在空间的局部区域上,效率大为提高。
包含目标结点的叶子结点对应包含目标点的最小超矩形区域,以此叶子结点的实例点当做当前最近点,目标点最近邻一定在以目标点为中心并通过当前最近点的超球体内部。然后返回当前结点的父节点,如果父节点的另一子节点超矩形区域与超球相交,那么就在相交区域寻找与目标点的更近实例点,若存在,就当做当前最近点,算法转到更上一级的父节点,继续迭代上述过程,父节点的另一子节点超矩形区域与超球体不想交,或不存在当前最近点更近的点,则停止搜索。
kd树最近邻搜索算法:


算法复杂度为O(logN),而不是之前的O(N),更适合实例数目远远大于空间维数的情况,当二者接近时效率将降低为线性扫描
推荐读一读这篇博文,比书上写的更通俗一些。
K-D Tree原理及实现