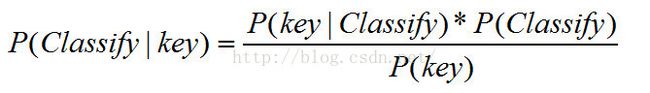前言:
如果你想对一个陌生的文本进行分类处理,例如新闻、游戏或是编程相关类别。那么贝叶斯分类算法应该正是你所要找的了。贝叶斯分类算法是统计学中的一种分类方法,它利用概率论中的贝叶斯公式进行扩展。所以,这里建议那些没有概率功底或是对概率论已经忘记差不多的读者可以先去学习或是温习一下《概率论与数理统计》中的条件概率那一个章节。
由于贝叶斯定理假设一个属性值对给定类的影响独立于其它属性的值,而此假设在实际情况中经常是不成立的,因此其分类准确率可能会下降。为此,就衍生出许多降低独立性假设的贝叶斯分类算法,如TAN(tree augmented Bayes network)算法。关于TAN算法不在本文的叙述范围之内,这里我们不作讨论。
下面我们就针对朴素贝叶斯分类算法,进行原理浅析和文本分类实践(这里笔者使用Java语言开发)。
本文链接:http://blog.csdn.net/lemon_tree12138/article/details/48520315 --Coding-Naga
--转载请注明出处
公式说明:
1.全概率公式:
2.贝叶斯公式:
上面的两个公式是最简单的两个公式说明,旨在简化理解。
思路分析:
在开始理解贝叶斯算法之前,独立于本文之外。如果有人问你如何让程序给一篇陌生的文章分类?你要怎么做呢?
我能想到的就是以关键词来区分。比如分类为邮箱的类别中,我选取三个关键词:邮箱、邮件和收发。然后使用这三个关键词在文章中去依次查找,统计出此三个关键词总共出现了多少次,再与其他的类别进行比较。次数最多的即为这篇文章的分类。如果要再精确一些,可以采用不同权重的方式,上面说的方法,权重为1。如果采用权重的策略,那么这里就不是出现次数最多的类别了,而是以计分的方式,次数*权重并累加。最高分的类别即为本文的分类。
当然,这是一种解决方法。这个其实跟贝叶斯分类算法还是有一些类似的,有了这种想法,再去理解贝叶斯就容易得多了。
流程说明:
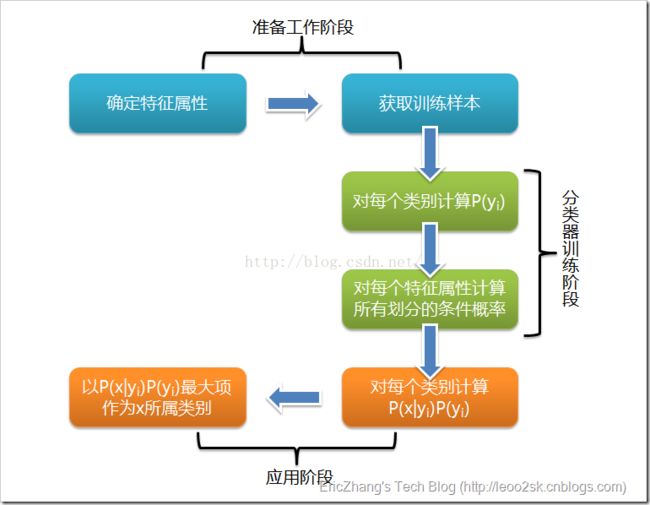
朴素贝叶斯分类的流程可以由下图表示(图片来源网络):
针对上图有一些需要说明的地方,首先这张流程图的确可以很清楚地表达我们朴素贝叶斯模型的流程。需要注意的是,这里如果P(x|yi)中的x如果是在训练集中不存在的一个特征值,我们是无法进行计算它的先验概率的。不过还好,因为x在训练中不存在,那么我们就可以粗略认为,x是一个与yi无关的值,即概率为0。
代码展示:
1.准备阶段:
在准备阶段有两个步骤,确定特征属性和获取样本。确定特征属性这个会因个人对分类的理解以及需求不同而不同;而获取样本则是比较简单的读取文件。如下:
/**
* 读取训练文档中的训练数据
* 并进行封装
*
* @param filePath
* 训练文档的路径
* @return
* 训练数据集
*/
public static ArrayList> read(String filePath) {
if (Tools.isEmptyString(filePath)) {
return null;
}
ArrayList> trainningSet = new ArrayList>();
List datas = readFile(filePath);
ArrayList singleTrainning = null;
for (int i = 0; i < datas.size(); i++) {
String[] characteristicValues = datas.get(i).split(" ");
singleTrainning = new ArrayList();
for (int j = 0; j < characteristicValues.length; j++) {
if (!Tools.isEmptyString(characteristicValues[j])) {
singleTrainning.add(characteristicValues[j]);
}
}
trainningSet.add(singleTrainning);
}
return trainningSet;
} 2.训练阶段:
在训练阶段,我们就是预先计算出一些先验概率,这些先验概率是与待计算的特征值x无关的。不关这个x是否在训练集中存在,都是无关的,这个在前面已经说过了。那么先验概率主要有P(classify),P(key)和P(key|classify)。
P(classify):
/**
* 预先计算出每个分类出现的概率
*
* @param map
* 所有分类总的数据集
* @param classifyProbablityMap
* 每个分类classify的出现概率
*/
public void preCalculateClassifyProbablity(Map>> map, Map classifyProbablityMap) {
if (map == null || classifyProbablityMap == null) {
return;
}
Object[] classes = map.keySet().toArray();
int totleClassifyCount = 0;
for (int i = 0; i < classes.length; i++) {
totleClassifyCount += map.get(classes[i].toString()).size();
}
if (totleClassifyCount == 0) {
return;
}
for (int i = 0; i < classes.length; i++) {
if (!classifyProbablityMap.containsKey(classes[i])) {
classifyProbablityMap.put(classes[i].toString(), 1.0 * map.get(classes[i]).size() / totleClassifyCount);
}
}
}
/**
* 预先计算出每个关键字出现的概率
* TODO
* @param map
* 所有分类总的数据集
* @param keyProbablityMap
* 每个特征值key的出现概率
*/
public void preCalculateKeyProbablity(Map>> map, Map keyProbablityMap) {
if (map == null || keyProbablityMap == null) {
return;
}
Object[] classes = map.keySet().toArray();
String key = "";
int totleKeyCount = 0;
for (int i = 0; i < map.size(); i++) {
ArrayList> classify = map.get(classes[i]);
ArrayList featureVector = null; // 分类中的某一特征向量
for (int j = 0; j < classify.size(); j++) {
featureVector = classify.get(j);
for (int k = 0; k < featureVector.size(); k++) {
key = featureVector.get(k);
totleKeyCount++;
if (keyProbablityMap.get(key) == null) {
keyProbablityMap.put(key, 1.0);
} else {
keyProbablityMap.replace(key, keyProbablityMap.get(key) + 1.0);
}
}
}
}
if (totleKeyCount == 0) {
return;
}
Set keys = keyProbablityMap.keySet();
for (String string : keys) {
keyProbablityMap.replace(string, keyProbablityMap.get(string) / totleKeyCount);
}
}
/**
* 计算先验概率P(key|classify)
*
* @param map
* 所有分类总的数据集
* @param keyClassifyMap
* 先验概率P(key|classify)的所有数据集
*/
public void preCalculateKeyInClassifyProbablity(Map>> map, Map> keyClassifyMap) {
if (map == null || keyClassifyMap == null) {
return;
}
// 统计每种分类共有多少个特征值
Map keyCountMap = new HashMap();
// 统计key|classify的个数
Object[] classes = map.keySet().toArray();
Map vector = null;
for (int i = 0; i < map.size(); i++) {
ArrayList> classify = map.get(classes[i]);
for (int j = 0; j < classify.size(); j++) {
ArrayList featureVector = classify.get(j);
for (int k = 0; k < featureVector.size(); k++) {
// 统计特征值
if (keyClassifyMap.containsKey(classes[i])) {
if (keyClassifyMap.get(classes[i]).containsKey(featureVector.get(k))) {
double lastValue = keyClassifyMap.get(classes[i]).get(featureVector.get(k));
vector = keyClassifyMap.get(classes[i]);
vector.put(featureVector.get(k), 1.0 + lastValue);
keyClassifyMap.replace(classes[i].toString(), vector);
} else {
vector = keyClassifyMap.get(classes[i]);
vector.put(featureVector.get(k), 1.0);
keyClassifyMap.put(classes[i].toString(), vector);
}
} else {
vector = new HashMap();
vector.put(featureVector.get(k), 1.0);
keyClassifyMap.put(classes[i].toString(), vector);
}
// 统计每种分类共有多少个特征值 keyCountMap
if (keyCountMap.containsKey(classes[i])) {
keyCountMap.put(classes[i].toString(), 1.0 + keyCountMap.get(classes[i]));
} else {
keyCountMap.put(classes[i].toString(), 1.0);
}
}
}
}
// 遍历keyClassifyMap计算概率
Map keyVector = null;
Object[] keys = null;
for (int i = 0; i < keyClassifyMap.size(); i++) {
keyVector = keyClassifyMap.get(classes[i]);
keys = keyVector.keySet().toArray();
for (int j = 0; j < keyVector.size(); j++) {
keyVector.put(keys[j].toString(), keyVector.get(keys[j]) / keyCountMap.get(classes[i]));
}
keyClassifyMap.put(classes[i].toString(), keyVector);
}
} 3.应用阶段:
对于贝叶斯的应用,即是针对上面的贝叶斯公式进行的。即计算P(classify|key)=?.
也就是说,在特征值为key时,分类为classify的概率为多少?这是我们所求的。这一步很简单,只要我们拿到公式右边的三个概率值,就可以计算出贝叶斯公式左边的值:
/**
* 计算在出现key的情况下,是分类classify的概率 [ P(Classify | key) ]
*
* @param map
* 所有分类的数据集
* @param classify
* 某一特定分类
* @param key
* 某一特定特征
* @return
* P(Classify | key)
*/
private double calProbabilityClassificationInKey(Map>> map, Map classPMap, Map keyPMap, Map> keyClassifyMap, String classify, String key) {
double pkc = (keyClassifyMap.get(classify).containsKey(key) ? keyClassifyMap.get(classify).get(key) : 0); // p(key|classify)
double pc = classPMap.get(classify); // p(classify)
double pk = keyPMap.get(key) == null ? 0 : keyPMap.get(key); // p(key)
double pck = 0.0; // p(classify | key)
if (pk == 0) {
pck = 0;
} else {
pck = (pkc * pc / pk) * pk;
}
return pck;
} 参考:
1.《概率论与数理统计》(第四版) 浙大版
2.《数据之美》
3.http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
4.http://www.ruanyifeng.com/blog/2013/12/naive_bayes_classifier.html
附件源码:
下面的代码是最初的一个版本,大家可以结合本文对代码进行修改。
http://download.csdn.net/detail/u013761665/9114225