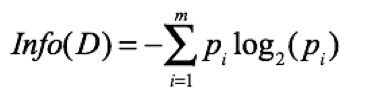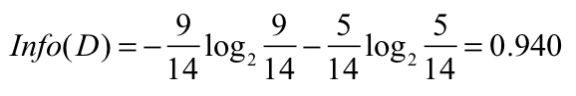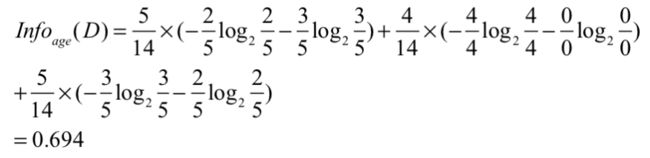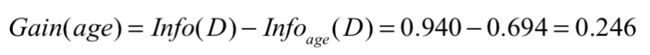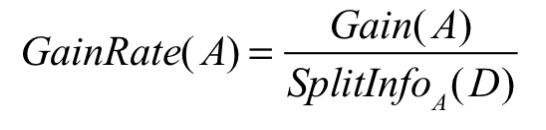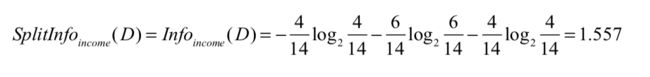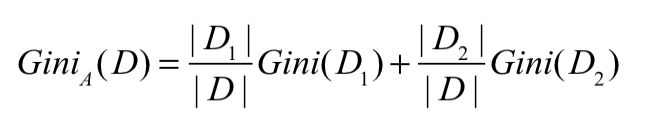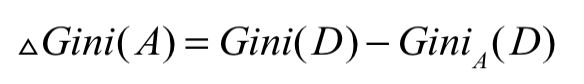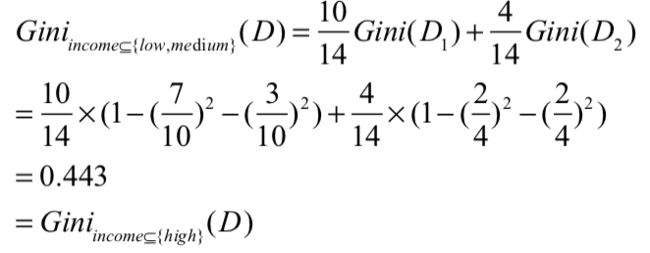一.决策树归纳
发展历程:
ID3-->C4.5-->CART
二.常用度量方法
常见的度量方法有:信息增益,增益率,基尼指数(Gini指数)
例子:
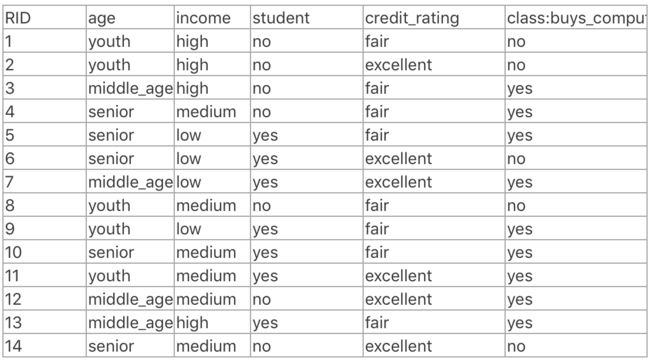
判断一个用户是否会购买电脑的数据,下面的计算都是以这里例子的数据作为计算。
属性为:age,income,student,credit_rating
label为:buys_computers(no,yes)
- 信息增益
信息熵公式定义:
其中m为分类个数,Pi为第i个类别的所有样本数量占所有样本的数量比例。这个公式衡量的是带分类样本即整个数据集D的熵。
首先,计算整个数据集的信息熵(数据集的杂乱程度)
之所以以2为底,计算机是二进制01编码的。所以显示需要0.940位才能表示整个数据集。同时说明数据集的杂乱程度为0.940.
当我们在建树的时候,应该在下一步选择哪个属性?选择这个属性之后能使整个数据集的杂乱程度减少多少?假设我们选择age作为下一步划分的属性,则age作为划分之后,数据集的杂乱程度是:
age属性下面有三个类别:youth,middle_aged,senior。分布占数据集的5/14,4/14,5/14。括号每个类别信息熵,如youth中no占比2/5,yes占比3/5。
那么以age属性划分的信息增益为:
就是说当我们以age作为划分之后,能消除数据集的杂乱程度的量为:0.246。同理其他的属性信息增益为:Gain(income)=0.029。Gain(student)=0.151,Gain(credit_rating)=0.048。我们当然是寻找消除能力最大的属性作为划分,这里就是age。就是这么不断地根据属性划分,知道达到一定条件:树高度,信息增益足够小或者不可分割了等(这部分不细说)。
对于连续值,先递增排序,然后可以根据每对相邻的值的中点划分,计算信息增益来选择。
划分属性选择: 选择新增增益最大的属性作为划分
信息增益划分的缺点:
偏向具有能分割更分散的数据的属性,例如如果划分的属性为product_id,那么最终计算出来的信息熵为0,信息增益最大。但是这种划分是没有意义的。
- 增益率
为了克服信息增益的缺点,采用增益率来作为衡量指标。
思考:既然信息增益有偏向大量值的倾向,那么找到一种方法归一化这种大量值属性的信息增益,使所有的信息增益都处在一个公平的度量环境下就好。
信息增益率的定义:
其中:
以income属性为例:
Gain(income)=0.029,而
那么信息增益率为:Gain(income)/info(income)=0.029/1.557=0.019
划分属性选择:选择最大信息增益率的属性做划分。
信息增益率的缺点:
信息增益率虽然解决了信息增益的缺点,但是它倾向于产生不平衡的划分,其中一个分区比其他分区小得多。
- 基尼指数
基尼指数要求树是二叉树,衡量的是数据集D的不纯度,基尼指数的定义为:
Pi是D中元组属于Ci类的概率。为何这里用元组了,以income为例,income下面的类型有:{low,medium,high} 三个类别。这三个类别产生的元组为:{low,medium,high},{low,medium},{low,high},{medium,high},{low},{medium},{high}和{}。这些都是income属性下面的类别产生的划分元组,不考虑全集{low,medium,high}和空集,那么如果一个属性下面有v个类别,则有2^2-1种划分方式。
拿属性A中的其中一个元组作为划分,将数据集D划分为D1,D2两个部分。则D的阻尼指数为:
那么根据这个元组的划分导致的不纯度降低为:
例子:
根据一开始的数据,先计算整个数据集的基尼指数,9个样本属于buys_computer=yes,5个属于buys_computer=no。根节点的基尼指数为:
根据income这个属性来划分,考虑其中一个元组{low,medium}的划分,属于{low,medium}的划分到D1,其余的划分到D2。该划分产生的基尼指数为:
以此类推,可以计算其他元组的基尼指数,然后计算不纯度降低了多少,选择不纯度降低最大的作为分裂的准则,产生两个分支,然后再往下走。
由于基尼指数的要求的是二元划分,所以计算量大很多。特别是在连续值的时候。
划分属性选择: 选择基尼指数最小的属性作为划分
基尼指数的缺点:
偏向多值属性,当类的数量大时候计算很困难。
三.总结
1.根据信息增益最大的属性作为分裂节点
2.根据信息增益率最大的属性作为分裂节点
3.根据阻尼指数最小的属性作为分裂节点
其他属性度量方法(还没去研究):卡方检验,C-SEP,G-统计量
参考:
书籍《数据挖掘概念与技术》第8章第214页。