数据结构大总结系列之B树
一,B-树
B树是为磁盘或其他直接存储辅助存储设备而设计的一种平衡二叉查找树(通常说的B树是B-树,在1972年由R.Bayer和E.M.McCreight提出,B+树是B树的一种变形),B树与红黑树类似,但在降低磁盘I/O操作次数方面要更好一些,数据库就是通常用B树来进行存储信息。
B树的结点可以有许多子女,从几个到几千个不等,一个B树结点可以拥有的子女数是由磁盘页的大小所决定,这是因为一个结点的大小通常相当于一个完整的磁盘页。磁盘存取次数是按需要从盘中读出或向盘中写入的信息的页数来度量的,所以,存取磁盘的总时间可以近似为读或写的页数。因此,B树一般都选择大的分支因子,这样可以大大降低树的高度,以及寻找任意关键字所需的磁盘存取次数。一棵分支因子为1001, 高度为2的B树,可以储存超过10亿个关键字,同时因为根节点可以持久地保留在内存中,故在这棵树中,寻找一个关键字至多只需要两次磁盘存取。

相信,从上图你能轻易的看到,一个内结点x若含有n[x]个关键字,那么x将含有n[x]+1个子女。如含有2个关键字D H的内结点有3个子女,而含有3个关键字Q T X的内结点有4个子女。
B树的性质:
1) 每个节点x的域:
a) n[x],x中的关键字数,若x是B树中的内节点,则x有n[x] + 1个子女。
b) n[x]个关键字本身,以非降序排列,key1[x] <= key2[x] <= … <= keyn[x][x]
c) leaf[x],布尔值,如果x是叶节点,则为TRUE,若为内节点,则为FALSE
2) 每个内节点x还包含n[x] + 1个指向其子女的指针c1[x], c2[x], …, cn[x] + 1[x]
3) 如果ki为存储在以ci[x]为根的子树中的关键字,则k1 <= key1[x] <= k2 <= key2[x] <= … <= keyn[x][x] <= keyn[x] + 1
4) 每个叶节点具有相同的深度
5) B树的最小度数t
a) 每个非根的节点必须至少有t – 1个关键字
b) 每个节点可包含至多2t – 1个关键字。
B树的数据结构:
B树插入关键字
B树插入是指插入到一个已知的叶节点上,因为不能把关键字插入到一个满的叶结点上,故引入一个操作,将一个满的结点y(有2t – 1个关键字)按其中间关键字key[y]分裂成两个各含t – 1个关键字的节点,中间关键字提升到y的双亲结点,如果y的双亲也是满的,则自底向上传播分裂。
如同二叉查找树,插入时,需要从根部沿着树下降到叶子,当沿着树往下查找新关键字所属位置时,就分裂遇到的每一个满结点,这样就能保证,要分裂一个满结点y时,就能确保它的双亲不是满的。
分裂图示:
插入结点伪代码:
B-TREE-INSERT(T, k)作用是对B树用单程下行遍历方式插入关键字。3~9行处理根结点r为满的情况。
B-TREE-SPLIT-CHILD(x, i, y) 第1~8行行创建一个新结点,并将y的t – 1个最大关键字以及相应的t个子女给它,第九行调整关键字计数。第10~16行将z插入为x的一个孩子,提升y的中间关键字到x来分裂y和z,并调整x的关键字计数。
B-TREE-INSERT-NONFULL(x, k) 第3~8行处理x是叶子的情况,将关键字k插入x;如果不是,则第9~11确定向x的哪个子结点递归下降。第13行检查递归是否将降至一个满子结点上,若是,14行用B-TREE-SPLIT-CHILD将该子结点分类成两个非满的孩子,第15~16行确定向两个孩子中的哪一个下降是正确的。
各种情况都包含的插入图示:(最小度数t为3)
3)删除操作:
书上没有给出伪代码,只给出了基本思路,设关键字为k,x为节点
1) 若k在x中,且x是叶节点,则从x中删除k
2) 若k在x中,且x是内节点,则
a) 若x中前于k的子节点y包含至少t个关键字,则找出k在以y为根的子树中的前驱k’。递归地删除k’,并在x中用k’取代k。
b) 若x中后于k的子节点z包含至少t个关键字,则找出k在以z为根的子树中的后继k’。递归地删除k’,并在x中用k’取代k。
c) 否则,将k和z所有关键字合并进y,然后,释放z并将k从y中递归删除。
3) 若k不在x中,则确定必包含k的正确的子树的根ci[x]。若ci[x]只有t – 1个关键字,则执行a或b操作。然后,对合适的子节点递归删除k。
a) 若ci[x]只包含t-1个关键字,但它的相邻兄弟包含至少t个关键字,则将x中的某一个关键字降至ci[x],将ci[x]的相邻兄弟中的某一个关键字升至x,将该兄弟中合适的子女指针迁移到ci[x]中。
b) 若ci[x]与其所有相邻兄弟节点都包含t-1个关键字,则将ci[x]与一个兄弟合并,将x的一个关键字移至新合并的节点。
删除结点图示:(最小度数为2)
完整实现代码:
/*
按关键字的顺序遍历B-树:
(3, 11)
(7, 16)
(12, 4)
(24, 1)
(26, 13)
(30, 12)
(37, 5)
(45, 2)
(50, 6)
(53, 3)
(61, 7)
(70, 10)
(85, 14)
(90, 8)
(100, 9)
请输入待查找记录的关键字: 26
(26, 13)
5
没找到
37
(37, 5)
*/
#include
#include
#include
#include
using namespace std;
#define m 3 // B树的阶,暂设为3
//3阶的B-数上所有非终点结点至多可以有两个关键字
#define N 16 // 数据元素个数
#define MAX 5 // 字符串最大长度 + 1
//记录类型
struct Record{
int key; // 关键字
char info[MAX];
};
//B-树ADT
struct BTreeNode {
int keynum; // 结点中关键字个数
struct BTreeNode * parent; // 指向双亲结点
struct Node { // 结点类型
int key; // 关键字
Record * recptr; // 记录指针
struct BTreeNode * ptr; // 子树指针
}node[m + 1]; // key, recptr的0号单元未用
};
typedef BTreeNode BT;
typedef BTreeNode * Position;
typedef BTreeNode * SearchTree;
//B-树查找结果的类型
typedef struct {
Position pt; // 指向找到的结点
int i; // 1..m,在结点中的关键字序号
int tag; // 1:查找成功,O:查找失败
}Result;
inline void print(BT c, int i) {// TraverseSearchTree()调用的函数
printf("(%d, %s)\n", c.node[i].key, c.node[i].recptr->info);
}
//销毁查找树
void DestroySearchTree(SearchTree tree) {
if(tree) {// 非空树
for(int i = 0; i <= (tree)->keynum; i++ ) {
DestroySearchTree(tree->node[i].ptr); // 依次销毁第i棵子树
}
free(tree); // 释放根结点
tree = NULL; // 空指针赋0
}
}
//在p->node[1..keynum].key中查找i, 使得p->node[i].key≤K<p->node[i + 1].key
//返回刚好小于等于K的位置
int Search(Position p, int K) {
int location = 0;
for(int i = 1; i <= p->keynum; i++ ) {
if(p->node[i].key <= K) {
location = i;
}
}
return location;
}
/*
在m阶B树tree上查找关键字K,返回结果(pt, i, tag)。
若查找成功,tag = 1,指针pt所指结点中第i个关键字等于K;
若查找失败,tag = 0,等于K的关键字应插入在指针Pt所指结点中第i和第i + 1个关键字之间。
*/
Result SearchPosition(SearchTree tree, int K) {
Position p = tree, q = NULL; // 初始化,p指向待查结点,q指向p的双亲
bool found = false;
int i = 0;
Result r;
while(p && !found) {
i = Search(p, K); // p->node[i].key≤Knode[i + 1].key
if(i > 0 && p->node[i].key == K) {// 找到待查关键字
found = true;
} else {
q = p;
p = p->node[i].ptr;
}
}
r.i = i;
if(found) {// 查找成功
r.pt = p;
r.tag = 1;
} else {// 查找不成功,返回K的插入位置信息
r.pt = q;
r.tag = 0;
}
return r;
}
//将r->key、r和ap分别插入到q->key[i + 1]、q->recptr[i + 1]和q->ptr[i + 1]中
void Insert(Position q, int i, Record * r, Position ap) {
for(int j = q->keynum; j > i; j--) {// 空出q->node[i + 1]
q->node[j + 1] = q->node[j];
}
q->node[i + 1].key = r->key;
q->node[i + 1].ptr = ap;
q->node[i + 1].recptr = r;
q->keynum++;
}
// 将结点q分裂成两个结点,前一半保留,后一半移入新生结点ap
void split(Position &q, Position &ap) {
int s = (m + 1) / 2;
ap = (Position)malloc(sizeof(BT)); // 生成新结点ap
ap->node[0].ptr = q->node[s].ptr; // 后一半移入ap
for(int i = s + 1; i <= m; i++ ) {
ap->node[i-s] = q->node[i];
if(ap->node[i - s].ptr) {
ap->node[i - s].ptr->parent = ap;
}
}
ap->keynum = m - s;
ap->parent = q->parent;
q->keynum = s - 1; // q的前一半保留,修改keynum
}
// 生成含信息(T, r, ap)的新的根结点*T,原T和ap为子树指针
void NewRoot(Position &tree, Record *r, Position ap) {
Position p;
p = (Position)malloc(sizeof(BT));
p->node[0].ptr = tree;
tree = p;
if(tree->node[0].ptr) {
tree->node[0].ptr->parent = tree;
}
tree->parent = NULL;
tree->keynum = 1;
tree->node[1].key = r->key;
tree->node[1].recptr = r;
tree->node[1].ptr = ap;
if(tree->node[1].ptr) {
tree->node[1].ptr->parent = tree;
}
}
/*
在m阶B-树tree上结点*q的key[i]与key[i + 1]之间插入关键字K的指针r。若引起
结点过大, 则沿双亲链进行必要的结点分裂调整, 使tree仍是m阶B树。
*/
void InsertPosition(SearchTree &tree, Record &r, Position q, int i) {
Position ap = NULL;
bool finished = false;
Record *rx = &r;
while(q && !finished) {
// 将r->key、r和ap分别插入到q->key[i + 1]、q->recptr[i + 1]和q->ptr[i + 1]中
Insert(q, i, rx, ap);
if(q->keynum < m) {
finished = true; // 插入完成
} else { // 分裂结点*q
int s = (m + 1) >> 1;
rx = q->node[s].recptr;
// 将q->key[s + 1..m], q->ptr[s..m]和q->recptr[s + 1..m]移入新结点*ap
split(q, ap);
q = q->parent;
if(q) {
i = Search(q, rx->key); // 在双亲结点*q中查找rx->key的插入位置
}
}
}
if(!finished) {// T是空树(参数q初值为NULL)或根结点已分裂为结点*q和*ap
NewRoot(tree, rx, ap); // 生成含信息(T, rx, ap)的新的根结点*T,原T和ap为子树指针
}
}
/*
操作结果: 按关键字的顺序对tree的每个结点调用函数Visit()一次且至多一次
*/
void TraverseSearchTree(SearchTree tree, void(*Visit)(BT, int)) {
if(tree) {// 非空树
if(tree->node[0].ptr) {// 有第0棵子树
TraverseSearchTree(tree->node[0].ptr, Visit);
}
for(int i = 1; i <= tree->keynum; i++ ) {
Visit(*tree, i);
if(tree->node[i].ptr) { // 有第i棵子树
TraverseSearchTree(tree->node[i].ptr, Visit);
}
}
}
}
int main() {
Record r[N] = {{24, "1"}, {45, "2"}, {53, "3"}, {12, "4"},
{37, "5"}, {50, "6"}, {61, "7"}, {90, "8"},
{100, "9"}, {70, "10"}, {3, "11"}, {30, "12"},
{26, "13"}, {85, "14"}, {3, "15"}, {7, "16"}};
SearchTree tree = NULL;//初始化一棵空树
Result res;//存放结果
int i;
for(i = 0; i < N; i++ ) {
res = SearchPosition(tree, r[i].key);
if(!res.tag) {
InsertPosition(tree, r[i], res.pt, res.i);
}
}
printf("按关键字的顺序遍历B-树:\n");
TraverseSearchTree(tree, print);
printf("\n请输入待查找记录的关键字: ");
while (scanf("%d", &i)) {
res = SearchPosition(tree, i);
if(res.tag) {
print(*(res.pt), res.i);
} else {
printf("没找到\n");
}
puts("");
}
DestroySearchTree(tree);
}
B+-tree:是应文件系统所需而产生的一种B-tree的变形树。
一棵m阶的B+树和m阶的B树的差异在于:
1.有n棵子树的结点中含有n个关键字; (而B 树是n棵子树有n-1个关键字)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)

a) 为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引?
1) B+-tree的磁盘读写代价更低
B+-tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
举个例子,假设磁盘中的一个盘块容纳16bytes,而一个关键字2bytes,一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候,B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
2) B+-tree的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
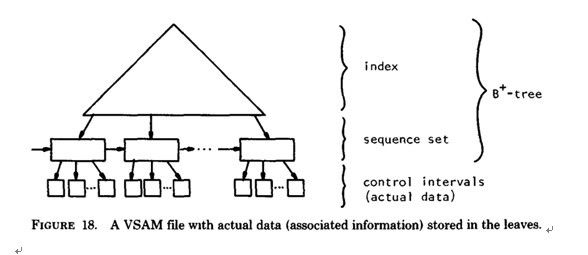
b) B+-tree的应用: VSAM(虚拟存储存取法)文件(来源论文 the ubiquitous Btree 作者:D COMER - 1979 )
5.B*-tree
B*-tree是B+-tree的变体,在B+ 树非根和非叶子结点再增加指向兄弟的指针;B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2)。给出了一个简单实例,如下图所示:
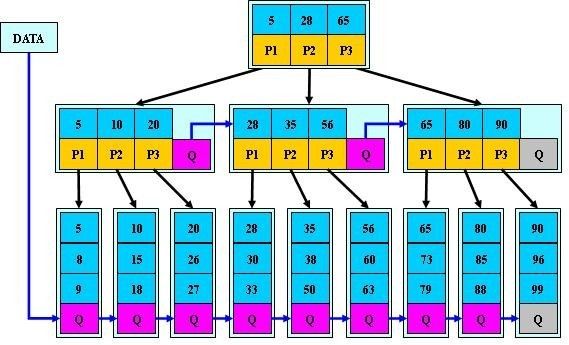
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
二,B+树
B+树:是应文件系统所需而产生的一种B-的变形树。
一棵m阶的B+树和m阶的B树的差异在于:
1.有n棵子树的结点中含有n个关键字; (而B 树是n棵子树有n-1个关键字)
2.所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键字。 (而B 树的非终节点也包含需要查找的有效信息)

a) 为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引?
1) B+-tree的磁盘读写代价更低
B+-tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
举个例子,假设磁盘中的一个盘块容纳16bytes,而一个关键字2bytes,一个关键字具体信息指针2bytes。一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候,B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。
2) B+-tree的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
B-树:
B+树:
5.B*-tree
B*-tree是B+-tree的变体,在B+ 树非根和非叶子结点再增加指向兄弟的指针;B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2)。给出了一个简单实例,如下图所示:

B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针。
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针。
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
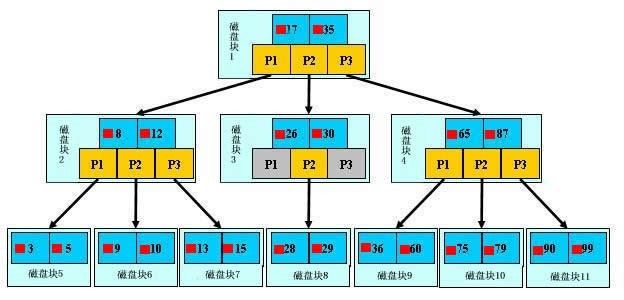
在大规模数据存储的文件系统中,B~tree系列数据结构,起着很重要的作用,对于存储不同的数据,节点相关的信息也是有所不同,这里根据自己的理解,画的一个查找以职工号为关键字,职工号为38的记录的简单示意图。(这里假设每个物理块容纳3个索引,磁盘的I/O操作的基本单位是块(block),磁盘访问很费时,采用B+树有效的减少了访问磁盘的次数。)
对于像MySQL,DB2,Oracle等数据库中的索引结构得有较深入的了解才行,建议去找一些B 树相关的开源代码研究。

三,R树的数据结构
如上所述,R树是B树在高维空间的扩展,是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针,这些数据可以是存放在硬盘中的,也可以是存在内存中。根据R树的这种数据结构,当我们需要进行一个高维空间查询时,我们只需要遍历少数几个叶子结点所包含的指针,查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案,效率显著提高。下图1是R树的一个简单实例:

我们在上面说过,R树运用了空间分割的理念,这种理念是如何实现的呢?R树采用了一种称为MBR(Minimal Bounding Rectangle)的方法,在此我把它译作“最小边界矩形”。从叶子结点开始用矩形(rectangle)将空间框起来,结点越往上,框住的空间就越大,以此对空间进行分割。有点不懂?没关系,继续往下看。在这里我还想提一下,R树中的R应该代表的是Rectangle(此处参考wikipedia),而不是大多数国内教材中所说的Region(很多书把R树称为区域树,这是有误的)。我们就拿二维空间来举例吧。下图是Guttman论文中的一幅图。
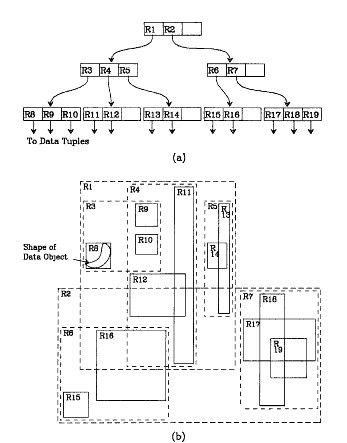
我来详细解释一下这张图。先来看图(b)吧。首先我们假设所有数据都是二维空间下的点,图中仅仅标志了R8区域中的数据,也就是那个shape of data object。别把那一块不规则图形看成一个数据,我们把它看作是多个数据围成的一个区域。为了实现R树结构,我们用一个最小边界矩形恰好框住这个不规则区域,这样,我们就构造出了一个区域:R8。R8的特点很明显,就是正正好好框住所有在此区域中的数据。其他实线包围住的区域,如R9,R10,R12等都是同样的道理。这样一来,我们一共得到了12个最最基本的最小矩形。这些矩形都将被存储在子结点中。下一步操作就是进行高一层次的处理。我们发现R8,R9,R10三个矩形距离最为靠近,因此就可以用一个更大的矩形R3恰好框住这3个矩形。同样道理,R15,R16被R6恰好框住,R11,R12被R4恰好框住,等等。所有最基本的最小边界矩形被框入更大的矩形中之后,再次迭代,用更大的框去框住这些矩形。我想大家都应该理解这个数据结构的特征了。用地图的例子来解释,就是所有的数据都是餐厅所对应的地点,先把相邻的餐厅划分到同一块区域,划分好所有餐厅之后,再把邻近的区域划分到更大的区域,划分完毕后再次进行更高层次的划分,直到划分到只剩下两个最大的区域为止。要查找的时候就方便了吧。
有关R树的详细介绍请看博文http://blog.csdn.net/v_july_v/article/details/6530142
![]()
![]()
![]()
![]()
![]()
![]()
![]()