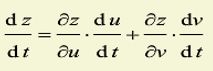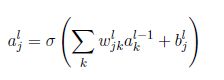5月深度学习班第3课梯度下降法与反向传播

梯度下降法与反向传播

 

梯度下降法
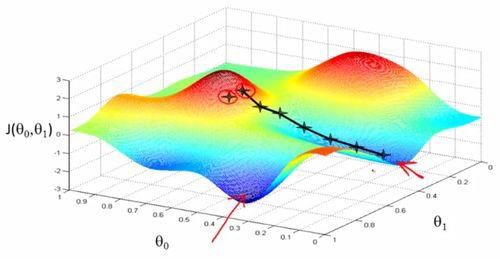
1.损失函数可视化
2.最优化
3.梯度下降
反向传播
1.梯度与偏导
2.链式法则
3.直观理解
4.Sigmoid例子

 

两个重要函数
得分函数
损失函数
核心目标
找到最合适的参数w.
使得损失函数取值最小化。
也就是最优化的过程

 

损失函数往往定义在非常高维的空间
比如CIFAR-10的例子里一个线性分类器的权重矩阵W是10 x 3073维的，总共有30730个参数
曲线救国
我们可以把高维投射到一个向量/方向(1维)或者一个面(2维)上，从而能直观地『观察』到一些变化

 

假定训练集里面有3个样本，都是1维的，同时总共有3个类别。其SVM损失：

凸优化
SVM损失函数是一个凸函数。
凸函数的正系数加和仍然是凸函数。
但扩充到神经网络之后，损失函数将变成一个非凸函数

 

最优化

策略1：随机搜寻(不太实用)
最直接粗暴的方法就是，我们尽量多地去试参数，然后从里面选那个让损失函数最小的，作为最后的W。

 

策略2：随机局部搜索
在现有的参数W基础上，搜寻一下周边临近的参数，有没有比现在参数更好的W，然后我们用新的W替换现在的W，不断迭代。

 

策略3：顺着梯度下滑
找到最陡的方向，迈一小步，然后再找当前位置最陡的下山方向，再迈一小步…

 

计算梯度
关于迭代的步长：
步子迈得太小，时间耗不起。
步子迈得太大，容易来回震荡……

 

关于效率问题：
这个计算方法的复杂度，基本是和我们的参数个数成线性关系的。
在CIFAR-10例子中，我们总共有30730个参数
这个问题在神经网络中更为严重，很可能两层神经元之间就有百万级别的参数权重。
人也要等结果等到哭瞎…

 

 

解析法计算梯度：
速度非常快
但是容易出错
反倒之前的数值法就显出优势。
我们可以先计算解析梯度和数值梯度，然后比对结果和校正，然后就可以大胆地进行解析法计算了
这个过程叫做梯度检查/检测

 

 一个样本点的SVM损失函数：

 

梯度下降
这个简单的循环就是很多神经网络库的核心：

 

Mini-batch：
对整个训练数据集的样本都算一遍损失函数，以完成参数迭代是一件非常耗时的事情，一个我们通常会用到的替代方法是，采样出一个子集在其上计算梯度。

 

 

 第二部分：反向传播

偏导与梯度的关系
链式法则：

 

Sigmoid函数的导数可以用自己很简单的重新表示出来(非常重要)：

 

74行代码实现手写数字识别

 

转载于:https://www.cnblogs.com/koocn/p/7754375.html