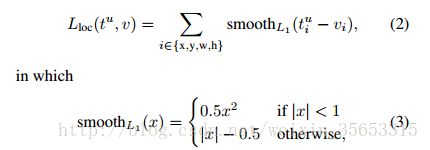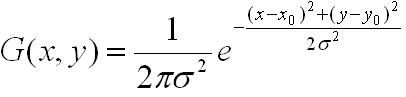卷积
1x1卷积核的作用
- 实现跨通道的交互和信息整合
- 进行卷积核通道数的降维和升维
- 加入非线性。卷积层之后经过激励层,1*1的卷积在前一层的学习表示上添加了非线性激励( non-linear activation ),提升网络的表达能力
为什么3x3卷积核
- 两个3x3的堆叠卷基层的有限感受野是5x5;三个3x3的堆叠卷基层的感受野是7x7,故可以通过小尺寸卷积层的堆叠替代大尺寸卷积层,并且感受野大小不变。多个3x3的卷基层比一个大尺寸filter卷基层有更多的非线性(更多层的非线性函数),使得判决函数更加具有判决性。
- 多个3x3的卷积层比一个大尺寸的filter有更少的参数,假设卷基层的输入和输出的特征图大小相同为C,那么三个3x3的卷积层参数个数3x(3x3xCxC)=27C2;一个7x7的卷积层参数为49C2;所以可以把三个3x3的filter看成是一个7x7filter的分解(中间层有非线性的分解, 并且起到隐式正则化的作用。
mobilenet中depthwise卷积的作用和优势
- 深度卷积是对输入的每一个channel独立的用对应channel的所有卷积核去卷积,在深度卷积后面又加了pointwise convolution,这个pointwise convolution就是1*1的卷积,可以看做是对那么多分离的通道做了个融合。
- 与标准卷积相比,这种分离式卷积大大降低了计算量。
空洞卷积
- pooling的缺点:pooling下采样操作导致的信息丢失是不可逆的,内部数据结构丢失,空间层级化信息丢失,小物体信息无法重建 (假设有四个pooling layer 则 任何小于 2^4 = 16 pixel 的物体信息将理论上无法重建。)
- 又叫dilation卷积,通常的分类识别模型,只需要预测每一类的概率,所以我们不需要考虑pooling会导致损失图像细节信息的问题,但是做像素级的预测时(譬如语义分割),就要考虑到这个问题了。所以就要有一种卷积代替pooling的作用(成倍的增加感受野),而空洞卷积就是为了做这个的。通过卷积核插“0”的方式,它可以比普通的卷积获得更大的感受野。
训练&优化
反向传播&梯度
梯度消失,梯度爆炸是什么
- 从深层网络角度来讲,不同的层学习的速度差异很大,表现为网络中靠近输出的层学习的情况很好,靠近输入的层学习的很慢,有时甚至训练了很久,前几层的权值和刚开始随机初始化的值差不多。因此,梯度消失、爆炸,其根本原因在于反向传播训练法则,属于先天不足。
- 激活函数选择不合适,比如使用sigmoid,梯度消失就会很明显。
- 梯度爆炸就是由于初始化权值过大,前面层会比后面层变化的更快,就会导致权值越来越大,梯度爆炸的现象就发生了。在深层网络或循环神经网络中,误差梯度可在更新中累积,变成非常大的梯度,然后导致网络权重的大幅更新,并因此使网络变得不稳定。在极端情况下,权重的值变得非常大,以至于溢出,导致 NaN 值。
梯度消失,梯度爆炸怎么解决
- 梯度剪切这个方案主要是针对梯度爆炸提出的,其思想是设置一个梯度剪切阈值,然后更新梯度的时候,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
- 权重正则化(weithts regularization)比较常见的是l1正则,和l2正则。
- 使用relu、leakrelu、elu等激活函数,激活后导数不会很小。
- batchnorm:W的大小影响了梯度的消失和爆炸,batchnorm就是通过对每一层的输出规范为均值和方差一致的方法,消除了w带来的放大缩小的影响,
- 残差结构:拟合残差,short-cut完整的梯度信息(接近1)
卷积中的反向传播推导
TODO
损失函数
SoftMax Loss
- 计算与标注样本的差距,取log里面的值就是这组数据正确分类的Softmax值,它占的比重越大,这个样本的Loss也就越小.
- 计算上非常非常的方便,对权重矩阵求偏导最后结果的形式非常的简单,只要将算出来的概率的向量对应的真正结果的那一维减1,就可以了。
推导过程比较简单,主要分i==j和i!=j这两种情况
Smooth L1 Loss
- 使用l2 loss时,当预测值与目标值相差很大时, 梯度容易爆炸, 因为梯度里包含了x−t.使用Smooth L1 Loss,对噪声(outliers)更鲁棒。
Focal Loss
针对Single stage detector目标检测来说,存在以下几个问题:
- 极度不平衡的正负样本比例: anchor近似于sliding window的方式会使正负样本接近1000:1,而且绝大部分负样本都是easy example
- gradient被easy example dominant的问题:往往这些easy example虽然loss很低,但由于数 量众多,对于loss依旧有很大贡献,从而导致收敛到不够好的一个结果。
提出了focal loss来解决imbalanced样本问题,将predictions作为example的难易反馈整合到loss中,在每次迭代中都能够自适应地鉴别样本的“难”还是“易”,从而让模型在后期尽量去学习那些hard example。
Like the focal loss,OHEM puts more emphasis on misclassified examples, but unlike FL, OHEM completely discards easy examples
优化算法
SGD
梯度下降法每进行一次 迭代 都需要将所有的样本进行计算,当样本量十分大的时候,会非常消耗计算资源,收敛速度会很慢。逐个样本进行loss计算进行迭代的方法,称之为 Stochasitc Gradient Descent 简称SGD。而这样会导致loss波动很大,不稳定,因而提出 mini-batch gradient descent,每次计算一个小batch。波动的减小还是比较明显。同时收敛的速度也是大大加快。
缺点:
- 对学习率的选择非常敏感,还需要根据数据集的特点来预先定义好学习率的衰减过程
- 对所有参数使用相同的学习率更新,这样的话对于稀疏和低频特征来说,不能实现对罕见特征的更大幅度更新。
- 优化很容易陷入鞍点,而鞍点周围误差变化不大,从而在所有维度上的梯度都为0,SGD很难逃出鞍点范围。
Momentum
将之前梯度下降方向考虑到当前的梯度,梯度需要有一个衰减值γ ,推荐取0.9。这样的做法可以让早期的梯度对当前梯度的影响越来越小,如果没有衰减值,模型往往会震荡难以收敛,甚至发散。
Adagrad
上述方法中,对于每一个参数θi 的训练都使用了相同的学习率α。Adagrad算法能够在训练中自动的对learning rate进行调整,对于出现频率较低参数采用较大的α更新;相反,对于出现频率较高的参数采用较小的α更新。因此,Adagrad非常适合处理稀疏数据。缺点是在训练的中后期,分母上梯度平方的累加将会越来越大,从而梯度趋近于0,使得训练提前结束。
RMSprop
Adagrad会累加之前所有的梯度平方,而RMSprop仅仅是计算对应的平均值,因此可缓解Adagrad算法学习率下降较快的问题。
Adam
Adam(Adaptive Moment Estimation)是另一种自适应学习率的方法。它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。
Q&A
在深度学习中,模型和数据量之间的关系
- 一般来说模型越大,需要的数据量越大
- 但是数据质量比数量重要,大量同源数据对模型的效果并不大,特别是样本不均衡的情况
- 差异性越大的数据,越能表现原始数据分布的情况,对模型效果提升可能有作用
如何提高深度学习的可解释性
深度学习中的指标mAP等(衡量模型好坏的指标?)平均精度(mAP)如何计算的
传统机器学习上,召回率和准确率定义如下
- 召回率 Recall = TP / (TP + FN)
- 准确率 Precision = TP / (TP + FP)
在机器视觉目标检测领域也是一样的,recall和precision只是分母抽样的方式不同,计算过程如下:
- 首先计算C在一张图片上的Precision=在一张图片上类别C识别正确的个数(也就是IoU>0.5)/一张图片上类别C的总个数
- 依然对于某个类别C,可能在多张图片上有该类别,下面计算类别C的AP指数:AP=每张图片上的Precision求和/含有类别C的图片数目
- 对于整个数据集,存在多个类别C1、C2、C3:mAP=上一步计算的所有类别的AP和/总的类别数目,相当于所有类别的AP的平均值
类似对不同IOU threshold(如0.75等)有同样的[email protected]
分类问题为什么要用交叉熵做loss函数,而不是mse
当我们进行分类任务的时候,我们的目标常常是分错样本越少越好,也就是零一损失。但是零一损失很难计算。我们就寻找一些可以进行计算的损失函数来替代零一损失。也就是说我们把原来的优化问题转化为一个近似的优化问题。不同的ssurrogate loss function对应着不同的优化问题,就有着不同的优化目标和优化方法,也就从本质上定义了不同类型的分类器。当我们用hinge loss做surrogate loss function去找一个线性分类器的时候,实际上我们就是用的SVM。当我们用logloss作为surrogate loss function去求解一个线性分类器的时候,实际上我们的模型就是LogisticsRegression。这个替身我们就称作surrogate loss function代理损失函数。
当我们把原来的零一损失函数替代为其他损失函数的时候,我们自然会问,当我们对代理损失函数进行优化的时候,原来的零一损失是否也被最小化了?它们的差距是多少呢?如果最优化代理损失函数的同时我们也最优化了原本的损失函数,我们就称校对性(calibration)或者一致性(consistency)。这个性质与我们所选择的代理损失函数相关。一个重要的定理是,如果代理损失函数是凸函数,并且在0点可导,其导数小于0,那么它一定是具有一致性的。这也是为什么我们通常选择凸函数作为我们的loss function的原因之一。如果用 MSE 计算softmax结果的 loss, 输出的曲线是非凸的,有很多局部的极值点。即,非凸优化问题 (non-convex)。
什么样的资料集不适合用深度学习?
- 数据集太小,数据样本不足时,深度学习相对其它机器学习算法,没有明显优势。
- 数据集没有局部相关特性,目前深度学习表现比较好的领域主要是图像/语音/自然语言处理等领域,这些领域的一个共性是局部相关性。图像中像素组成物体,语音信号中音位组合成单词,文本数据中单词组合成句子,这些特征元素的组合一旦被打乱,表示的含义同时也被改变。对于没有这样的局部相关性的数据集,不适于使用深度学习算法进行处理。举个例子:预测一个人的健康状况,相关的参数会有年龄、职业、收入、家庭状况等各种元素,将这些元素打乱,并不会影响相关的结果。
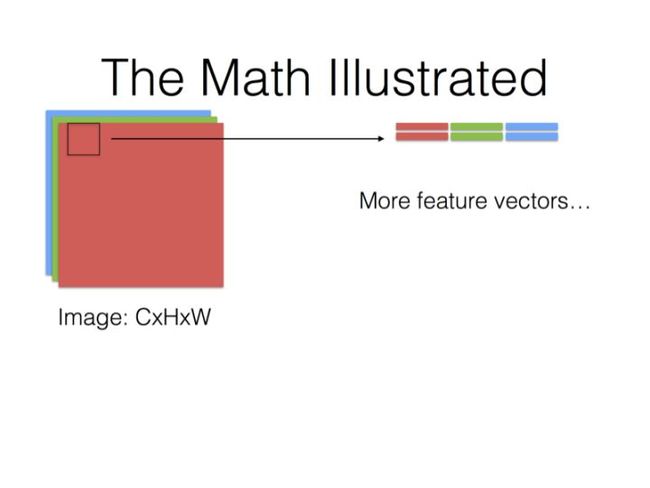
im2col原理
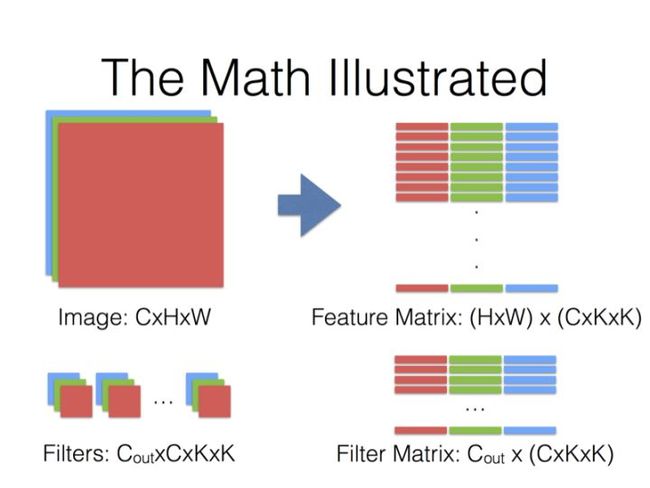
caffe中的卷积使用im2col以及sgemm方式实现,im2col如下图所示:
- 优点:逻辑简单,实现容易
- 缺点:需要大量的内存开销
最后一步就是,Filter Matrix乘以Feature Matrix的转置,得到输出矩阵Cout x (H x W),就可以解释为输出的三维Blob(Cout x H x W)。
激活函数的选取
-
relu:
-
缺点:在(-)部分相当于神经元死亡而且不会复活
-
优点:线性运算收敛速度更快,解决了部分梯度弥散问题
-
-
Leaky relu:
- 优点:解决了relu中死亡神经元的问题
-
tanh
-
缺点:梯度消失问题依然存在
-
优点:解决了原点对称问题,比sigmoid更快
-
-
sigmoid
- 缺点:梯度消失,函数输出不是以0为中心的,这样会使权重更新效率降低,sigmod函数要进行指数运算,这个对于计算机来说是比较慢的。
名词解释
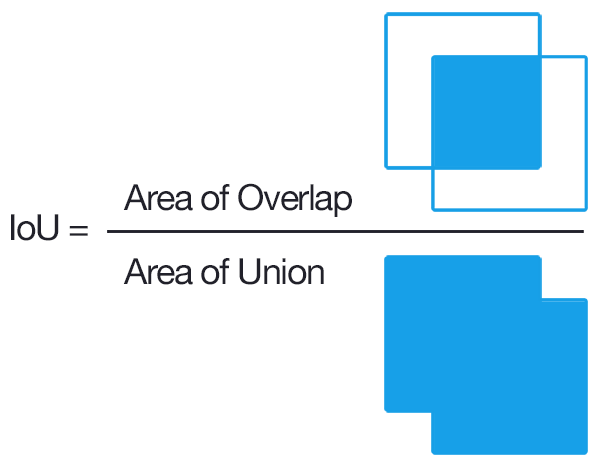
IoU
Intersection over Union,交集并集比。
ROC
ROC受试者工作特征曲线。理解之前我们先要回顾一下真阳率(TP),假阳率(FP),假阴率(FN),真阴率(TN)的概念:
接下来我们考虑ROC曲线图中的四个点和一条线。第一个点,(0,1),即FPR=0, TPR=1,这意味着FN(false negative)=0,并且FP(false positive)=0。Wow,这是一个完美的分类器,它将所有的样本都正确分类。第二个点,(1,0),即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因为它成功避开了所有的正确答案。第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP(true positive)=0,可以发现该分类器预测所有的样本都为负样本(negative)。类似的,第四个点(1,1),分类器实际上预测所有的样本都为正样本。经过以上的分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好。
我们从高到低,依次将分类器s输出“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
- 当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变,特别适合正负样本不均衡的情况
AUC
AUC值是一个概率值,当你随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然,AUC值越大,当前的分类算法越有可能将正样本排在负样本前面,即能够更好的分类。
HOG
梯度直方图(Histogram of Gradient),计算过程如下:
- 标准化gamma空间和颜色空间。为了减少光照因素的影响,首先需要将整个图像进行规范化(归一化),这种压缩处理能够有效地降低图像局部的阴影和光照变化。
- 对于灰度图像,一般为了去除噪点,所以会先利用离散高斯平滑模板进行平滑:高斯函数在不同平滑的尺度下进行对灰度图像进行平滑操作。
- 如下图,计算图像梯度:式中Gx(x,y),Gy(x,y)分别表示输入图像在像素点(x,y)处的水平方向梯度和垂直方向梯度。则G(x,y),α(x,y)分别为像素点(x,y)的梯度幅值和梯度方向。首先用[-1,0,1]梯度算子对原图像做卷积运算,得到水平方向(以向右为正方向)的梯度分量,然后用[1,0,-1]T梯度算子对原图像做卷积运算,得到竖直方向(以向上为正方向)的梯度分量。
- 将图像分成若干个“单元格cell”,例如每个cell为8X8的像素大小。假设采用9个bin的直方图来统计这8X8个像素的梯度信息,即将cell的梯度方向0~180度(或0~360度,考虑了正负,signed)分成9个方向块。如下图所示:如果这个像素的梯度方向是20-40度,直方图第2个bin即的计数就加1,这样,对cell内每个像素用梯度方向在直方图中进行加权投影,将其映射到对应的角度范围块内,就可以得到这个cell的梯度方向直方图了,就是该cell对应的9维特征向量(因为有9个bin)。这边的加权投影所用的权值为当前点的梯度幅值。例如说:某个像素的梯度方向是在,其梯度幅值是4,那么直方图第2个bin的计数就不是加1了,而是加4。这样就得到关于梯度方向的一个加权直方图。
- 各个细胞单元组合成大的、空间上连通的区域(blocks)。这样,一个block内所有cell的特征向量串联起来便得到该block的HOG特征。这些区间是互有重叠的,这就意味着:每一个单元格的特征会以不同的结果多次出现在最后的特征向量中。
如上图,一般一个块(Block)都由若干单元(Cell)组成,一个单元都有如干个像素点组成。 假设参数设置是:2×2 cell/block、8×8像素/cell、9个直方图通道(9bins),一个块的特征向量长度为:2×2×9。对block块内的HOG特征向量进行归一化。一般采用的归一化函数有L2-norm
- 最后将HOG送入一个svm分类器做训练,特征维度如下得到:
- detection window:64×128;
- 8×8 pixels/cell; bin=9; 2×2cells/block;
- blockstride=1cell; 参考卷积stride
- block number:15×7=105;参考卷积中的 VALID方式
- Length of HOG feature vector: 2×2×9×15×7=3780,最后就是把这么一个3780维的特征向量输入给SVM做训练分类。
综上,HOG具有以下优点:
- 核心思想是所检测的局部物体外形能够被梯度或边缘方向的分布所描述,HOG能较好地捕捉局部形状信息,对几何和光学变化都有很好的不变性;
- HOG是在密集采样的图像块中求取的,在计算得到的HOG特征向量中隐含了该块与检测窗口之间的空间位置关系。
但是,HOG的缺点如下:
- 很难处理遮挡问题,人体姿势动作幅度过大或物体方向改变也不易检测
- 跟SIFT相比,HOG没有选取主方向,也没有旋转梯度方向直方图,因而本身不具有旋转不变性(较大的方向变化),其旋转不变性是通过采用不同旋转方向的训练样本来实现的
- 跟SIFT相比,HOG本身不具有尺度不变性,其尺度不变性是通过缩放检测窗口图像的大小来实现的
- 由于梯度的性质,HOG对噪点相当敏感,在实际应用中,在Block和Cell划分之后,对于得到各个像区域中,有时候还会做一次高斯平滑去除噪点
图像金字塔
图像金字塔是一种以多分辨率来解释图像的结构,通过对原始图像进行多尺度像素采样的方式,生成N个不同分辨率的图像。获得图像金字塔一般包括二个步骤:
- 利用低通滤波器平滑图像
- 对平滑图像进行抽样(采样),两种采样方式:上采样(分辨率逐级升高)和下采样(分辨率逐级降低
高斯金字塔
高斯金字塔式在Sift算子中提出来的概念,首先高斯金字塔并不是一个金字塔,而是有很多组(Octave)金字塔构成,并且每组金字塔都包含若干层(Interval)。
- 先将原图像扩大一倍之后作为高斯金字塔的第1组第1层,将第1组第1层图像经高斯卷积(其实就是高斯平滑或称高斯滤波)之后作为第1组金字塔的第2层,高斯卷积函数为:
- 将σ乘以一个比例系数k,等到一个新的平滑因子σ=k*σ,用它来平滑第1组第2层图像,结果图像作为第3层。
- 如此这般重复,最后得到L层图像,在同一组中,每一层图像的尺寸都是一样的,只是平滑系数不一样。它们对应的平滑系数分别为:0,σ,kσ,k^2σ , k^3σ…… k^(L-2)σ。
- 将第1组倒数第三层图像作比例因子为2的降采样,得到的图像作为第2组的第1层,然后对第2组的第1层图像做平滑因子为σ的高斯平滑,得到第2组的第2层,就像步骤2中一样,如此得到第2组的L层图像,同组内它们的尺寸是一样的,对应的平滑系数分别为:0,σ,kσ,k2σ,k3σ……k^(L-2)σ。但是在尺寸方面第2组是第1组图像的一半。
这样反复执行,就可以得到一共O组,每组L层,共计O*L个图像,这些图像一起就构成了高斯金字塔:
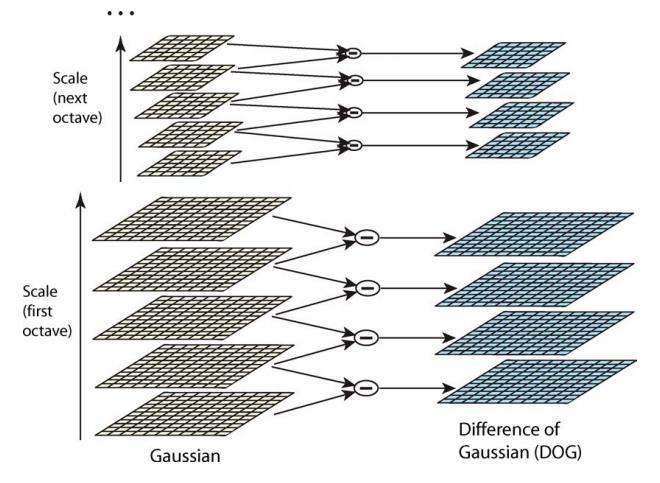
DOG金字塔
DOG(Difference of Gaussian)金字塔是在高斯金字塔的基础上构建起来的,DOG金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。
每一组在层数上,DOG金字塔比高斯金字塔少一层。后续Sift特征点的提取都是在DOG金字塔上进行的。对这些DOG图像进行归一化,可有很明显的看到差分图像所蕴含的特征,并且有一些特征是在不同模糊程度、不同尺度下都存在的,这些特征正是Sift所要提取的“稳定”特征。
SIFT
Scale-invariant feature transform,该算法通过求一幅图中的特征点(interest points,or corner points)及其有关scale 和 orientation 的描述子得到特征并进行图像特征点匹配。
- 构建尺度空间,在高斯金字塔中一共生成O组L层不同尺度的图像,这两个量合起来(O,L)就构成了高斯金字塔的尺度空间
- 为了寻找尺度空间的极值点,每一个采样点要和它所有的相邻点比较,看其是否比它的图像域和尺度域的相邻点大或者小。如图所示,中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。 一个点如果在DOG尺度空间本层以及上下两层的26个领域中是最大或最小值时,就认为该点是图像在该尺度下的一个特征点,如图所示。
- DOG值对噪声和边缘比较敏感,所以在第2步的尺度空间中检测到的局部极值点还要经过进一步的筛选,去除不稳定和错误检测出的极值点。
- 给特征点赋值一个128维方向参数:确定了每幅图中的特征点,为每个特征点计算一个方向,依照这个方向做进一步的计算, 利用关键点邻域像素的梯度方向分布特性为每个关键点指定方向参数,使算子具备旋转不变性。在以关键点为中心的邻域窗口内采样,并用直方图统计邻域像素的梯度方向。梯度直方图的范围是0~360度,其中每45度一个柱,总共8个柱, 或者每10度一个柱,总共36个柱。直方图的峰值则代表了该关键点处邻域梯度的主方向,即作为该关键点的方向。
首先将坐标轴旋转为关键点的方向,以确保旋转不变性。以关键点为中心取8×8的窗口。,图中蓝色的圈代表高斯加权的范围(越靠近关键点的像素梯度方向信息贡献越大)。然后在每4×4的小块上计算8个方向的梯度方向直方图,绘制每个梯度方向的累加值,即可形成一个种子点,如图右部分示。此图中一个关键点由2×2共4个种子点组成,每个种子点有8个方向向量信息。这种邻域方向性信息联合的思想增强了算法抗噪声的能力,同时对于含有定位误差的特征匹配也提供了较好的容错性。
实际应用时计算keypoint周围的16X16的window中每一个像素的梯度,而且使用高斯下降函数降低远离中心的权重。这样就可以对每个feature形成一个4X4X8=128维的描述子,每一维都可以表示4X4个格子中一个的scale/orientation. 将这个向量归一化之后,就进一步去除了光照的影响。
综上,SIFT具有以下优点:
- SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性。
- 独特性好,信息量丰富,适用于在海量特征数据库中进行快速、准确的匹配。
- 多量性,即使少数的几个物体也可以产生大量SIFT特征向量。
- 可扩展性,可以很方便的与其他形式的特征向量进行联合。
Sobel、canny 算子 边缘检测
- Sobel算子
sobel算子的思想,Sobel算子认为,邻域的像素对当前像素产生的影响不是等价的,所以距离不同的像素具有不同的权值,对算子结果产生的影响也不同。一般来说,距离越远,产生的影响越小。 sobel算子的原理,对传进来的图像像素做卷积,卷积的实质是在求梯度值,或者说给了一个加权平均,其中权值就是所谓的卷积核;然后对生成的新像素灰度值做阈值运算,以此来确定边缘信息.Sobel算子包含两组3x3的矩阵,分别为横向及纵向模板,将之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。
优点:计算简单,速度很快;
缺点:计算方向单一,对复杂纹理的情况显得乏力;直接用阈值来判断边缘点欠合理解释,会造成较多的噪声点误判。
haar
自动微分
所有数值计算归根结底是一系列有限的可微算子的组合。自动微分法是一种介于符号微分和数值微分的方法:数值微分(计算量太大)强调一开始直接代入数值近似求解;符号微分(表达式膨胀)强调直接对代数进行求解,最后才代入问题数值;自动微分将符号微分法应用于最基本的算子,比如常数,幂函数,指数函数,对数函数,三角函数等,然后代入数值,保留中间结果,最后再应用于整个函数。