为什么80%的码农都做不了架构师?>>> ![]()
正交分解
矩阵的正交分解又称为QR分解,是将矩阵分解为一个正交矩阵Q和一个上三角矩阵的乘积的形式。
任意实数方阵A,都能被分解为 。这里的Q为正交单位阵,即 R是一个上三角矩阵。这种分解被称为QR分解。 QR分解也有若干种算法,常见的包括Gram–Schmidt、Householder和Givens算法。 QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。用一张图可以形象地表示QR分解: 
为啥我们需要正交分解呢?
实际运用过程中,QR分解经常被用来解线性最小二乘问题,这个问题我们后面讲述。
提到正交分解就不得不讨论(Householder transformation Householder变换)豪斯霍尔德变换和(Schmidt orthogonalization Schmidt正交化)施密特正交化
Schmidt正交化
定理1 设A是n阶实非奇异矩阵,则存在正交矩阵Q和实非奇异上三角矩阵R使A有QR分解;且除去相差一个对角元素的绝对值(模)全等于1的对角矩阵因子外,分解是唯一的.
定理2 设A是m×n实矩阵,且其n个列向量线性无关,则A有分解A=QR,其中Q是m×n实矩阵,且满足QHTQ=E,R是n阶实非奇异上三角矩阵该分解除去相差一个对角元素的绝对值(模)全等于1的对角矩阵因子外是唯一的.用Schmidt正交化分解方法对矩阵进行QR分解时,所论矩阵必须是列满秩矩阵。
算法步骤
- 写出矩阵的列向量;
- 列向量按照Schmidt正交化正交;
- 得出矩阵的Q′,R′;
- 对R′的列向量单位化得到Q,R′的每行乘R′每列的模得푹
matlab代码
function[X,Q,R] = QRSchmidt(A,b)
%方阵的QR的Gram-Schmidt正交化分解法,并用于求解AX=b方程组[m,n]=size(A);
if m~=n
%如果不是方阵,则不满足QR分解要求
disp('不满足QR分解要求');
end
Q=zeros(m,n);
X=zeros(n,1);
R=zeros(n);
for k=1:nR(k,k)=norm(A(:,k));
if R(k,k)==0
break;
end
Q(:,k)=A(:,k)/R(k,k);
for j=k+1:n
R(k,j)=Q(:,k)'*A(:,j);
A(:,j)=A(:,j)-R(k,j)*Q(:,k);
end
if nargin==2
b=Q'* b;
X(n)=b(n)/R(n,n);
for i=n-1:-1:1
X(i)=(b(i)-sum(R(i,i+1:n).*X(i+1:n)'))/R(i,i);
end
else
X=[];
end
end
Householder变换
设A为任一n阶方阵,则必存在n阶酉矩阵Q和n阶上三角阵R,使得A=QR
设w∈Cn是一个单位向量,令
则称H是一个Householder矩阵或Householder变换。则对于任意的存在Householder矩阵H,使得Hx=-au。其中
酉矩阵(unitary matrix)
若n阶复矩阵A满足
则称A为酉矩阵,记之为其中,Ah是A的共轭转置
酉矩阵性质
如果A是酉矩阵
也是酉矩阵;
- det(A)=1;
- 充分条件是它的n个列向量是两两正交的单位向量。
算法步骤
- 将矩阵A按列分块写成A=(α1,α2,...,αn).如果α1≠0,则可得,存在n阶householder矩阵H1使得
于是有
如果α1=0,则直接进行下一步,此时相当于取,而a1=0.
- 将矩阵An-1按列分块写成An-1=(αi,α2,... ,αn-1)。如果α1≠0,则可得,存在n-1阶householder矩阵H’2使得
于是有
此时,令
则H2是n阶Householder矩阵,且使
如果α1=0,则直接进行下一步- 对n-2阶矩阵继续进行类似的变换,如此下去,之多在第n-1步,我们可以找到Householder矩阵H1,H2,...,Hn-1使得
令,则Q是酉矩阵之积,从而必有酉矩阵并且A=QR
matlab代码
function[ X,Q,R ] = QRHouseholder(A,b)
%用Householder变换将方阵A分解为正交Q与上三角矩阵R的乘积,并用于求解AX=b方程组
[n,n]=size(A);
E=eye(n);
X=zeros(n,1);
R=zeros(n);
P1=E;
for k=1:n-1
%构造w,使Pk=I-2ww'
s=-sign(A(k,k))* norm(A(k:n,k));
R(k,k)=-s;
if k==1
w=[A(1,1)+s,A(2:n,k)']';
else
w=[zeros(1,k-1),A(k,k)+s,A(k+1:n,k)']';
R(1:k-1,k)=A(1:k-1,k);
end
if norm(w)~=0
w=w/norm(w);
end
P=E-2*w*w';
A=P*A;
P1=P*P1;
R(1:n,n)=A(1:n,n);
end
Q=P1';
if nargin==2
b=P1*b;
X(n)=b(n)/R(n,n);
for i=n-1:-1:1
X(i)=(b(i)-sum(R(i,i+1:n).*X(i+1:n)'))/R(i,i);
end
else
X=[];
end
matlab自带方法
%产生一个3*3大小的魔方矩阵
A=magic(3)
[Q,R]=qr(A)
使用Eigen C++ Eigen提供了几种矩阵分解的方法
| 分解方式 | Method | 矩阵满足条件 | 计算速度 | 计算精度 |
|---|---|---|---|---|
| PartialPivLU | partialPivLu() | Invertible | ++ | + |
| FullPivLU | fullPivLu() | None | - | +++ |
| HouseholderQR | householderQr() | None | ++ | + |
| ColPivHouseholderQR | colPivHouseholderQr() | None | + | ++ |
| FullPivHouseholderQR | fullPivHouseholderQr() | None | - | +++ |
| LLT | llt() | Positive definite | +++ | + |
| LDLT | ldlt() | Positive or negative semidefinite | +++ | ++ |
其中HouseholderQR、ColPivHouseholderQR、FullPivHouseholderQR是我们目前要用到的QR分解方法
C++的QR分解代码为
#include
#include
using namespace Eigen;
using namespace std;
int main() {
Matrix3d A;
A<<1,1,1,
2,-1,-1,
2,-4,5;
HouseholderQR qr;
qr.compute(A);
MatrixXd R = qr.matrixQR().triangularView();
MatrixXd Q = qr.householderQ();
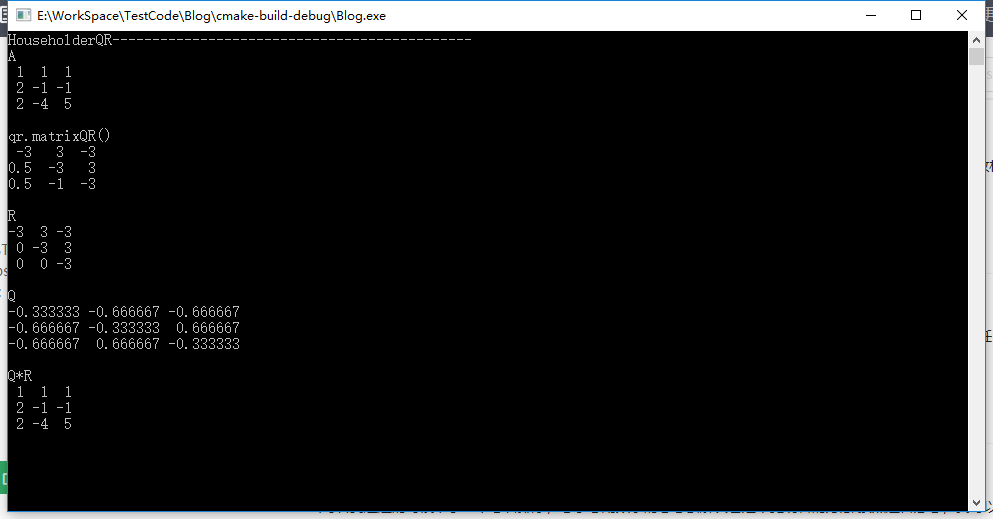
std::cout << "QR2(): HouseholderQR---------------------------------------------"<< std::endl;
std::cout << "A "<< std::endl < 好了大功告成,为什么我要写计算方法的文章呢,虽然现在有很多的库和包给我们调用,但是我们也不能忘了代码的本质是为了解决复杂的数学问题,从根源上去理解一种计算方法有助于我们对自身代码的优化,比如这些方法我们可以把它写到FPGA和CUDA等并行或者分布式的计算当中,加速我们的计算方法,这比直接单机去调用这些库会超乎想象的快。