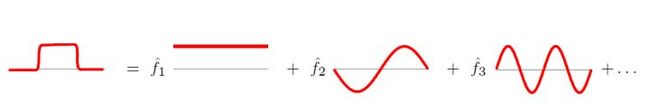图卷积神经网络（Graph Convolutional Network）之谱卷积

本文主要参考了:

• 从CNN到GCN的联系与区别——GCN从入门到精（fang）通（qi）
• Chebyshev多项式作为GCN卷积核
• 拉普拉斯矩阵与拉普拉斯算子的关系

其他见参考文献部分。

1.拉普拉斯矩阵

1.1 简单图的拉普拉斯矩阵

给定一个具有$n$个顶点的简单无向图$G(V,E)$，

• $A$是图$G=(V,E)$的邻接矩阵
• $D$是顶点的度矩阵（对角矩阵），$D_{ii}={\sum }_j{A}_{ij}$
• 拉普拉斯矩阵$L_{n\times n}$为$L=D-A$。

$L$中的元素定义为
$$L_{i,j}=\{\begin{array}{ll}deg(v_i)& \text{if }i=j\\ -1& \text{if }i\ne j\text{and is }{v}_i\text{ adjacent to }{v}_j\\ 0& \text{otherwise}\end{array}$$
其中$deg(v_i)$是顶点$v_i$的度。

可以验证，对于任意的图$G=(V,E)$的顶点$V$上的函数$f\in {\mathbb{R}}^n$都有[14]:
$$\left(\mathcal{L}f\right)(v_i)=\sum _{v_i\sim v_j}{a}_{i,j}\left(f(v_i)-f(v_j)\right).$$
其中$v_i\sim v_j$表示所有与顶点$v_i$相连接的顶点集合，$a_{i,j}$是两顶点$v_i,v_j$之间的连接权重。

1.2 对称归一化拉普拉斯算子

对称归一化拉普拉斯矩阵定义为：
$$L^{sys}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$$
$L^{sys}$中的元素定义为
$$L_{i,j}^{sys}=\{\begin{array}{ll}1& \text{if }i=j\text{ and }deg(v_i)\ne 0\\ -\frac{1}{\sqrt{deg(v_i)deg(v_j)}}& \text{if }i\ne j\text{ nd is }{v}_i\text{ adjacent to }{v}_j\\ 0& \text{otherwise}\end{array}$$

1.3 随机游走归一化拉普拉斯算子

随机游走归一化拉普拉斯矩阵定义为：
$$L^{rw}=D^{-1}L=I_N-D^{-1}A$$

$L^{rw}$中的元素定义为
$$L_{i,j}^{rw}=\{\begin{array}{ll}1& \text{if }i=j\text{ and }deg(v_i)\ne 0\\ -\frac{1}{deg(v_i)}& \text{if }i\ne j\text{ nd is }{v}_i\text{ adjacent to }{v}_j\\ 0& \text{otherwise}\end{array}$$

1.4 拉普拉斯矩阵的基本性质

对于（无向）图$G(V,E)$及其具有特征值的拉普拉斯矩阵$L$，将其特征值排列为${\lambda }_0,{\lambda }_1,\cdots ,{\lambda }_{n-1}$:

• $L$是对称的。
• $L$是半正定的，即${\lambda }_i\ge 0$。
• $L$的每一行和列总和为零。
• $L$是M矩阵[6]。

L矩阵的定义[8]：若$A$一个$n\times n$的方阵，若$a_{ii}>0$, 而$a_{ij}\le 0(i\ne j)$，则称$A$为L矩阵。
M矩阵的定义[8]：若$A$为L矩阵，其为M矩阵的条件为下列之一：

• $A$的所有特征值的实部皆为正。
• $A$的所有主子式皆为正。
• $A$的所有顺序主子式皆为正。
• $A$的逆存在且为非负矩阵。
• 有正向量$x$，使$Ax$为正向量。
• 有对角线主元素全为正的对角形矩阵（叫做正对角形矩阵）$D$，使$ADe$为正向量，其中$e=(1,\cdots ,1{)}^T$。
• 对实向量$x$，若$Ax$非负，则$x$非负。
• 若$D=diag(A),C=D-A,B=D^{-1}\ast C$，则$\rho (B)<1$，其中$\rho (B)$为$B$的特征值的模的最大值。
• $B=\lambda I-A$为非负矩阵，其中$I$为单位矩阵，$\lambda >\rho (B)$。
• 若$B$为$L$矩阵，且$b_{ij}\ge a_{ij},i,j=1,2,\cdots ,n$，则$B$的逆存在。
• 存在下三角矩阵$T$和上三角矩阵$U$，其中$T$和$U$均为L矩阵，使$A=TU$.

1.5拉普拉斯矩阵特征值分解

对$L$特征值分解为
$$L=U\left(\begin{array}{ccc}{\lambda }_0& & \\ & \ddots & \\ & & {\lambda }_{n-1}\end{array}\right)U^{-1}=U\Lambda U^{-1}.$$
其中$U=(u_0,u_1,\cdots ,u_{n-1})$是由$L$的特征向量（列向量）组成的矩阵，相应列的特征向量与特征值矩阵$\Lambda$相应列的特征值相互对应。

由于$U$是正交矩阵，即$U{U}^T=I_n$，即上面的式子又可以写成：
$$L=U\Lambda U^T.$$

2.拉普拉斯算子

2.1拉普拉斯算子的定义[5]

梯度 ： 设$f:{\mathbb{R}}^3\to \mathbb{R}$在空间区域$G$上具有一阶连续偏导数，点$P(x_1,x_2,x_3)\in G$，称向量
$$\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3}\right)=\frac{\partial f}{\partial x_1}{i}_1+\frac{\partial f}{\partial x_2}{i}_2+\frac{\partial f}{\partial x_3}{i}_3$$
为函数$f$在点$P$处的梯度，记作$\nabla f(x_1,x_2,x_3)$或$grad(f)$。

其中
$$\nabla =\frac{\partial }{\partial x_1}{i}_1+\frac{\partial }{\partial x_2}{i}_2+\frac{\partial }{\partial x_3}{i}_3$$
称作（三维）向量的微分算子。多维的则为$\nabla ={\sum }_{j=1}^n\frac{\partial }{\partial x_j}{i}_j$。

散度 散度 "$\nabla .$ " （divergence）可用于表针空间中各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性。当 $div(F)>0$，表示该点有散发通量的正源（发散源）；当$div(F)<0$ 表示该点有吸收能量的负源（洞或汇）；当$div(F)=0$，表示该点无源。

拉普拉斯算子： 拉普拉斯算子（Laplace Operator）是$n$维欧几里得空间中的一个二阶微分算子，定义为梯度（ $\nabla f$ ）的散度（ $\nabla .$ ）。$\Delta f={\nabla }^{2}f=\nabla .\nabla f=div(grad(f))$。

笛卡尔坐标系下的表示法：
$$\Delta f=\frac{{\partial }^{2}f}{\partial x_1^2}+\frac{{\partial }^{2}f}{\partial x_2^2}+\frac{{\partial }^{2}f}{\partial x_3^2}$$
$n$维时为$\Delta ={\sum }_i\frac{{\partial }^{2}f}{\partial x_i^2}$。

2.2离散拉普拉斯算子

在离散的情况下，$\frac{\partial f}{\partial x}=f^{{}^{\prime }}(x)=f(x+1)-f(x)$，
则
$$\begin{array}{rl}\frac{{\partial }^{2}f}{\partial x^2}& =f^{{}^{\prime \prime }}(x)\approx f^{{}^{\prime }}(x)-f^{{}^{\prime }}(x-1)\\ & =f(x+1)+f(x-1)-2f(x).\end{array}$$

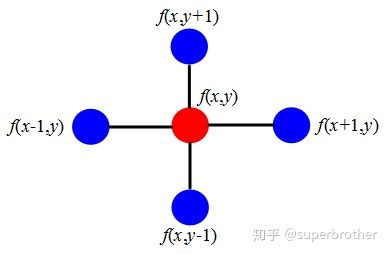
以二维情况为例子，见下图：

$$\begin{array}{rl}\Delta f& =\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}\\ & =\left(f(x+1,y)+f(x-1,y)-2f(x,y)\right)+\left(f(x,y+1)+f(x,y-1)-2f(x,y)\right)\\ & =f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)\end{array}$$

现在用散度的概念解读一下：

• 如果 $\Delta f=0$ ，可以近似认为中心点 $f(x,y)$ 的势和其周围点的势是相等的， $f(x,y)$局部范围内不存在势差。所以该点无源
• $\Delta f>0$ ，可以近似认为中心点$f(x,y)$的势低于周围点，可以想象成中心点如恒星一样发出能量，补给周围的点，所以该点是正源
• $\Delta f<0$ ,可以近似认为中心点$f(x,y)$的势高于周围点，可以想象成中心点如吸引子一样在吸收能量，所以该点是负源

另一个角度，拉普拉斯算子计算了周围点与中心点的梯度差。当$f(x,y)$受到扰动之后，其可能变为相邻的$f(x+1,y),f(x-1,y),f(x,y+1),f(x,y-1)$之一，拉普拉斯算子得到的是对该点进行微小扰动后可能获得的总增益 （或者说是总变化）。

2.3图上的拉普拉斯算子

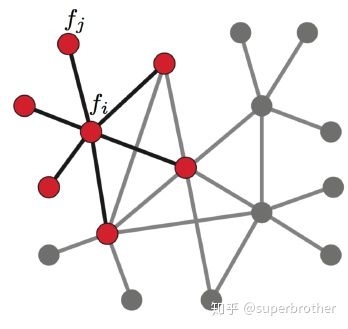
现在将这个结论推广到图： 假设具有$N$个节点的图$G$，此时以上定义的函数$f$不再是二维，而是$N$维向量：$f=(f_1,f_2,\cdots ,f_N)$ ，其中$f_i$为函数$f$在图中节点$v_i$处的函数值。类比于$f(x,y)$在节点$(x,y)$处的值。对$v_i$节点进行扰动，它可能变为任意一个与它相邻的节点$v_j\in N_i$, $N_i$表示节点$v_i$的一阶邻域节点。

如下图：

上面已经知道拉普拉斯算子可以计算一个点到它所有自由度上微小扰动的增益，则通过图来表示就是任意一个节点$v_j$变化到节点$v_i$所带来的增益，考虑图中边的权值相等（简单说就是1）则有：
$$\Delta f_i=\sum _{v_j\in N_i}(f_i-f_j).$$
而如果$e_{i,j}$具有权重$a_{ij}$时，则为：
$$\Delta f_i=\sum _{v_j\in N_i}{a}_{ij}(f_i-f_j).$$

上式即为$\left(\mathcal{L}f\right)(v_i)={\sum }_{v_i\sim v_j}{a}_{i,j}\left(f(v_i)-f(v_j)\right)$。

可以看到上面的式子仅限于$v_j\in N_i$（或$v_i\sim v_j$），如果令$a_{ij}=0$表示节点$v_i,v_j$不相连。则可以拓展：
$$\begin{array}{rl}\Delta f_i& =\sum _{v_j\in V}{a}_{ij}(f_i-f_j)\\ & =\sum _{v_j\in V}{a}_{ij}{f}_i-\sum _{v_j\in V}{a}_{ij}{f}_j\\ & =\left(\sum _{v_j\in V}{a}_{ij}\right)f_i-a_{i}f.\end{array}$$
记$d_i={\sum }_{v_j\in V}{a}_{ij}$是顶点$v_i$的度。

对所有的$N$个节点有：
$$\begin{array}{rl}\Delta f& =\left(\begin{array}{c}\Delta f_1\\ ⋮\\ \Delta f_N\end{array}\right)=\left(\begin{array}{c}{d}_1{f}_1-a_{1}f\\ ⋮\\ d_N{f}_N-a_{N}f\end{array}\right)\\ & =\left(\begin{array}{ccc}{d}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & d_N\end{array}\right)f-\left(\begin{array}{c}{a}_1\\ ⋮\\ a_N\end{array}\right)f\\ & =diag(d_i)f-Af\\ & =(D-A)f\\ & =Lf\end{array}$$

2.4拉普拉斯算子与拉普拉斯矩阵的关系

再次考虑二维情况，离散化的拉普拉斯算子得到的
$$\Delta f=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)$$
与图上拉普拉斯矩阵得到的[14]
$$\left(\mathcal{L}f\right)(x,y)=4f(x,y)-\left(f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)\right)$$
两者只相差一个符号。

3.傅里叶变换

3.1傅里叶变换简要推导[15]

用$e^{\frac{j\pi x}{L}i}$作基，$c_j$作因子，表示函数$f(x)$：
$$f(x)=\sum _{j=-\infty }^{\infty }{c}_j{e}^{\frac{j\pi x}{L}i}.$$
其中的因子$c_j$为：
$$c_j=\frac{1}{2L}{\int }_{-L}^{L}f(t)e^{-\frac{j\pi t}{L}i}dt,-\infty <j<\infty .$$
将因子代入有：
$$f(x)=\sum _{j=-\infty }^{\infty }\left[\frac{1}{2L}{\int }_{-L}^{L}f(t)e^{-\frac{j\pi t}{L}i}dt\right]e^{\frac{j\pi x}{L}i}.$$
令${\xi }_j=\frac{\pi j}{L},\Delta \xi =\frac{\pi }{L}$，上面二式改写成：
$$\begin{array}{rl}{F}_L(\xi )& =\frac{1}{2\pi }{\int }_{-L}^{L}f(t)e^{-i\xi t}dt\\ f(x)& =\sum _{j=-\infty }^{\infty }{F}_L({\xi }_j)e^{i\xi t}\Delta \xi .\end{array}$$
令$L\to \infty$，将黎曼和转为积分则：
$$\begin{array}{rl}f(x)& ={\int }_{j=-\infty }^{\infty }\left[\frac{1}{2\pi }{\int }_{-\infty }^{\infty }f(t)e^{-i\xi t}dt\right]e^{i\xi t}d\xi .\\ & =\frac{1}{\sqrt{2\pi }}{\int }_{j=-\infty }^{\infty }\left[\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f(t)e^{-i\xi t}dt\right]e^{i\xi t}d\xi .\end{array}$$

得到傅里叶变换及其逆变换：
$$\begin{array}{rl}\hat{f}(\xi )& =\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f(t)e^{-i\xi t}dt\\ f(x)& =\frac{1}{\sqrt{2\pi }}{\int }_{j=-\infty }^{\infty }\hat{f}(\xi )e^{i\xi t}d\xi .\end{array}$$

3.2离散傅里叶变换[15]

在连续的情况中，因子$c_j$为：
$$c_j=\frac{1}{2\pi }{\int }_0^{2\pi }f(t)e^{-ijx}dt,-\infty <j<\infty .$$
将其离散化：
$$c_j\approx \frac{1}{n}\sum _{k=0}^{n-1}f(x_k)e^{ij{x}_k}.$$
类比，得到离散的傅里叶变换：
$${\hat{y}}_k=\sum _{j=0}^{n-1}{w}_n^{-kj}{y}_j,0\le k\le n-1,$$
其中$w_n=e^{\frac{2\pi i}{n}}$。

将其写成矩阵形式：
$$\left(\begin{array}{c}{\hat{y}}_0\\ {\hat{y}}_1\\ {\hat{y}}_2\\ ⋮\\ {\hat{y}}_{n-1}\end{array}\right)=\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& w_n^{-1}& w_n^{-2}& \cdots & w_n^{-(n-1)}\\ 1& w_n^{-2}& w_n^{-4}& \cdots & w_n^{-2(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& w_n^{-(n-1))}& w_n^{-(n-1)}& \cdots & w_n^{-(n-1{)}^2}\end{array}\right)\left(\begin{array}{c}{y}_0\\ y_1\\ y_2\\ ⋮\\ y_{n-1}\end{array}\right).$$
记
$$F_n=\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& w_n^1& w_n^2& \cdots & w_n^{(n-1)}\\ 1& w_n^2& w_n^4& \cdots & w_n^{2(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& w_n^{(n-1))}& w_n^{(n-1)}& \cdots & w_n^{(n-1{)}^2}\end{array}\right).$$
即离散傅里叶变换为:
$$\hat{y}=\overline{F_n}y.$$

根据
$$(\overline{F_n}{)}^{-1}=\frac{1}{n}{F}_n,$$
得到逆离散傅里叶变换为:
$$y=\frac{1}{n}{F}_n\hat{y}.$$

3.3图上傅里叶变换

在傅里叶变换中，使用的基函数$e^{-iwt}$是因为它是拉普拉斯算子的特征函数（满足特征方程）, $w$就和特征值有关。

广义的特征方程定义为：
$$AV=\lambda V$$
其中$A$是一种变换，$V$是特征向量或者特征函数（无穷维的向量），$\lambda$是特征值。

$e^{-iwt}$满足：
$$\Delta e^{-iwt}=\frac{{\partial }^2}{{\partial }^{2}t}{e}^{-iwt}=-w^2{e}^{-iwt}.$$
当然$e^{-iwt}$就是变换$\Delta$的特征函数，$w$和特征值密切相关。

$L$是拉普拉斯矩阵，$V$是其特征向量，自然满足下式：
$$LV=\lambda V.$$

由此得到图上的傅里叶变换：
$$\mathcal{F}[f({\lambda }_l)]=\hat{f}({\lambda }_l)=⟨f,u_l⟩=\sum _{v_i\in V}f(v_i)u_l^{\ast }(v_i)$$
矩阵形式为:
$$\begin{array}{rlr}& \text{图上傅里叶变换： }& \hat{f}=U^{T}f\\ & \text{图上逆傅里叶变换： }& f=U\hat{f}\end{array}$$

3.4为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基？特征值表示频率？

3.4.1为什么拉普拉斯矩阵的特征向量可以作为傅里叶变换的基？

傅里叶变换一个本质理解就是：把任意一个函数表示成了若干个正交函数（由sin,cos 构成）的线性组合。

图上傅里叶变换也把图上定义的任意向量$f$，表示成了拉普拉斯矩阵特征向量的线性组合，即：
$$f=\sum _{i=0}^{n-1}\hat{f}({\lambda }_0)u_0.$$

为什么graph上任意的向量$f$都可以表示成这样的线性组合？
原因是，$u_0,u_1,\cdots ,u_{n-1}$是图上$n$维空间中的$n$个线性无关的正交向量。

3.4.2怎么理解拉普拉斯矩阵的特征值表示频率？

在图空间上无法可视化展示“频率”这个概念，那么从特征方程上来抽象理解。

因为$L{1}_{n\times 1}=0_{n\times 1}$可知$L$的最小特征值${\lambda }_0=0$。

从特征方程的数学理解来看：
$$Lu=\lambda u.$$
在由图确定的$n$维空间中，越小的特征值${\lambda }_l$表明：拉普拉斯矩阵$L$其所对应的基$u_l$上的分量、“信息”越少，那么当然就是可以忽略的低频部分了。

其实图像压缩就是这个原理，把像素矩阵特征分解后，把小的特征值（低频部分）全部变成0，PCA降维也是同样的，把协方差矩阵特征分解后，按从大到小取出前K个特征值对应的特征向量作为新的“坐标轴”。

4.GCN卷积

4.1图上卷积

卷积定理[7] ：
$$\mathcal{F}\left[f_1(t)\star f_2(t)\right]=\mathcal{F}\left[f_1(t)\right]\odot \mathcal{F}\left[f_2(t)\right]$$
其中$\star$为卷积运算符，$\odot$表示Hadamard product（哈达马积），对于两个维度相同的向量、矩阵、张量进行对应位置的逐元素乘积运算。

卷积定理将卷积与傅里叶变换联系起来。由此我们得到了图上的卷积：
$${\left(f\star h\right)}_G=U\left[\left(U^{T}h\right)\odot \left(U^{T}f\right)\right].$$

这里为了后续说明问题的方便，不再使用$\odot$。两向量$U^{T}h,U^{T}f$做逐点乘积，等价于把其中一个向量对角化做矩阵乘积：
$$\begin{array}{rl}\left(U^{T}h\right)\odot \left(U^{T}f\right)& =\left(\begin{array}{c}\hat{h}({\lambda }_0)\\ \hat{h}({\lambda }_1)\\ ⋮\\ \hat{h}({\lambda }_{n-1})\end{array}\right)\odot \left(\begin{array}{c}\hat{f}({\lambda }_0)\\ \hat{f}({\lambda }_1)\\ ⋮\\ \hat{f}({\lambda }_{n-1})\end{array}\right)\\ & =\left(\begin{array}{cccc}\hat{h}({\lambda }_0)& & & \\ & \hat{h}({\lambda }_1)& & \\ & & \ddots & \\ & & & \hat{h}({\lambda }_{n-1})\end{array}\right)\left(\begin{array}{c}\hat{f}({\lambda }_0)\\ \hat{f}({\lambda }_1)\\ ⋮\\ \hat{f}({\lambda }_{n-1})\end{array}\right)\\ & =diag(\hat{h}({\lambda }_l))U^{T}f.\end{array}$$

因此用矩阵形式：
$${\left(f\star h\right)}_G=U\left(\begin{array}{cccc}\hat{h}({\lambda }_0)& & & \\ & \hat{h}({\lambda }_1)& & \\ & & \ddots & \\ & & & \hat{h}({\lambda }_{n-1})\end{array}\right)U^{T}f=Udiag(\hat{h}({\lambda }_l))U^{T}f.$$

4.2第一代GCN

Spectral Networks and Locally Connected Networks on Graphs中简单粗暴地把$diag(\hat{h}({\lambda }_l))$变成卷积核$diag({\theta }_l)$，即：
$$y_{out}=\sigma \left(U{g}_{\theta }(\Lambda )U^T{x}_{in}\right).$$

其中$\sigma (.)$是激活函数，卷积核$g_{\theta }(\Lambda )$为
$$g_{\theta }(\Lambda )=\left(\begin{array}{ccc}{\theta }_0& & \\ & \ddots & \\ & & {\theta }_{n-1}\end{array}\right).$$

第一代的参数方法存在着一些弊端：主要在于：

• 每次前向传播需要计算$U,diag({\theta }_l),U^T$三者的矩阵乘积，计算复杂度为$\mathcal{O}(n^2)$。
• 卷积核不具有spatial localization。
• 卷积核需要$n$个参数。

4.3第二代GCN

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering把$\hat{h}({\lambda }_l)$巧妙地设计成了${\sum }_{j=0}^K{\alpha }_j{\lambda }_l^j$，即：
$$\begin{array}{rl}{g}_{\theta }(\Lambda )& =\left(\begin{array}{ccc}{\sum }_{j=0}^K{\alpha }_j{\lambda }_0^j& & \\ & \ddots & \\ & & {\sum }_{j=0}^K{\alpha }_j{\lambda }_{n-l}^j\end{array}\right)\\ & =\sum _{j=0}^K\left[{\alpha }_j\left(\begin{array}{ccc}{\lambda }_0^j& & \\ & \ddots & \\ & & {\lambda }_{n-l}^j\end{array}\right)\right]\\ & =\sum _{j=0}^K{\alpha }_j{\Lambda }^j.\end{array}$$
利用拉普拉斯矩阵特征值分解的性质$L^2=U\Lambda U^{T}U\Lambda U^T=U{\Lambda }^2{U}^T$,进而有:
$$\begin{array}{rl}U{g}_{\theta }(\Lambda )U^T& =U\left(\sum _{j=0}^K{\alpha }_j{\Lambda }^j\right)U^T\\ & =\sum _{j=0}^K\left({\alpha }_{j}U{\Lambda }^j{U}^T\right)\\ & =\sum _{j=0}^K{\alpha }_j{L}^j.\end{array}$$

卷积层为：
$$y_{out}=\sigma \left(U{g}_{\theta }(\Lambda )U^T{x}_{in}\right)=\sigma \left(\sum _{j=0}^K{\alpha }_j{L}^j{x}_{in}\right).$$

第二代卷积核其优点在于在于：

• 卷积核只需要$K$个参数$({\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_{n-1})$，一般$K$远小于$n$。
• 不需要再做特征值分解了。计算机复杂仍然是$\mathcal{O}(n^2)$。
• 卷积核具有很好的spatial localization。特别地，$K$就是卷积核的receptive field，也就是说每次卷积会将中心顶点K-hop neighbor上的feature进行加权求和，权系数就是${\alpha }_k$。

4.4利用Chebyshev多项式作为卷积核[12]

4.4.1Chebyshev多项式性质

• 递归定义$T_k(y)=2y{T}_{k-1}(y)-T_{k-2}(y)$
• $T_0=1,t_1=y$
• $y\in [-1,1]$
• $T_k(y)=\cos \left(k\arccos (y)\right)$
  $${\int }_{-1}^1\frac{T_l(y)T_m(y)}{\sqrt{1-y^2}}dy=\{\begin{array}{ll}\frac{\pi }{2}{\delta }_{l.m}& \text{if }m,l>0\\ \pi & \text{if }m=l=0.\end{array}$$

Every $h\in L^2([-1,1],\frac{dy}{\sqrt{1-y^2}})$ has a convergent (in $L^2$ norm) Chebyshev series
$$h(y)=\frac{1}{2}{c}_0+\sum _{k=1}^{\infty }{c}_k{T}_k(y)$$
with Chebyshev coefficients
$$c_k=\frac{2}{\pi }{\int }_{-1}^1\frac{T_l(y)T_m(y)}{\sqrt{1-y^2}}dy=\frac{2}{\pi }{\int }_0^{\pi }\cos (k\theta )h(\cos (\theta ))d\theta .$$

4.4.2 Chebyshev多项式卷积核

将$g_{\theta }(\Lambda )$用Chebyshev多项式$T_k(x)$逼近:
$$g_{{\theta }^{{}^{\prime }}}(\Lambda )\approx \sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\tilde{\Lambda }),\tilde{\Lambda }=\frac{2}{{\lambda }_{max}(\Lambda )}\Lambda -I_n$$

由$T_k(y)=\cos \left(k\arccos (y)\right)$可以知道Chebyshev多项式的输入必须是在$[-1,1]$之间，所以需要将$\Lambda$做变换为$\tilde{\Lambda }$。

因此得到Chebyshev多项式逼近图上谱卷积为：
$$\begin{array}{rl}{g}_{{\theta }^{{}^{\prime }}}\star x& \approx U\left(\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\tilde{\Lambda })\right)U^{T}x\\ & =\sum _{k=0}^K\left(U{\theta }_k^{{}^{\prime }}{T}_k(\tilde{\Lambda })U^T\right)x\\ & =\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k\left(U\tilde{\Lambda }{U}^T\right))x\\ & =\sum _{k=0}^K{\theta }_k^{{}^{\prime }}{T}_k(\tilde{L})x\end{array}$$
其中$\tilde{L}=\frac{2}{{\lambda }_{max}(L)}L-I_N$。

4.5 Chebyshev多项式逼近法简化[9,10]

如果取${\lambda }_{max}\approx 2$则有$\tilde{L}=L-I_N$。Chebyshev多项式只取前两项，即$K=1$ 有
$$\begin{array}{rl}{g}_{{\theta }^{{}^{\prime }}}\star x& \approx \left({\theta }_0^{{}^{\prime }}+{\theta }_1^{{}^{\prime }}(L-I_N)\right)x\\ & =\left({\theta }_0^{{}^{\prime }}-{\theta }_1^{{}^{\prime }}{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x\end{array}.$$

4.6 单参数法[9,10]

令参数${\theta }_0^{{}^{\prime }}=-{\theta }_1^{{}^{\prime }}=\theta$，图上谱卷积又可以简化为
$$g_{{\theta }^{{}^{\prime }}}\star x\approx \theta \left(I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x$$

注意$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$拥有范围为$[0,2]$的特征值，这将会导致数值不稳定性和梯度爆炸/消失。因此我们介绍下面的归一化技巧(renormalization trick)：
$$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}.$$
其中$\tilde{A}=A+I_N,{\tilde{D}}_{i,i}={\sum }_j{\tilde{A}}_{i,j}={\sum }_j\left(A_{i,j}+(I_N{)}_{i,j}\right)=D_{i,i}+1$。上式展开为
$$\begin{array}{rl}{I}_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}& \to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}\\ & =(D+I_N{)}^{-\frac{1}{2}}(A+I_N)(D+I_N{)}^{-\frac{1}{2}}\\ & =(D+I_N{)}^{-\frac{1}{2}}A(D+I_N{)}^{-\frac{1}{2}}+(D+I_N{)}^{-1}\end{array}.$$

输入$X\in {\mathbb{R}}^{N\times C}$，$C$为输入的通道数，经过滤波$\Theta \in {\mathbb{R}}^{C\times F}$得到含有$F$个通道的卷积后结果$Z\in {\mathbb{R}}^{N\times F}$：
$$Z={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X\Theta$$

参考文献

• [1] 从CNN到GCN的联系与区别——GCN从入门到精（fang）通（qi）
• [2] Chebyshev多项式作为GCN卷积核
• [3] 解读三种经典GCN中的Parameter Sharing
• [4] 【其实贼简单】拉普拉斯算子和拉普拉斯矩阵
• [5] 拉普拉斯矩阵与拉普拉斯算子的关系
• [6] 图卷积神经网络(GCN)详解:包括了数学基础(傅里叶，拉普拉斯)
• [7] 卷积定理
• [8] M矩阵
• [9] 【GCN】论文笔记：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
• [10] 机器学习论文笔记-Semi-Supervised Classification with Graph Convolutional Networks
• [11] Spectral Networks and Locally Connected Networks on Graphs
• [12] Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
• [13] The Emerging Field of Signal Processing on Graphs
• [14] Wavelets on graphs via spectral graph theory
• [15] Weimin HanKendall,E. Atkinson.Theoretical Numerical Analysis A Functional Analysis Framework Third Edition[M].Springer:New York,2009:167.