理解前向传播、反向传播(Backward Propagation,BP)
文章目录
- 前向传播
- 反向传播
- 一个复杂的例子
- Patterns in Backward Flow
- 神经网络中的 BP 算法
BP 算法是一种参数学习方法,一般分为两个过程:前向传播(求误差),反向传播(误差回传)。
那么什么是前向传播、反向传播呢?这里先说结论:前向传播是为反向传播准备好要用到的数值,反向传播本质上是一种求梯度的高效方法。
求梯度是为了什么呢?就是为了更新模型的参数(权重 W 和偏置 b)。
所有参数值随机初始化(论文乱写一通),前向传播(提交论文),误差函数(审稿),反向传播(审稿人:你这不行,改!),参数更新(修改论文),前向传播,…;反反复复,论文发表(模型训练完毕)。
前向传播
在正式介绍前向传播前,先简单介绍计算图(Computational Graph)的概念,以 y = w ∗ x + b y=w*x+b y=w∗x+b 可以用下面的有向无环图表示。
再简单说下前向传播,如下图(图片来自于 李飞飞 CS231n 2017 的课程),图右上角是 f ( x , y , z ) = ( x + y ) ∗ z f(x, y, z)=(x+y)*z f(x,y,z)=(x+y)∗z 的计算图。
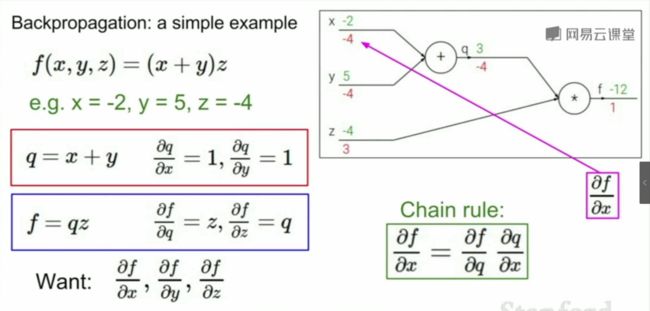
分别赋值 x = − 2 , y = 5 , z = − 4 x = -2,y = 5, z = -4 x=−2,y=5,z=−4,从计算图的左边开始,数据开始流动,依次计算出 q 、 f q、f q、f。
最终得到计算图中那 6 个绿色的数字,这就是前向传播的结果。
文章开头给出的结论:前向传播是为反向传播准备好要用到的数值,反向传播本质上是一种求梯度的高效方法。
反向传播
我们说了,反向传播本质上是一种求梯度的高效方法。
那么什么是梯度(Gradient)?这里简单说下,梯度是一个向量,其指向的方向就是函数上升最快的方向,梯度向量由偏导数构成其各分量。
这里把思路捋一下:求损失函数最小值 → 梯度下降法 → 求梯度 → 求偏导数
那怎么求偏导数呢?学过高数的都知道,求导法则啊!比如说下面这个函数,
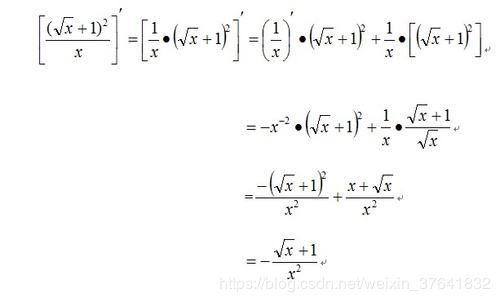
老汤说,这道题我拿到手就会算。可计算机不是人啊,那计算机是怎么做的呢,没错,就是计算图,通过链式法则(Chain Rule)一步步分解复杂函数,逐步求解。
回到前向传播的那个图,

我们要求偏导数 ∂ f ∂ x \frac{\partial f}{\partial x} ∂x∂f,分解为:
∂ f ∂ x = ∂ f ∂ q ⋅ ∂ q ∂ x \frac{\partial f}{\partial x}=\frac{\partial f}{\partial q} \cdot \frac{\partial q}{\partial x} ∂x∂f=∂q∂f⋅∂x∂q
提前说明:计算图中红色的数字是反向传播的结果。最右边的 1 1 1 怎么来的呢, ∂ f ∂ f = 1 \frac{\partial f}{\partial f}=1 ∂f∂f=1
我们再对 f f f 求关于 q q q 的偏导, ∂ f ∂ q = z = − 4 \frac{\partial f}{\partial q}=z=-4 ∂q∂f=z=−4
再对 q q q 求关于 x x x 的偏导, ∂ q ∂ x = 1 \frac{\partial q}{\partial x}=1 ∂x∂q=1
其他的不再赘述。
文章开头给出的结论:前向传播是为反向传播准备好要用到的数值,反向传播本质上是一种求梯度的高效方法。
这里也就不难理解了,反向传播其实就是将复杂函数(尽管例子中的函数并不复杂)的求导,分解成一个个小步骤。
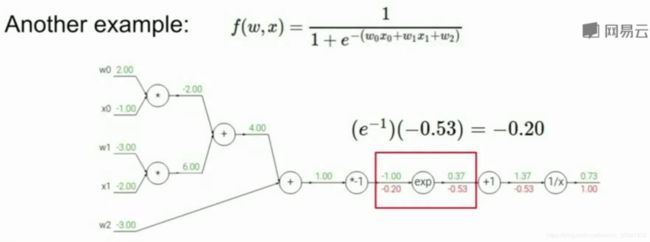
一个复杂的例子
讲师 Serena Yeung 在课堂上给出了一个更复杂的例子,▲▼ 传送门 ▼▲。
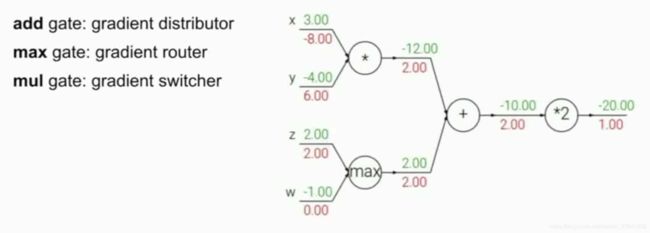
Patterns in Backward Flow
这里讨论计算图中不同函数结点(function node)的作用。
a d d g a t e add \ gate add gate:获取上游梯度(upstream gradient),不改变任何值,传递分发给相连的分支
m a x g a t e max\ gate max gate:获取上游梯度(upstream gradient),原值传递给相连的最大分支,〇传递给相连的最大分支外的其他分支
m u l g a t e mul\ gate mul gate:获取上游梯度 2.00 2.00 2.00,则 − 8.00 = − 4.00 ∗ 2.00 -8.00 = -4.00 * 2.00 −8.00=−4.00∗2.00, 6.00 = 3.00 ∗ 2.00 6.00 = 3.00 * 2.00 6.00=3.00∗2.00
神经网络中的 BP 算法
神经网络中的 BP 和计算图的差不多,(其实就是把神经网络的结构转换成计算图…)
事实上,上一个例子中的 Sigmoid 函数(逻辑回归)可以看成一个简单的浅层网络。
balabala…
神经网络本质上都是矩阵运算:矩阵乘法、矩阵相加、矩阵求导等。
神经网络中的 BP 算法的过程看这里吧。
更细节:神经网络,BP算法的理解与推导 - 折射的文章 - 知乎